Copyright © 1998 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1988. 36:
539-598 Copyright © 1998 by Annual Reviews. All rights reserved |
4.4. Nonlinear Evolution of Jet Dynamics
The numerical approach to the study of jet dynamics
is an approximation of the real physical situations. In fact, although
numerical simulations have become very sophisticated owing to
supercomputers, nevertheless,
the solution of the set of Navier-Stokes or Euler plus Maxwell equations
is still limited to relatively low Reynolds numbers (high viscosity)
R e  100 owing to the discretization process by finite difference schemes. On
the other hand, laboratory experiments indicate that for highly supersonic
jets above these values of Re, the physics does not change
appreciably from the phenomenological point of view.
100 owing to the discretization process by finite difference schemes. On
the other hand, laboratory experiments indicate that for highly supersonic
jets above these values of Re, the physics does not change
appreciably from the phenomenological point of view.
HYDRODYNAMIC SIMULATIONS
Temporal analysis Early simulations of the evolution of
instabilities in cylindrical or slab symmetry were presented by
Hardee & Norman
(1988) but were rather limited in time.
Bodo et al (1994,
1995),
Basset & Woodward
(1995)
have followed the evolution of unstable modes in infinite 2.5-D cylindrical
jets and 2-D slabs. By applying periodic boundary conditions at the initial
and final cross sections of the jet at the extremes of the integration
domain, they simulated the evolution of local perturbations of
wavelengths shorter than the domain length in an infinite flow. This is
called a temporal analysis of the instability. In this way, the
instability can be followed to see whether
nonlinear saturation effects yield to the onset of a quasistationary state.
Bodo et al (1994),
following an exploration of the relevant parameters, i.e. density
contrast  =
=
 ext
/
ext
/  j
and Mach number Mj, determined that jets, after a time
t ~ 30Rj / cs, reach a
quasistationary highly turbulent configuration. Heavy jets
maintain a coherent directionality; light jets appear completely mixed and
diffused. In conclusion, the persistence of jets depends principally on the
density contrast with the ambient medium. Examples of the evolution are
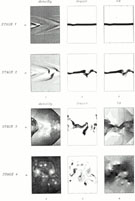
illustrated in Figure 5a, b.
j
and Mach number Mj, determined that jets, after a time
t ~ 30Rj / cs, reach a
quasistationary highly turbulent configuration. Heavy jets
maintain a coherent directionality; light jets appear completely mixed and
diffused. In conclusion, the persistence of jets depends principally on the
density contrast with the ambient medium. Examples of the evolution are
illustrated in Figure 5a, b.
The situation changes drastically in 3-D simulations of cylindrical jets (Bodo et al 1998). Mixing starts much earlier owing to the more rapid growth of small-scale structures, and this is particularly evident in light jets, where fluting modes are present in the linear phase with growth rates that are already larger than those of helical modes. Light jets are asymptotically disrupted by a strong transition to turbulence. Dense jets survive as collimated structures, although the energy and momentum lost by entrainment is larger and the process occurs faster, over time scales of t ~ 10Rj / cs. The final flow velocity also is reduced, and the jet cross section is broadened, as is consistent with strong mass entrainment, which can reach the same load of the jet mass (see Figure 5c).
The physical reason for the instability enhancement in 3-D geometry is the faster development of small-scale structures independently from the initial perturbation. These can be either excited directly, owing to the large growth rate of nonaxisymmetric 3-D modes, or indirectly, through the nonlinear turbulent cascade of energy from large- to small-scale eddies. Another effect that appears to be important in this respect is the different scaling of volumes that makes 3-D jets more expanded.
On the other hand, recent numerical results appear to confirm a result of linear calculations, which shows that the presence of an extended layer around the jet can stabilize the flow by suppressing perturbations with scales smaller than the transverse dimension of the layer. As we discuss in the next section, the formation of layers is admissible under the form of a cocoon produced by the bow shock of the advancing head of the jet or to nonlinear fluid effects at the flow boundary.
Spatial analysis In a different numerical approach, the flow is considered as a finite window on an infinite jet with free boundary conditions at the extremes of the integration domain, and perturbations are produced at the injection nozzle. These perturbations are then followed in their spatial growth while crossing the integration domain and passing through a still undisturbed medium. In this way, nonlinear spatial effects can be analyzed as, for instance, the interaction and merging of shocks along the jet (Norman et al 1988, Micono et al 1998).
The nonlinear evolution of spatial axisymmetric perturbations in 2-D cylindrical and slab structures essentially agrees with the temporal analysis in its initial three stages. The axisymmetric perturbation that dominates eventually is the first reflected mode that actually has the fastest spatial growth rate. A tendency is observed of coalescence of successive shocks into an almost transverse single strong shock that extends into the external medium through entrainment and momentum dissipation.
 |
 |
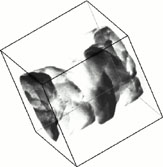 |
Figure 5. Long-term evolution of
Kelvin-Helmholtz instabilities
(Bodo et al 1994,
1995,
1998):
(a) the four phases of evolution in a slab (M = 5,
|
Antisymmetric perturbations in cylindrical jets or nonaxisymmetric perturbations in slabs instead create piston-like protrusions (spurs) into the external medium that travel along the integration grid. They can never reach the quasistationary stage because the spur amplitude becomes very large while travelling along the jet and in fact disrupts the ordered flow (Norman et al 1988, Micono et al 1998). In addition, longitudinal filamentary structures develop that can wrap around the jet if rotation is included in the calculations (Hardee & Stone 1997).
Cooling jets A crucial question is whether radiative losses can affect the global evolution of the instability. In most 2-D cases, even when counteracted by heating, they slow down the growth of instability (Rossi et al 1997, Stone et al 1997, Micono et al 1998). In cylindrical geometry, thermal losses (a case that best applies to stellar jets) are very efficient in suppressing mixing of the jet matter with the external medium, and subsequently matter entrainment. Shocks remain well separated and maintain the characteristic zigzag pattern. However, mixing is present in dense jets. For a slab, mixing and shock coalescence develop on short time scales, and the growth of the instability may in fact be faster. In the case of synchrotron losses, which are more appropriate to extragalactic jets, in addition to Kelvin-Helmholtz-type instabilities, filamentation modes related to thermal-type instabilities are most important and modulate the jets longitudinally (Rossi et al 1993). In fully 3-D geometries that are characterized by faster growth of the instability, radiation losses appear to be too slow and unable to stop the disruption of jets.
MHD SIMULATIONS From a historical point of view, we recall that a 2-D MHD particle code was used by Tajima & Leboeuf (1980) to study Kelvin-Helmholtz instabilities of a single shear layer parallel to a uniform magnetic field but did not reach long time scales of evolution. The numerical analysis of nonlinear MHD instabilities is still limited to rather simple configurations. Most experiments performed so far have used the standard finite difference scheme with finite cells and, correspondingly, a rather large numerical viscosity. Shibata & Uchida (1986) used an evolved Lax-Wendroff scheme. Stone, Norman, and collaborators (Stone & Norman 1992, 1994) developed a 2-D MHD code named ZEUS that is partly based on a higher-order upwind integration scheme. An extension of this last code to a 3-D case is now available but has low resolution for studying the formation of vortices and turbulence. As a consequence, these simulations tend to smooth out strong instabilities and discontinuities.
Recently, Zachary et al (1994) have succeeded in producing a 2-D MHD code with parabolic upwind integration along the characteristics across discontinuities. This MHD Godunov code has been tested on the standard problem of the Kelvin-Helmholtz instability of a shear layer in the case cA < cs (large magnetic fields suppress the instability) (Malagoli et al 1996); the formation of cats' eyes has been followed, and the subsequent series of reconnection events asymptotically yields a stationary turbulent thick layer (Figure 6). A relatively small magnetic field, well below equipartition, helps the shear layer reach a stationary state in which the two fluids in relative motion are separated by a turbulent boundary sheath that eliminates direct interaction. Thus, reconnection seems to be the crucial physical process in governing the magnetic instability evolution. Similar results have been obtained by Frank et al (1996), Min (1997) using an FCT code.
 |
Figure 6. Numerical simulation of a reconnection event (Malagoli et al 1996). |
SHOCKS We conclude discussing in more detail the evolution of "internal shocks" already predicted in linear studies but now properly followed by numerical methods. These shocks arise in the form of conical structures inside a cylindrical jet with typical opening angles of ~ 1 / Mj. The repetitive pattern of oblique shocks is a typical feature of the nonlinear evolution of jets. All these shocks travel with the flow at a velocity slightly below the jet velocity and may be related, as shown in Section 6, to emission morphologies. The intersection points of shocks correspond to high pressure regions with strong emission. Actually, as shown by Hardee & Norman (1989), the merging of shocks gives rise to phase effects where the intersection points can move at a velocity higher than the jet's. This is clearly relevant to the interpretation of superluminal motions in relativistic jets. In later stages, owing to mass entrainment and momentum diffusion, shocks extend at large distances into the external medium perpendicular to the flow and become substantial transverse structures (Bodo et al 1994).