Inflation and the CMB - C.H. Lineweaver

4.3. Horizon problem

What should our assumptions be about regions of the Universe that have never been in causal contact? If we look as far away as we can in one direction and as far away as we can in the other direction we can ask the question, have those two points (points A and B in Fig. 4) been able to see each other. In the standard big bang model without inflation the answer is no. Their past light cones are the little cones beneath points A and B. Inserting a period of inflation during the early universe has the effect of moving the surface of last scattering up to the line labeled "new surface of last scattering". Points A and B then become points A' and B'. And the apexes of their past light cones are at points A' and B'. These two new light cones have a large degree of intersection. There would have been sufficient time for thermal equilibrium to be established between these two points. Thus, the answer to the question: "Why are two points in opposite sides of the sky at the same temperature?" is, because they have been in causal contact and have reached thermal equilibrium.

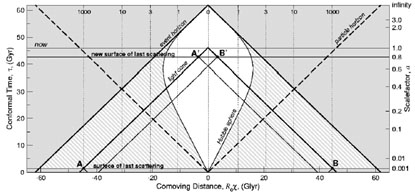Figure 4. Inflation shifts the position of the surface of last scattering. Here we have modified the lower panel of Fig. 1 to show what the insertion of an early period of inflation does to the past light cones of two points, A and B, at the surface of last scattering on opposite sides of the sky. An opaque wall of electrons - the cosmic photosphere, also known as the surface of last scattering - is at a scale factor a = R / R_o approx 0.001 when the Universe was approx 1000 times smaller than it is now and only 380, 000 years old. The past light cones of A and B do not overlap - they have never seen each other - they have never been in causal contact. And yet we observe these points to be at the same temperature. This is the horizon problem (Sect. 4.3). Grafting an early epoch of inflation onto the big bang model moves the surface of last scattering upward to the line labeled "new surface of last scattering". Points A and B move upward to A' and B'. Their new past light cones overlap substantially. They have been in causal contact for a long time. Without inflation there is no overlap. With inflation there is. That is how inflation solves the problem of identical temperatures in `different' horizons. The y axis shows all of time. That is, the range in conformal time [0, 62] Gyr corresponds to the cosmic time range [0, infty ] (conformal time tau is defined by d tau = dt / R). Consequently, there is an upper limit to the size of the observable universe. The isosceles triangle of events within the event horizon are the only events in the Universe that we will ever be able to see - probably a very small fraction of the entire universe. That is, the x axis may extend arbitrarily far in both directions. Like this downarrow .

Figure 5.

Five years ago most of us thought that as we waited patiently we would be rewarded with a view of more and more of the Universe and eventually, we hoped to see the full extent of the inflationary bubble - the size of the patch that inflated to form our Universe. However, Lambda has interrupted these dreams of unfettered empiricism. We now think there is an upper limit to the comoving size of the observable universe. In Fig. 4 we see that the observable universe (= particle horizon) in the new standard Lambda -CDM model approaches 62 billion light years in radius but will never extend further. That is as large as it gets. That is as far as we will ever be able to see. Too bad.