Copyright © 1999 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1999. 37:
127-189 Copyright © 1999 by Annual Reviews. All rights reserved |
3.3. Measuring Weak Shear
In addition to the technical problem of the mass reconstruction algorithm and the redshift distribution of the sources, weak lensing is also sensitive to the accuracy of the measurement of ellipticities of lensed galaxies. The atmosphere has dramatic effects; in particular, the seeing circularizes the innermost part of galaxies which affects the measurements of shapes of faint galaxies (see for example the simulations by Bartelmann 1995c). These issues have been investigated in detail by Bonnet & Mellier (1995), Mould et al (1994), Kaiser et al (1995), Van Waerbeke et al (1997). Atmospheric effects (seeing, atmospheric refraction, atmospheric dispersion), telescope handling (flexures of the telescopes, bad guiding) and optical distortions are extrinsic problems that can bias the measurements, though in principle they can be corrected in various ways. The atmospheric dispersion can be minimized by using an I-band filter and by observing clusters close to zenith, which also minimizes the flexures. Optical distortions can be corrected either analytically, if the optics are known perfectly, or by using the stars located in the fields. On the other hand, the ellipticity distribution of the galaxies is an intrinsic source of noise.
The extrinsic and intrinsic noises compete together: the circularization
by the seeing is important only for the faint galaxies because their
typical size is of the same order as the seeing disk. So, in principle
it should be better to use only large (bright) galaxies, though they are
not as numerous as the small (faint) galaxies. On the other hand, the noise
produced by the intrinsic ellipticity distribution of the
galaxies is minimized by averaging the shape of a large number of
galaxies. The typical scale on which galaxies can be averaged is defined
by the spatial resolution of the reconstructed mass map. For intermediate
and high-redshift clusters of galaxies
the typical angular scale is a few arcminutes, so that galaxies must be
averaged on less than one arcminute in order to map the projected
mass-density with a good sampling. If we assume an ellipticity dispersion,

 of about 0.3,
as it is suggested by nearby surveys
and the distribution of galaxies in the Hubble Deep Field (HDF), then we
can measure an ellipticity,
of about 0.3,
as it is suggested by nearby surveys
and the distribution of galaxies in the Hubble Deep Field (HDF), then we
can measure an ellipticity,
 , produced by a
gravitational shear
of |
, produced by a
gravitational shear
of |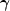 | =
10% if the number of averaged galaxies, N is:
| =
10% if the number of averaged galaxies, N is:
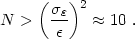 |
(22) |
It is therefore quite easy to measure gravitational shear of 10% on an arcminute scale. However, going down to 1% would require about 900 galaxies which is not feasible on such an angular scale, unless many fields of 1 arcminute are averaged. An alternative is to go deeper in order to increase the galaxy number density. However, this is not sufficient to increase the accuracy of the results, because most of the faint galaxies have an unknown redshift distribution which prevents scaling the mass properly, and also because it is difficult to correct them from PSF.
The procedure to recover the shear field from the ellipticities of individual galaxies has several solutions. Bonnet & Mellier (1995) compute the second moment of galaxies (see Equation 9) within a circular annulus and average the signal on a given area (a superpixel) by using only the faint galaxies that dominate their deep observations. The size of the inner radius is constant and close to the seeing disk, which minimizes the effect of the circularization of the innermost isophotes on the measurement of the ellipse. The outer radius is also constant and has been optimized by using simulations of galaxies in order to get the highest signal-to-noise ratio on each second moment. The drawback of this approach is that the second moment of this annulus is no longer a direct measurement of the shape of the galaxy and it must be calibrated by simulations for each observing condition. The anisotropy of the PSF is corrected on the averaged signal, assuming that it is dominated by optical defects and that it behaves like a stretching of the image. This assumption is not valid for individual galaxies, but for each superpixel, deep observations average so many galaxies that it is possible to assume that the resulting signal reflects the one produced by an ideal galaxy having the same profile on each superpixel. In this case, Bonnet & Mellier have shown from simulations that the correction works very well down to a shear amplitude of 3% (see Bonnet et al 1994, Schneider et al 1998a).
Kaiser et al (1995) (see also Luppino & Kaiser 1997, Hoekstra et al 1998 for further developments) compute the second moment within a variable aperture which depends on the size of individual galaxies; however, instead of an annulus they use a Gaussian filter, and introduce a more rigorous correction of the PSF anisotropy. Because they do not make selection from the size of the galaxies to measure the shear, it is clear that the largest galaxies require less correction. Therefore their correction depends on the total area of each individual galaxy. Assuming that the anisotropy of the PSF is small, Kaiser et al introduced a smearing correction, defined by a linear smear polarizability which expresses the (small) shift of polarization of galaxies induced by an anisotropic PSF. To first order, this shift can be expressed analytically and provides the correction from the shapes of the stars visible in the field, by dividing the smear polarizability by the observed polarization of stars. The efficiency of this method has been tested by using HST images which were degraded to the corresponding PSF anisotropy expected on ground-based images. They proved that the correction works very well. However, the method only works for bright galaxies. For fainter samples, they calibrated the polarization-shear relation by artificially lensing HST images and then by degrading them by the PSF observed in their data. However, it seems more preferable to calibrate the PSF anisotropy directly from the images. Luppino & Kaiser (1997) calibrated the anisotropic correction only from the observations of the stars in their fields, without auxiliary data.
Mould et al (1994) proposed a different procedure: they computed the second moment within a limiting isophote rather than a finite aperture and corrected linearly from the PSF anisotropy, assuming, as did Kaiser et al, that the correction is inversely proportional to the area of the source.
Van Waerbeke et al
(1997) proposed an
original alternative that fully exploits the signal down to the
noise level on each CCD image and reduces the error of the second
moment of galaxies. Instead of using
individual objects, they compute the local auto-correlation function (ACF),
 (
( ), of pixels, averaged on
a given area:
), of pixels, averaged on
a given area:
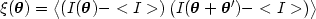 |
(23) |
where < I > is the mean surface brightness
of the area. The (unlensed) ACF of the averaged source population,
 S, is
an isotropic quantity, which by definition
is centered, and therefore does not depend on the detection procedure
and on the computation algorithm of its centroid. When a lensing signal
is present, the shape of the ACF of the lensed population,
S, is
an isotropic quantity, which by definition
is centered, and therefore does not depend on the detection procedure
and on the computation algorithm of its centroid. When a lensing signal
is present, the shape of the ACF of the lensed population,
 I(
I( ) =
) =
 S(A
S(A ) is
no longer isotropic. For example, in the weak lensing regime:
) is
no longer isotropic. For example, in the weak lensing regime:
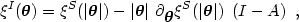 |
(24) |
where I is the identity matrix. The ACF is now composed of the unlensed isotropic component plus an anisotropic term which depends on the magnification matrix, A, which stretches it like a real object. The second moment of the ACF can also be expressed as a function of the distortion and the magnification (Van Waerbeke et al 1997). Because all the pixels of the image are used, the ACF uses the full information of the image; in particular, the flux coming from extremely faint objects, for which the measurement of a centroid and the second moments are not measurable precisely, is also taken into account. For that reason, in principle, the ACF can work on images that reach the confusion limit (Van Waerbeke et al 1997, Réfrégier & Brown 1998). It turns out that in practice it is better to use the ACF around detected galaxies than on the total image because correlated noises, such as electronics cross-talk or shift-and-add residuals, may generate spurious coherent signals (Van Waerbeke & Mellier 1997). This method looks ideal for the optimal extraction of weak lensing signals because the signal-to-noise ratio of the ACF is always high enough and spreads over sufficient pixels to avoid the need for circular filtering, such as faint galaxies, and to provide an accurate estimate of its shape parameters.
The reliability of the relation between measured ellipticities and shear, and of the mass reconstruction obtained from observations, has been checked by Kaiser & Squires (1993), Bonnet & Mellier (1995), and by the independent simulations of Bartelmann (1995c), Wilson et al (1996a). Despite careful studies to check that images are corrected accurately from circularization by seeing and PSF anisotropy (in particular the spatial variation of the PSF in the field can be modeled), there is still a lot of work to do in this area. For instance, the weighting functions proposed to measure the ellipticities are based on intuition but no complete investigation has been done so far to find the optimal one. Moreover, for each of these procedures, it is assumed that the PSF anisotropy is unidirectional. This may not be true, in particular when instruments with poor optical design are used. In that case, the correction becomes non-trivial, and paradoxically this could appear on the image with the best image quality because details of the PSF are no longer smeared by circularization of the seeing. This domain is certainly at its infancy and much work and many new ideas should appear during the next years, mainly because the shear produced by large-scale structures is expected to be very small.