Probing the Universe with Weak Lensing

Annu. Rev. Astron. Astrophys. 1999. 37: 127-189
Copyright © 1999 by Annual Reviews. All rights reserved

3.4. Mass Profile from the Magnification Bias

Parallel to the mass reconstruction using weak shear measurements, one can use the direct measurement of the magnification from the local modification of the galaxy number density. This "magnification bias" expresses the simultaneous effects of the gravitational magnification, which increases the flux received from any lensed galaxies and permits the detection of galaxies enhanced by the amplification, but also magnifies by the same amount the area of the projected lensed sky and thus decreases the apparent galaxy number density. The total amplitude of the magnification bias depends on the slope of the galaxy counts as a function of magnitude and on the magnification factor of the lens. For a circular lens, the radial galaxy number density of background galaxies writes:

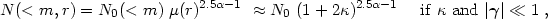$\begin{equation} N(<m,r) = N_0(<m) \ \mu(r)^{2.5\alpha-1} \ \approx N_0 \ (1+2 \kappa)^{2.5\alpha-1} \ \ \ \ {\rm if } \ \kappa\ {\rm and} \ \vert \gammag\vert \ll 1\ , \end{equation}$

(25)

where µ(r) is the magnification, N₀(<m) is the intrinsic (unlensed) number density, obtained from galaxy counts in a nearby empty field, and alpha is the intrinsic count slope:

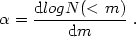$\begin{equation} \alpha = {{\rm d}logN(<m) \over {\rm d}m }\ . \end{equation}$

(26)

A radial magnification bias N(<m,r) shows up only when the slope alpha neq 0.4; otherwise, the increasing number of magnified sources is exactly compensated by the apparent field dilatation. For slopes larger than 0.4 the magnification bias increases the galaxy number density, whereas for slopes smaller than 0.4 the radial density will show a depletion. Hence, no change in the galaxy number density can be observed for B(< 26) galaxies, since the slope is almost this critical value (Tyson 1988). However, it can be detected in the B > 26, R > 24 or I > 24 bands when the slopes are close to 0.3 (Smail et al 1995c).

The change of the galaxy number density can be used as a direct measurement of the magnification and can be included in the maximum likelihood inversion as a direct observable in order to break the mass sheet degeneracy (see Section 3.2). Alternatively, it can also be used to model the lens itself. In the case of a singular isothermal sphere, the magnification can be expressed as a function of the velocity dispersion of the lens, sigma , and the radial distance theta = r / r_E, where r_E = 4 sigma ² / c² D_LS / D_OS:

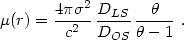$\begin{equation} \mu(r) = {4 \pi \sigma^2 \over c^2}\,{D_{LS} \over D_{OS}}\,{\theta \over \theta-1} \ . \end{equation}$

(27)

Reconstruction of cluster mass distribution using magnification bias was initially explored by Broadhurst et al (1995), and has been used by Taylor et al (1998) in A1689, and by Fort et al (1997) in Cl0024+1654 (see also a generalization by Van Kampen 1998). The masses found are consistent with those inferred from gravitational weak shear or from strong lensing.

This magnification bias is an attractive alternative to the weak shear because it is only based on the galaxy counts and does not require outstanding seeing to measure ellipticities and orientations of galaxies. However, it is more sensitive to shot noise, which unfortunately increases when the number density decreases in the depletion area. Furthermore, it also depends on the galaxy clustering of the background sources which can have large fluctuations from one cluster to another. Indeed, in the weak lensing regime, assuming that kappa approx | gamma |, the ratio of the signal-to-noise ratios of the shear and the depletion, R_Sh/Dep, clearly favors the shear analysis:

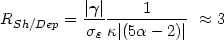$\begin{equation} R_{Sh/Dep}={\vert \gammag \vert \over \sigma_{\varepsilon}} {1 \over \kappa \vert (5 \alpha -2)\vert } \ \approx 3 \end{equation}$

(28)

for a dispersion of the intrinsic ellipticity distribution of the galaxies, sigma = 0.3, and alpha = 0.2. Despite these limitations, this is a simple way to check the consistency of the mass reconstruction. Its great merit is that it is not sensitive to systematic effects, such as the weak shear measurement which depends on the correction from the PSF of the observed ellipticities.