Probing the Universe with Weak Lensing

Annu. Rev. Astron. Astrophys. 1999. 37: 127-189
Copyright © 1999 by Annual Reviews. All rights reserved

3.2. Mass Reconstruction from Weak Lensing

A powerful and complementary way to recover the mass distribution of lenses has been proposed by Kaiser & Squires (1993). It is based on the distribution of weakly lensed galaxies rather than the use of giant arcs. In 1988, Fort et al (1988) obtained at CFHT deep sub-arcsecond images of the lensing-cluster A370 and observed the first weakly distorted galaxies ever detected. The galaxy number density of their observation was about 30 arcmin^-2, mostly composed of background sources, far beyond the cluster. These galaxies lensed by the cluster show a correlated distribution of ellipticity/orientation which maps the projected mass density. The first attempt to use this distribution of arclets as a probe of dark matter was made by Tyson et al (1990), but the theoretical ground and a rigorous inversion technique was first proposed by Kaiser & Squires.

By combining Equations 2, 4, and 5, one can express the complex shear as a function of the convergence, kappa (see Seitz & Schneider 1996 and references therein):

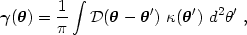$\begin{equation} \gammag(\thetag) = {1 \over \pi} \int \mathcal{D}(\thetag-\thetag') \ \kappa(\thetag') \ d^2\theta' \ , \end{equation}$

(16)

where

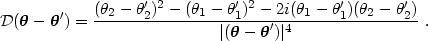$\begin{equation} \mathcal{D}(\thetag-\thetag')={(\theta_2-\theta_2')^2 - (\theta_1-\theta_1')^2- 2i (\theta_1-\theta_1')(\theta_2-\theta_2') \over \vert (\thetag-\thetag') \vert^4 } \ . \end{equation}$

(17)

This equation can be inverted in order to express the projected mass density, or equivalently kappa , as function of the shear:

$\begin{equation} \kappa(\thetag)= {1 \over \pi} \int \Re[\mathcal{D}^*(\thetag-\thetag') \gammag(\thetag')] \ d^2\theta' \ + \kappa_0 \ , \end{equation}$

(18)

where 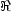denotes the real part. From Equation 14 we can express the shear as a function of the complex ellipticity. Hence, if the background ellipticity distribution is randomly distributed, then <| epsilon ^S|> = 0 and

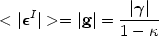$\begin{equation} <\vert \epsilong^I \vert>= \vert \boldg \vert = {\vert \gammag \vert \over 1 - \kappa} \end{equation}$

(19)

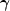(Schramm & Kayser 1995). In the most extreme case, when kappa << 1 (the linear regime discussed initially by Kaiser & Squires 1993), < | epsilon ^I| > approx | gamma |, and therefore, the projected mass density can be recovered directly from the measurement of the ellipticities of the lensed galaxies.

The first cluster mass reconstructions using the Kaiser & Squires linear inversion have been done by Smail (1993), Fahlman et al (1994). 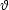Fahlman et al estimated the total mass within a circular radius using the Aperture densitometry technique (or the " zeta -statistics"), which consists of computing the difference between the mean projected mass densities within a radius r₁ and within an annulus (r₂ - r₁) (Fahlman et al 1994, Kaiser 1995) as function of the tangential shear, gamma _t = gamma ₁ cos(2 vartheta ) + gamma ₂ sin(2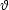) see Equation 14), averaged in the ring:

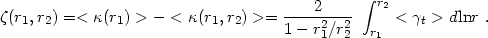$\begin{equation} \zeta(r_1,r_2)=<\kappa(r_1)>-<\kappa(r_1,r_2)>={2 \over 1-r_1^2/r_2^2} \ \int_{r_1}^{r_2} <\gamma_t> d {\rm ln}r \ . \end{equation}$

(20)

This quite robust mass estimator minimizes the contamination by foreground and cluster galaxies and permits a simple check that the signal is produced by shear, simply by changing gamma ₁ in gamma ₂ and gamma ₂ in - gamma ₁ which should cancel out the true shear signal.

The mass maps inferred from their images coincide with the light distribution from the galaxies. But, the impressive M/L found in the lensing cluster MS1224+20 by Fahlman et al (see Table 1) led to a surprisingly high value of Omega (close to 2!). This result is somewhat questionable and is probably due to the various sources of errors, possibly in the correction of PSF anisotropy (see Section 3.3). Furthermore, the two-dimensional mass reconstructions presented in the earliest papers looked noisy, probably because of boundary effects from the intrinsically non-local reconstruction, the geometry of the finite-size charge coupled device (CCD), and the reconstruction algorithm that can have terrible effects on the inversion. These problems have been discussed in several papers (Schneider & Seitz 1995, Seitz & Schneider 1995a, Schneider 1995, Seitz & Schneider 1996). 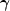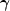In particular, Kaiser (1995), Seitz & Schneider (1996) generalized the inversion to the non-linear regime, by solving the integral equation obtained from Equation 18 by replacing gamma by (1 - kappa )g, or similarly by using the fact that both kappa and gamma depend on second derivatives of the projected gravitational potential phi (Kaiser 1995) which permits one to recover the mass density by this alternative relation:

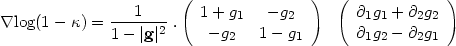$\begin{equation} \nabla {\rm log}(1-\kappa)= {1 \over 1 -\vert \boldg \vert^2} \ . \left( \begin{array}{cc} 1+g_1 & -g_2 \\ -g_2 & 1-g_1 \\ \end{array}\right) \ \ \left( \begin{array}{c} \partial_1 g_1 + \partial_2 g_2 \\ \partial_1 g_2 - \partial_2 g_1 \\ \end{array} \right) \end{equation}$

(21)

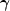Both Equations 18 and 21 express the same relation between kappa and gamma and can be used to reconstruct the projected mass density. The improvements that have been proposed and discussed in detail by Seitz & Schneider (1995a), Kaiser (1995), Schneider (1995), Bartelmann (1995c), Squires & Kaiser (1996), Seitz & Schneider (1996, 1997), Lombardi & Bertin (1998a, b) lead to reliable mass reconstructions from lensing inversion, and comparison with simulated clusters proves that it can now be considered a robust technique (see Figure 4, in particular the comparision between Figure 4a, Figures 4g and 4h). However, the recovered mass distribution is not unique because the addition of a lens plane with constant mass density will not change the distortion of the galaxies (see Equation 18). 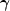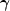Furthermore, the inversion only uses the ellipticity of the galaxies without regard to their dimension, so that changing (1 - kappa ) in lambda (1 - kappa ) and gamma in lambda gamma keeps g invariant. This so-called mass sheet degeneracy initially reported by Gorenstein et al (1988), has been pointed out by Schneider & Seitz (1995) as a fundamental limitation of the lensing inversion.

**Table 1.** Main results obtained from weak lensing analyses of lensing-clusters. The scale is the typical radial distance with respect to the cluster center. The last cluster has two values for the M/L ratio. This corresponds to two extreme redshifts assumed for the lensed population, either z = 3 or z = 1.5. For this case, the two values given for the velocity dispersion are those inferred when z = 3 or z = 1.5 are used.

Cluster	z	_obs (km s^-1)	_wl (km s^-1)	M/L (h₁₀₀)	Scale (h₁₀₀^-1 Mpc)	Tel.	Ref.

A2218	0.17	1370	-	310	0.1	HST	Smail et al (1997)
A1689	0.18	2400	1200-1500	-	0.5	CTIO	Tyson et al (1990)
			-	400	1.0	CTIO	Tyson & Fischer (1995)
A2163	0.20	1680	740-1000	300	0.5	CFHT	Squires et al (1997)
A2390	0.23	1090	1000	320	0.5	CFHT	Squires et al (1996b)
Cl1455+22	0.26	700	-	1080	0.4	WHT	Smail et al (1995)
AC118	0.31	1950	-	370	0.15	HST	Smail et al (1997)
Cl1358+62	0.33	910	780	180	0.75	HST	Hoekstra et al (1998)
MS1224+20	0.33	770	-	800	1.0	CFHT	Fahlman et al (1994)
Q0957+56	0.36	715	-	-	0.5	CFHT	Fischer et al (1997)
Cl0024+17	0.39	1250	-	150	0.15	HST	Smail et al (1997)
			1300	900	1.5	CFHT	Bonnet et al (1994)
Cl0939+47	0.41	1080	-	120	0.2	HST	Smail et al (1997)
			-	250	0.2	HST	Seitz et al (1996)
Cl0302+17	0.42	1080		80	0.2	HST	Smail et al (1997)
RXJ1347-11	0.45	-	1500	400	1.0	CTIO	Fischer & Tyson (1997)
3C295	0.46	1670	1100-1500	-	0.5	CFHT	Tyson et al (1990)
			-	330	0.2	HST	Smail et al (1997)
Cl0412-65	0.51	-	-	70	0.2	HST	Smail et al (1997)
Cl1601+43	0.54	1170	-	190	0.2	HST	Smail et al (1997)
Cl0016+16	0.55	1700	-	180	0.2	HST	Smail et al (1997)
			740	740	0.6	WHT	Smail et al (1993)
Cl0054-27	0.56	-	-	400	0.2	HST	Smail et al (1997)
MS1137+60	0.78	859¹	-	270	0.5	Keck	Clowe et al (1998)
RXJ1716+67	0.81	1522²	-	190	0.5	Keck	Clowe et al (1998)
MS1054-03	0.83	1360³	1100-2200	350-1600	0.5	UH2.2	Luppino & Kaiser (1997)

¹Gioia, private communication.
²Gioia et al (1998).
³Donahue et al (1998).

Figure 4. Examples of different algorithms for the mass reconstruction of clusters. Image A (top left) is the original simulated lensing cluster. Panel B shows an original Kaiser & Squires (1993) mass reconstruction, assuming that all background sources are circular. Panel C shows the same reconstruction as panel B, but with another smoothing method, which was proposed by Seitz & Schneider (1995a), in order to smooth the distortion distribution. Panel D shows the same result but the sources have an ellipticity distribution. Panel E shows the same reconstruction as panel D, but uses an adaptive smoothing scale. In panel F the linear and non-linear weak lensing regimes are now used in the inversion. Panel G shows the same reconstruction algorithm as F, with an additional extrapolation of the distortion field outside the field. The last panel shows the mass reconstruction with the constraint that the minimal mass density at any point is zero (from Seitz & Schneider 1995a).

The degeneracy could in principle be broken if the magnification can be measured independently, because it is not invariant under the linear transformation mentioned above, but instead it is reduced by a factor of 1 / lambda ². Broadhurst et al (1995) proposed measuring the magnification directly by using the magnification bias which changes the galaxy number-counts (see Section 3.4), whereas Bartelmann & Narayan (1995) explored their lens parallax method which compares the angular sizes of lensed galaxies with an unlensed sample. The lens-parallax method requires a sample of unlensed population having the same surface brightness distribution. However, in the case of ground-based observations, for the faintest (i.e. smallest galaxies), the convolution of the signal by the seeing disk can significantly affect the measurement of their surface brightness. Therefore, the method requires a careful handling of small-sized objects. A more promising approach is the use of wide field cameras with a typical field of view much larger than clusters of galaxies. In that case kappa should vanish at the boundaries of the field, so that the degeneracy could in principle be broken.

An attractive alternative has been suggested by Bartelmann et al (1996) who proposed a maximum likelihood reconstruction algorithm. The advantage is that this is a local approach because it fits the projected potential at each grid-point. The observables are constrained by the second-derivatives of the potential, using a least- chi ² which simultaneously computes both the magnification and the distortion, which are compared to the ellipticity and the sizes of the galaxies. Squires & Kaiser (1996), Bridle et al (1998) have investigated similar maximum-likelihood techniques with different regularizations, though they fit the projected mass density rather than the potential. It seems however more attractive to use the deflection potential rather than the projected mass distribution in order to avoid incomplete knowledge of the contribution to the projected mass density of the matter outside the observed area (Seitz et al 1998).

The comparison done by Squires & Kaiser (1996) between the direct reconstructions, like the Kaiser & Squires (1993) approach, and the inversion methods, like the maximum likelihood reconstructions, did not lead to conclusive results, though the maximum likelihood inversion looks somewhat better. It is worth pointing out that one of the advantages of the maximum likelihood inversion is that it eases the addition of some observational constraints, such as strong lensing features (Bartelmann et al 1996; Seitz et al 1998). More recently, Seitz et al (1998) proposed an improved entropy-regularized maximum-likelihood inversion in which they no longer smooth the data, but instead use the ellipticity of each individual galaxy.

Since 1990, many clusters have been investigated using the weak lensing inversion, using either ground-based or HST data that are summarized in Table 1, but the comparison of these results is not straightforward because of the different observing conditions which produced each set of data and the different mass reconstruction algorithms used by each author. Nevertheless, all these studies show that on scales of about 1 Mpc, the geometry of mass distributions, the X-ray distribution and the galaxy distribution are similar (see Figure 5), although the ratio of each component compared with the others may vary with radius. The inferred M/L ratio lies between 100h₁₀₀ to 1600h₁₀₀, with a median value of approximately 300h₁₀₀, with a trend to increase with radius. Contrary to the strong lensing cases, there is no evidence of discrepancies between the X-ray mass and the weak lensing mass. It is worth noting that the strong-lensing mass and the weak-lensing mass estimates are consistent in the region where the amplitudes of two regimes are very close. This is an indication that the description of the X-ray gas, and its coupling with the dark matter on the scales corresponding to strong-lensing studies, is oversimplified, whereas on larger scales, described by weak-lensing analysis, the detailed description of the gas has no strong impact.

Figure 5. Weak lensing analysis and mass reconstruction of A2218 (from Squires et al 1996a). The images have been obtained at CFHT in I-band. The top-left panel shows the smoothed galaxy number density and the top-right shows the smoothed light distribution. The bottom-left is the shear map. The length of each line is proportional to the amplitude of the shear. From this shear map, the mass reconstruction of the Kaiser & Squires (1993) algorithm produces the mass map on the bottom-right. The correlation between the light and the matter distribution is clear.

The large range of M/L could partly be a result of one of the issues of the mass reconstruction from weak lensing. As shown in Equation 1, the deviation angle depends on the ratios of the three angular-diameter distances, which vary with the redshift assumed for the sources. For low-z lenses, the dependence with redshift of the background galaxies is not considerable, so the calibration of the mass can be provided with a reasonable confidence level. However, distant clusters are highly sensitive to the redshift of the sources, and it becomes very difficult to scale the total mass without this information, even though the shape of the projected mass density is reconstructed correctly. The case of high-redshift clusters is more complicated. For a low-z cluster (say z < 0.4), it is not necessary to go extremely deep since the background galaxies are between z = 0.4 to 1. Thus, spectroscopic surveys can provide the redshift distribution with a good accuracy. In contrast, the background sources lensed by high-z clusters are beyond z = 1 and therefore are dominated by very faint galaxies (I > 22.5) which cannot be observed easily by spectroscopy.

The masses inferred from the strong lensing and weak lensing reconstruction put valuable constraints on the median M/L of lensing clusters. From the investigation of about 20 clusters, the median M/L is lower than 400h₁₀₀. This implies that weak lensing analyses predict Omega < 0.3 with a high significance level. Even if the uncertainties are large and if the weak lensing inversion needs to be improved, the HST data, in particular for clusters with giant arcs and many arc(let)s with known redshift, imply that the mass of clusters of galaxies cannot be reconciled with an Einstein-de Sitter (EdS) universe. The constraints on Omega are in good agreement with other observations (see the recent discussion by Krauss 1998).

Another strong statement results from the mass reconstruction obtained by Luppino & Kaiser (1997), Clowe et al (1998) or the detection of giant arcs in very distant clusters (Deltorn et al 1997): massive clusters do exist at redshift approx 1! Though the total mass and the M/L cannot be given with a high accuracy, it cannot change the conclusion, unless unknown important systematics have been neglected. Therefore, we now have the first direct observational evidences that high mass-density peaks have generated massive clusters of galaxies at redshift 1. These results are extremely promising and are corroborated by other weak lensing studies around radiosources and quasars (see Section 4.2). Indeed, because these studies question the standard Cold Dark Matter can certainly expect fantastic developments from the investigation of high-redshift clusters with weak lensing during the coming years.

The impressive and spectacular results obtained by weak-lensing have demonstrated the power of this technique. However, although the results seem reliable in the cluster center (say within 500 kpc), there are still uncertainties outward, where the shear becomes very small. A critical issue of the lensing inversion is the reliability of the mass reconstruction and how it degrades when the shear decreases. Kaiser (1995) emphasized that Equation 20 can be used as a check of the mass reconstruction since the curl of nabla log(1 - kappa ) should be zero only if the shear is recovered properly. Van Waerbeke (1999) has recently proposed an elegant way to estimate the accuracy of the mass reconstruction from the noise properties of the reconstruction. Nevertheless, the comparison of results using different algorithms and the stability and the reproducibility of each inversion have still to be done in order to demonstrate that weak lensing analysis produces reliable results. This is important for the future, when ground-based observations of very large fields will be performed. Mellier et al (1997) have compared the shear maps obtained in A1942 by using the Bonnet-Mellier and the autocorrelation function (ACF) methods (see next section). Though the two maps are similar, discrepancies are visible at the periphery, but no quantitative estimates of the similarity of both maps are given. An important step was taken by Van Waerbeke et al (in preparation) who analyzed A1942 using different shear measurements, different mass reconstruction algorithms and different data, obtained with two CCD cameras mounted at CFHT. Three sets of data have been used, all of them having a total exposure time of 4 hours and a seeing of 0.7". The results show impressive similarities even in the details of the mass reconstruction, down to a shear amplitude of 2%. This is the first work that demonstrates that results are stable and are not produced by artifacts, even at a very low shear amplitude. The main concerns are the capabilities of instruments, and the image analysis algorithms to measure very weak shear. This critical issue deserves a detailed discussion, which is the subject of the next section.