Copyright © 1996 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1996. 34:
461-510 Copyright © 1996 by Annual Reviews. All rights reserved |
3.2. Distances Based on RR Lyraes
As noted in Section 2.6, the level of the horizontal branch at the color of the instability strip, which we refer to as MV(HB) (although any bandpass can be used), has been used for ~ 40 years to set the distance to a globular cluster. This value is defined to be the mean absolute magnitude of the cluster RR Lyrae stars after a proper averaging over each star's pulsational cycle. However, because horizontal-branch stars evolve to brighter magnitudes on their way to the asymptotic giant branch, there is an evolutionary width in the brightness of the HB (see Sandage 1990a); consequently, when comparing literature data for MV(HB), care must be taken to ensure that the level of the HB is being compared for stars that have undergone the same amount of evolution.
It has long been suspected (cf Sandage 1958) that MV(HB) is a function of [Fe/H] - considering equivalent evolutionary states - in the sense that more metal-poor HB stars are more luminous. As a result, a linear relation of the form MV(HB) = c0 + c1 [Fe/H] has generally been assumed, and a concerted effort has been made to try to determine the constants c0 and c1. The first of these constants is of critical importance for determining the age of the oldest GCs, while the second has a strong influence on the inferred age-metallicity relation that describes these systems (see, e.g. Sandage & Cacciari 1990, Walker 1992). Unfortunately, even the nearest RR Lyrae is too far away for a direct trignometric parallax distance; consequently, it has been necessary to use more indirect approaches to determine their MV values. These include statistical parallaxes of field variables (e.g. Hawley et al 1986, 1996), Baade-Wesselink (B-W) analyses of field and cluster RR Lyraes (e.g. Liu & Janes 1990a, b, Storm, Carney & Latham 1994), main-sequence fits to GCs (Buonanno et al 1990, Bolte & Hogan 1995), and pulsation theory (Sandage, Katem & Sandage 1981, Sandage 1993b).
Figure 9 provides a graphical summary of the current status of this endeavor. The filled squares give the B-W results of Jones et al (1992), supplemented by an additional two stars from earlier work by Liu & Janes (1990a) that were not considered by the former. (Both investigations analyzed essentially the same sample of field RR Lyraes and both obtained very similar MV values, generally agreeing to within 0.03 mag.) The solid curve gives the linear fit to these data adopted by Storm et al (1994) specifically, MV(HB) = 1.02 + 0.16 [Fe/H]. The slope of this relation is very similar to that of the dotted line, which represents the variation that Dorman (1993) computed from his zero-age main-sequence (ZAHB) models for scaled-solar abundances. It has c0 = 0.85 and c1 = 0.19, which are exceedingly close to the coefficients that Renzini (1991) determined from the ZAHBs in Sweigart, Renzini & Tornambè (1987).
 |
Figure 9. MV(HB) vs [Fe/H] results from various sources. The closed squares represent the data for individual field RR Lyraes as obtained from the Baade-Wesselink analyses of Jones et al (1992), Liu & Janes (1990a). The solid line gives the fit to these observations that was adopted by Storm et al (1994). Also based on the B-W method, the Liu & Janes (1990b) findings for four M4 variables are indicated by open triangles and the Storm et al results for RR Lyraes in M5 and M92 are denoted by open circles and open squares, respectively. The statistical parallax determinations by Hawley et al (1995) are represented by the closed triangles with attached error bars. The cross indicates Walker's (1992a) LMC estimate. The three-pointed star depicts the mean magnitude of M15 RR Lyraes as determined by Silbermann & Smith (1995). The dotted line gives the predicted ZAHB relation, as computed by Dorman (1993). The dashed line illustrates the relation between RR Lyrae magnitudes and [Fe/H] derived by Sandage (1993b) from his analysis of the Oosterhoff-Arp period-metallicity relation. |
Why the B-W MV values are fainter, at a given [Fe/H],
than the theoretically predicted
values is hard to explain unless 1. the field RR Lyraes have a helium
abundance that is significantly lower than the Y
 0.23 assumed in the models, 2. the application of the B-W method introduces
a 0.2 mag zero-point error, or 3. the stellar interior computations are
somehow
deficient. The first option seems improbable in view of the
R-method results and the present consensus that the primordial
helium abundance was near Y
= 0.23 (see Section 2.4). Concerning
the last option, the only possibility
that occurs to us is that the reduction in the envelope helium abundance
due to diffusion has been underestimated (see
Section 2.2.1). (Smaller core
masses might also work, but there is no other reason to doubt our present
understanding of the neutrino emission processes that largely determine the
thermal structure of the core during RGB evolution.) Otherwise, any
noncanonical
process that might be going on, such as deep mixing or rapid core rotation,
would tend to make the models brighter rather than fainter. A zero-point
error could well be the most probable solution given that
Carney, Storm &
Jones (1992) themselves suspect that c0 has a
± 0.15 mag uncertainty (also see
Cohen 1992,
Fernley 1994).
This question awaits a satisfactory resolution.
0.23 assumed in the models, 2. the application of the B-W method introduces
a 0.2 mag zero-point error, or 3. the stellar interior computations are
somehow
deficient. The first option seems improbable in view of the
R-method results and the present consensus that the primordial
helium abundance was near Y
= 0.23 (see Section 2.4). Concerning
the last option, the only possibility
that occurs to us is that the reduction in the envelope helium abundance
due to diffusion has been underestimated (see
Section 2.2.1). (Smaller core
masses might also work, but there is no other reason to doubt our present
understanding of the neutrino emission processes that largely determine the
thermal structure of the core during RGB evolution.) Otherwise, any
noncanonical
process that might be going on, such as deep mixing or rapid core rotation,
would tend to make the models brighter rather than fainter. A zero-point
error could well be the most probable solution given that
Carney, Storm &
Jones (1992) themselves suspect that c0 has a
± 0.15 mag uncertainty (also see
Cohen 1992,
Fernley 1994).
This question awaits a satisfactory resolution.
Statistical parallaxes of field RR Lyrae stars also give a faint value for the HB brightness zero-point, but with a very large uncertainty. (This approach is subject to the assumption that the kinetmatic properties of the RR Lyrae population are, to first order, constant over the volume sampled.) Although the studies of Hawley et al (1986), Barnes & Hawley (1986), Strugnell, Reid & Murray (1986) treated the existing data with a sophisticated set of analysis tools, there have remained some question marks regarding systematic errors in the proper motion lists available at the time and the use of a heterogeneous mix of [Fe/H] and radial velocity data. However, the recent reanalysis of the statistical parallax solution using a homogenous set of proper motion data based on an extragalactic coordinate system and new observations of [Fe/H] and radial velocity (Hawley et al 1995) has yielded essentially the same brightness zero-point as the earlier studies. (Note the location of the closed triangles with attached error bars in Figure 9.)
Beginning with the Cohen & Gordon (1987) investigation, there have been a number of attempts to carry out B-W analyses of cluster (as opposed to field) RR Lyraes. The open symbols in Figure 9 represent the results that Liu & Janes (1990b) obtained for M4 along with those derived for M5 and M92 by Storm et al (1994). (There has been a considerable evolution in the application of the B-W method over the years with the switch from BV to near-infrared photometry, the recognition that certain phases of the light curves give inconsistent results due to well-understood violations of assumptions, and the development of improved procedures for fitting the data. Thus only the latest determinations have been included in our figure.) Whereas the M4 RR Lyraes appear to be completely consistent with the field-star relation between MV(HB) and [Fe/H], that is apparently not true of the two M92 pulsators, and possibly not of the M5 variables, although Storm et al (1994) suggest that the difference is not significant in the latter case.
Based on the two RR Lyraes studied, Storm et al (1994) derived (m - M)0 = 14.60 ± 0.26 for M92, i.e. effectively the same distance that Stetson & Harris (1988), Bolte & Hogan (1995), and we (in Section 3.1) obtained from the fitting of the nearby subdwarfs to the cluster main sequence. Storm et al expressed the concern that the two M92 variables might be highly evolved from the ZAHB, which would explain their displacement from the field-star relation, but there is additional evidence in support of the brighter luminosity scale. From CCD observations of 182 RR Lyraes in seven Large Magellanic Cloud clusters, Walker (1992) determined a mean MV of 0.44 mag at [Fe/H] = - 1.9 (the cross in Figure 9), assuming the Cepheid-based distance modulus of 18.5 (which should be accurate to within ± 0.1 mag). Curiously, Walker (1989) found the field RR Lyraes in the vicinity of the LMC cluster NGC 2257 to be 0.17 mag fainter, in the mean, than the cluster variables. Although this could simply be telling us that the cluster is closer than the average distance of the field stars, it could also be indicating a fundamental difference between the two stellar populations (a possible interpretation of the M92 results, as well). In addition, we note the determination of MV = 0.36 ± 0.12 (the three-pointed star in Figure 9) for the M15 variables from an analysis of their pulsational properties (Silbermann & Smith 1995).
Lastly, there is the
Sandage (1993b)
relation, MV(HB) = 0.94+0.30 [Fe/H] (the dashed curve
in Figure 9), which is based on his analysis of
the Oosterhoff-Arp period versus metallicity correlation:
Oosterhoff (1939,
1944)
showed that GCs separate into two groups according to the mean periods
of their respective RR Lyrae populations, while
Arp (1955)
discovered that the separation was one of cluster metal abundance. Based
on several pieces of evidence,
Sandage (1993a)
concluded that the Oosterhoff-Arp effect is well described by d
log P / d[Fe/H] = - 0.12 ± 0.02, where P is
the mean period (in days) of the ab-type RR Lyraes. Then, using
the fundamental pulsation equation, P

 =
constant,
which can be turned into an equation in which P is given as a
function of the pulsator's mass, luminosity, and effective temperature -
namely,
=
constant,
which can be turned into an equation in which P is given as a
function of the pulsator's mass, luminosity, and effective temperature -
namely,
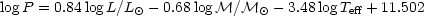 |
(van Albada &
Baker 1973)
- he inferred that the relation between MV(HB) and
[Fe/H] must be steeply sloped, with the most metal-poor variables
having rather bright magnitudes. This result made use of his deduction (in
Sandage 1993b)
that the instability strip is shifted towards cooler temperatures by
 logTeff = 0.012 for each dex decrease in [Fe/H]. Thus,
he contended that both a luminosity and a temperature shift must
be taken into account to explain the observed period data.
logTeff = 0.012 for each dex decrease in [Fe/H]. Thus,
he contended that both a luminosity and a temperature shift must
be taken into account to explain the observed period data.
It is unfortunately the case that the pulsation period depends sensitively on Teff (see above), which is always very difficult to determine reliably. Prior to the Sandage (1993a, b) papers, a concerted effort had been made (see, e.g. Sandage 1982, Gratton, Ortolani & Tornambè 1986, Lee et al 1990, Sandage 1990b, Carney et al 1992, Catelan 1992, 1994; and references therein) to understand the so-called period-shift phenomenon, which is the term given to the dependence of pulsation period on metallicity at fixed amplitude, subsequently taken to be fixed Teff. If canonical stellar models for Y = 0.23 (or so) are read at fixed Teff, they are unable to produce a significant period shift between, for instance, M3 and M15 (whose observations have been central to this issue), if the RR Lyraes are near their respective ZAHB locations and if standard reddening values are assumed. Sweigart et al (1987) carried out an exhaustive examination of the models and of the relevant input physics and were unable to come up with a satisfactory explanation for the observations, unless helium is anticorrelated with metallicity (cf Sandage 1982). However, this would be completely contrary to current ideas about how chemical enrichment proceeds, as well as being in conflict with He abundance determinations from the R-method (e.g. Buonanno et al 1985) and (probably) from fits to the observed luminosity widths of cluster HB populations (e.g. Dorman et al 1989).
Hence, to maintain the canonical framework, suggestions were put forward that either the cluster reddening values that have generally been assumed are incorrect (e.g. Caputo 1988) or the RR Lyrae stars in the most metal-deficient clusters are highly evolved and are therefore much brighter than ZAHB stars (Lee, Demarque & Zinn 1990). But both of these alternatives seem indefensible. There is no doubt about M3 being essentially free of reddening, whereas the reddening of M15 has to be very close to 0.10 for the reason that this is required in order for the intrinsic colors of the turnoff stars in this cluster (see Durrell & Harris 1993) to be the same as those observed in M92 (Stetson & Harris 1988), which has the same age (VandenBerg, Bolte & Stetson 1990) and metallicity (Sneden et al 1991). The reddening of M92 is uncontroversial at E(B - V) = 0.02 mag (see Stetson & Harris 1988). [Similar arguments have been put forward concerning M68, which belongs in the same metallicity group and which shows the same period shift relative to M3 as M15 (see Walker 1994).]
As Renzini & Fusi Pecci (1988), among others, have noted, the Lee et al (1990) explanation can hardly work in clusters that have very substantial RR Lyrae populations, such as M15. The variables should not constitute a big fraction of the total number of HB stars if the former are all in high-evolved states, where the evolutionary rates are particularly rapid. Lee (1991) has attempted to counter this argument by showing that the predicted period changes from his HB simulations agree well with those observed for the M15 RR Lyraes, though the uncertainties are large and his results are not entirely satisfactory because they fail to account for the existence of some stars whose periods are decreasing with time (see Silbermann & Smith 1995). According to the Lee et al hypothesis, all of the RR Lyrae stars should be evolving towards cooler temperatures and have periods that are increasing with time.
M68, however, poses an even greater challenge than M15, because it is much richer in RR Lyraes (see Table 2 by Carney et al 1992) and has many red HB stars (Walker 1994). There is little doubt that many of the RR Lyraes in this cluster are near the ZAHB. Furthermore, if one simply superimposes its CMD onto that for M15 such that their respective turnoffs coincide, then one finds that their HBs also match (see McClure et al 1987); hence, the M15 variables are presumably also relatively near the ZAHB. If that is the case, which is by no means certain because even the color-magnitude data are not as secure as they should be (cf Figure 6 by Dorman et al 1991), then this difficulty for period-shift considerations would remain a problem for understanding the Oosterhoff-Arp effect. Even when a metallicity-dependent temperature shift of the instability strip is taken into account, it seems that canonical HB models can be reconciled with a steeply sloped period-metallicity relation only if the variables in the most metal-deficient clusters (such as M15) are significantly more evolved than those found in M3-like clusters, which are of intermediate metallicity (see Sandage 1993b).
Simon (1992), among others, has argued against such an evolutionary scenario, and if it were shown to be untenable, then canonical HB theory could well be called into question. In this regard, one cannot help but wonder whether there might be some connection with the inability of current models to account for either the chemical abundance trends along the RGBs of especially the most metal-poor GCs (see Section 2.2.2) or the luminosity functions of these same clusters (see Section 2.5). Certainly the HB of M15, in particular, has always been very hard to fathom (cf Crocker, Rood & O'Connell 1988). The main point to be emphasized here is that, although the precise slope of the relationship between log P and [Fe/H] is uncertain at the ~ 20% level, the Oosterhoff-Arp effect is beyond dispute and it must therefore be satisfactorily explained. A steeply sloped MV(HB) versus [Fe/H] relation could well be the only way to accommodate the pulsation data.
Our understanding of the Population II distance scale
is clearly less than satisfactory. The nearby subdwarfs appear to define
a tight main-sequence locus that can be used to derive the distance to any
globular cluster with accurate photometry of its main-sequence stars and
a reliable reddening estimate. When applied to M92, this approach suggests
that MV(HB)
 0m.40 at
the metal-poor end. This distance scale is consistent with the
Galactic Cepheid scale as applied to the LMC and cluster RR Lyrae stars
there.
It is also consistent with the (fairly model-dependent) magnitudes derived
for the most metal-poor cluster RR Lyraes, with B-W results for M92
(possibly), and with the luminosities inferred from the Oosterhoff-Arp
period-metallicity
relation. Taking the subdwarf distance for M92 as being free of systematic
errors, we find an age for M92 of 15.8 ± 2 Gyr based on the
VandenBerg et al
(1996)
models. (There is then an additional possible systematic error with the
evolutionary calculations; in particular, we expect a reduction of ~
1 Gyr if unhibited helium diffusion occurs). However, the unexplained
discrepancy between this bright RR Lyrae magnitude zero-point and the
fainter one derived
via B-W and statistical parallax studies of field RR Lyrae stars leaves open
the possibility that systematic errors remain in the distance scale. If the
fainter scale turns out to be the correct one, then the age derived for M92
based on the same models mentioned above would be ~ 19 Gyr.
0m.40 at
the metal-poor end. This distance scale is consistent with the
Galactic Cepheid scale as applied to the LMC and cluster RR Lyrae stars
there.
It is also consistent with the (fairly model-dependent) magnitudes derived
for the most metal-poor cluster RR Lyraes, with B-W results for M92
(possibly), and with the luminosities inferred from the Oosterhoff-Arp
period-metallicity
relation. Taking the subdwarf distance for M92 as being free of systematic
errors, we find an age for M92 of 15.8 ± 2 Gyr based on the
VandenBerg et al
(1996)
models. (There is then an additional possible systematic error with the
evolutionary calculations; in particular, we expect a reduction of ~
1 Gyr if unhibited helium diffusion occurs). However, the unexplained
discrepancy between this bright RR Lyrae magnitude zero-point and the
fainter one derived
via B-W and statistical parallax studies of field RR Lyrae stars leaves open
the possibility that systematic errors remain in the distance scale. If the
fainter scale turns out to be the correct one, then the age derived for M92
based on the same models mentioned above would be ~ 19 Gyr.
As a final remark, we point out that the CMDs of metal-rich GCs - like 47 Tuc, which is the most thoroughly studied of such systems (Hesser et al 1987) - appear to pose few difficulties for canonical stellar evolutionary theory. For instance, Bell (1992) has obtained a superb match to the entire CMD of 47 Tuc brighter than the turnoff (including the RGB, the HB, and the asymptotic giant branch), using stellar models for the observed [Fe/H] = - 0.8 (Brown, Wallerstein & Oke 1990). His fits assumed a true distance modulus of m - M = 13.33, which is identical to that recently derived by Montegriffo et al (1995) from their extensive photometry, very similar to those estimates contained in catalogues of cluster properties (cf Webbink 1985, Djorgovski 1993), and within 0.05 mag of that adopted by Hesser et al (1987), who derived an age of 13.5 Gyr. (This age should be reduced to perhaps 12 Gyr given that the models used by Hesser interactions in the equation of state.) Our supposition that the most metal-poor globular clusters are the oldest ones is almost certainly correct.