


2.6. Nuclear Binding Energy
2.6.1. Heavy Element Abundances
We consider here the binding energy released by nuclear burning in stars. We normalize the heavy element abundances to the Solar mass fractions in hydrogen, helium, and heavy elements,
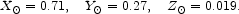 |
(85) |
The ratio Z / X = 0.027 is derived (BP2000)
as the initial solar value from
(Z / X)solar surface = 0.0230 of
Grevesse & Sauval
(2000)
and X is also the initial value of BP2000.
The metallicity in star populations is
correlated with the galaxy luminosity. An average over the Schechter
luminosity function of the
Kobulnicky & Zaritsky
(1999)
correlation of the oxygen abundance with
the B-band galaxy luminosity, taking
12 + log(O / H) = 8.83
(Grevesse & Sauval
2000)
7,
as the zero point, indicates that the mean metallicity in galaxies is
= 8.83
(Grevesse & Sauval
2000)
7,
as the zero point, indicates that the mean metallicity in galaxies is
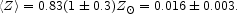 |
(86) |
Table 3 lists our estimates of the density
parameters belonging to the mass
in heavy elements in several categories of objects. The entry for main
sequence stars in the first line is the product of <Z>
with the sum of the density parameters in entries 3.3 and 3.4
in the inventory, and the second line uses entry 3.8. Since the main
elements in white dwarfs are carbon and oxygen, with thin hydrogen
and/or helium layers that typically amount to
 0.1% of the mass,
we enter
in the third line the density parameter from entry 3.5. We assign the
cool gas in entries 3.9 and 3.10 the same mean metallicity as the
stars (eq. [86]). The metallicity of the
intracluster plasma (entry 3.2) is observed to be about one third of solar
(Mushotzky &
Loewenstein 1997;
Fukazawa et al. 1998;
White 2000),
as indicated in Table 3. We suppose the
intergalactic plasma (entry 3.1) may have metallicty about 3% of
Solar. This likely is larger than the metallicity in plasma in the
voids
(Penton, Stocke &
Shull 2004),
and smaller than the metallicity
in the plasma observed as absorption line systems around galaxies
(Sembach et al. 2003;
Churchill, Vogt, &
Charlton 2003),
and perhaps
is a reasonable factor-of-three compromise. We assume that neutron
stars and stellar mass black hole form by the collapse of an
iron core, and that massive black holes grew by the accretion of
matter with about the Solar heavy element abundance. These heavy
elements are entered in Table 3, but they are now
sequestered from the inventory.
0.1% of the mass,
we enter
in the third line the density parameter from entry 3.5. We assign the
cool gas in entries 3.9 and 3.10 the same mean metallicity as the
stars (eq. [86]). The metallicity of the
intracluster plasma (entry 3.2) is observed to be about one third of solar
(Mushotzky &
Loewenstein 1997;
Fukazawa et al. 1998;
White 2000),
as indicated in Table 3. We suppose the
intergalactic plasma (entry 3.1) may have metallicty about 3% of
Solar. This likely is larger than the metallicity in plasma in the
voids
(Penton, Stocke &
Shull 2004),
and smaller than the metallicity
in the plasma observed as absorption line systems around galaxies
(Sembach et al. 2003;
Churchill, Vogt, &
Charlton 2003),
and perhaps
is a reasonable factor-of-three compromise. We assume that neutron
stars and stellar mass black hole form by the collapse of an
iron core, and that massive black holes grew by the accretion of
matter with about the Solar heavy element abundance. These heavy
elements are entered in Table 3, but they are now
sequestered from the inventory.
| Objects | Mean Metallicity | Composition | 105
 Z Z |
|
| 1 | main seq. stars | <Z> | solar | 3.2 |
| 2 | substellar objects | <Z> | solar | 0.2 |
| 3 | white dwarfs | 1 | C+O | 36 |
| 4 | cool gas | <Z> | solar | 1.3 |
| 5 | clusters |
Z /3 /3 |
solar | 1.1 |
| 6 | warm plasma |
Z /30 /30 |
solar | 2.5 |
| 7 | neutron stars a | 1 | (Fe) | 5 |
| 8 | stellar mass black holes a | 1 | (Fe) | 6.8 |
| 9 | massive black holes a | Z
 |
(solar) | 0.005 |
| a vanished | ||||
Our estimate of the total production of heavy elements, including those that have been lost in neutron stars and black holes, is
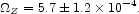 |
(87) |
The heavy elements in white dwarfs amount to about 65% of the total. The matter in this large reservoir is liberated only on the rare occasions of Type Ia supernovae.
The model for the rate of Type Ia supernovae is uncertain; we consider the widely accepted Whelan-Iben (1973) binary white dwarf picture and use a simple model for the supernova rate,
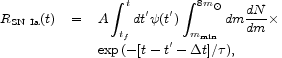 |
(88) |
where A is the normalization determined by the empirical Type Ia supernova rate at zero redshift, which is obtained from the three surveys mentioned earlier (eq. [38]),
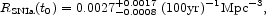 |
(89) |
and
 t(m) =
13(m /
m
t(m) =
13(m /
m )-2.5 Gyr +
)-2.5 Gyr +
 is the time for the formation of white dwarfs plus the time delay to
form the Roche-lobe contact, and we take
is the time for the formation of white dwarfs plus the time delay to
form the Roche-lobe contact, and we take
 = 0 to 1 Gyr.
The minimum mass is chosen to be mmin = max[3
m
= 0 to 1 Gyr.
The minimum mass is chosen to be mmin = max[3
m ,
{(t - t') / 13 Gyr}-0.4],
where 3m
,
{(t - t') / 13 Gyr}-0.4],
where 3m corresponds to the white dwarf mass 0.7
m
corresponds to the white dwarf mass 0.7
m according to eq. (69) so that the Chandrasekhar limit is met.
This is the model taken by
Madau et al. (1998)
(see also
Gal-Yam & Maoz
2004).
We adopt
according to eq. (69) so that the Chandrasekhar limit is met.
This is the model taken by
Madau et al. (1998)
(see also
Gal-Yam & Maoz
2004).
We adopt  = 4 Gyr to account
for a moderate increase (by a factor of 2 ± 1) of the observed SNIa
occurence to z = 0.6
(Pain et al. 2002).
8 The effective time span
for the cumulative occurrence of Type Ia supernovae
normalised to the rate at z = 0 is
= 4 Gyr to account
for a moderate increase (by a factor of 2 ± 1) of the observed SNIa
occurence to z = 0.6
(Pain et al. 2002).
8 The effective time span
for the cumulative occurrence of Type Ia supernovae
normalised to the rate at z = 0 is
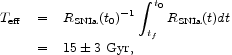 |
(90) |
for our model of star formation (eqs. [31] and [33] with
zf = 2.5 to 4). The cumulative comoving number density
of supernova in this model is 4.0 × 105 Mpc-3.
Since we estimate that the number density of white dwarfs created is
8 × 107 Mpc-3,
this would mean that about 1% of the white dwarfs have been disrupted. If
0.7m of
56Ni is produced in each supernova (e.g.,
Branch 1992),
the mass density of iron-group elements produced by type Ia supernovae is
of
56Ni is produced in each supernova (e.g.,
Branch 1992),
the mass density of iron-group elements produced by type Ia supernovae is
 Fe = 2.0
× 10-6. This is supplemented with
Fe = 2.0
× 10-6. This is supplemented with
 Fe = 3.6
× 10-6 from Type II+Ib/c supernovae, which produce
0.075m
Fe = 3.6
× 10-6 from Type II+Ib/c supernovae, which produce
0.075m of iron per event
(Arnett 1996;
Weaver, Zimmerman &
Woosley 1978).
These estimates indicate that the total density parameter in the iron
group elements is
of iron per event
(Arnett 1996;
Weaver, Zimmerman &
Woosley 1978).
These estimates indicate that the total density parameter in the iron
group elements is
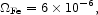 |
(91) |
of which about 60% is from Type II supernovae.
This estimate can be compared to the product of the mass in heavy elements not locked up in stellar remnants (the sum of lines 1, 2, and 4 to 6 in Table 3),
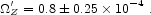 |
(92) |
with the iron group mass fraction (Grevesse & Sauval 2000),
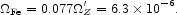 |
(93) |
The two approaches give a consistent picture for the origin of iron and the supernova rates.
The growth of the abundance of heavy elements is accompanied
by the accumulation of helium, apart from the heavy elements that enter
white dwarfs, neutron stars and stellar mass black holes. The estimate
of  Y /
Y /
 Z in equation
(19), applied to all
entries in Table 3 except 3, 7 and 8, is our
estimate of the present helium mass fraction in excess of primeval,
Z in equation
(19), applied to all
entries in Table 3 except 3, 7 and 8, is our
estimate of the present helium mass fraction in excess of primeval,
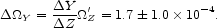 |
(94) |
This is consistent with our estimate from the products of stellar evolution (eq. [118]).
2.6.2. Nuclear Binding Energies
Our definition of the nuclear binding energies of the heavy elements differs from the usual practice in tables of nuclei. Because we are interested in the release of energy in the formation of the heavy elements, we calculate the binding energy with respect to free protons and electrons.
We write the energy released in the production of the heavy elements present in the interstellar medium, and in stars when they formed, as
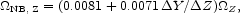 |
(95) |
where 0.0081 is the energy generation efficiency factor for the solar composition. The nuclear binding energy in substellar objects and in diffuse matter, in entries 6.2, 6.4, and 6.5 in Table 1, is computed from this equation with the heavy element masses in Table 3. For main sequence stars, we add to equation (95) the nuclear binding energy associated with the helium that has been produced in the stars, which we take to be on average 5% of the star mass, that is, half the helium a star produces while it is on the main sequence. The sum is our estimate of the nuclear binding energy in stars in entry 6.1.
Entry 6.3, for white dwarfs, is
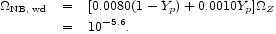 |
(96) |
The second term in parentheses accounts for the primordial helium
abundance (eq. [17]). The value of
 Z in the
first line is taken from line 3 of Table 3. This
component amounts to
about 40% of the nuclear binding energy. The large amount of nuclear
burning in the stellar giant and supergiant phases is discussed in
connection with Table 5 below.
Z in the
first line is taken from line 3 of Table 3. This
component amounts to
about 40% of the nuclear binding energy. The large amount of nuclear
burning in the stellar giant and supergiant phases is discussed in
connection with Table 5 below.
The nuclear binding energy in the matter out of which a neutron star formed was converted to gravitational binding energy by the dissociation of the heavy elements during a supernova. The nuclear binding energy released in the formation of the heavy elements that were part of the raw material for a neutron star added to the radiation background, of course, but that accounting now belongs in category 5. The total entered in the inventory for category 6 accordingly is about 15% smaller than the sum of the nuclear binding energies in all entries in Table 3. The nuclear binding energy to compare to the energy required to produce the radiation background is the full sum, including iron core progenitors for neutron stars and black holes,
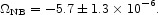 |
(97) |
We discuss the relation to the energy density in radiation in the next subsection.
7 Recent work on the solar heavy element
abundance suggests a significantly lower oxygen abundance,
12 + log(O / H) =
8.69
(Allende Prieto, Lambert
& Asplund 2001),
but if the heavy element abundances of other elements are scaled down
in a similar manner,
as indicated by the same team, our net result is not affected. In fact,
Bahcall and Pinsonneault
(2004)
give (Z / X)solar surface = 0.0176
based on the new abundance, which leaves our result unchanged.
Back.
=
8.69
(Allende Prieto, Lambert
& Asplund 2001),
but if the heavy element abundances of other elements are scaled down
in a similar manner,
as indicated by the same team, our net result is not affected. In fact,
Bahcall and Pinsonneault
(2004)
give (Z / X)solar surface = 0.0176
based on the new abundance, which leaves our result unchanged.
Back.
8 A short time scale
is in conflict with the Type Ia supernova rates in early type galaxies.
With  = 4 Gyr, the SN
fraction in early type galaxies is 0.30 at
z
= 4 Gyr, the SN
fraction in early type galaxies is 0.30 at
z  0, which is
consistent with the observed value,
0.35+0.15-0.10. Here we have identified stars
formed at z > 0.7 as an early population that is partitioned
into early-type galaxies and bulges of disk galaxies according to the
FHP fractions of bulge luminosities. The fraction drops to < 0.25 if
0, which is
consistent with the observed value,
0.35+0.15-0.10. Here we have identified stars
formed at z > 0.7 as an early population that is partitioned
into early-type galaxies and bulges of disk galaxies according to the
FHP fractions of bulge luminosities. The fraction drops to < 0.25 if
 = 3 Gyr. The observed rates
of Type Ia supernovae in morphologically separated galaxies seem to be
proportional to the r band luminosity
density; the luminosity density in E/S0 galaxies is 31% of the total
(Nakamura et al. 2003).
This would suggest a close to constant supernova rate.
Back.
= 3 Gyr. The observed rates
of Type Ia supernovae in morphologically separated galaxies seem to be
proportional to the r band luminosity
density; the luminosity density in E/S0 galaxies is 31% of the total
(Nakamura et al. 2003).
This would suggest a close to constant supernova rate.
Back.