The Cosmic Energy Inventory - M. Fukugita & P.J.E. Peebles

2.7. The Radiation Backgrounds

The cosmic energy density in electromagnetic radiation is thought to be dominated by mildly redshifted starlight, at lambda ~ 1µ, and a far infrared peak at lambda ~ 100µ that is produced by the absorption and reradiation of starlight and the light from AGNs (Hauser & Dwek 2001 and references therein). The energy densities at radio and X-ray to gamma -ray wavelengths are much smaller, but they are useful measures of high energy processes, as is the gravitational wave background. Neutrino production might be counted as part of the radiation backgrounds, but we find it convenient to enter neutrinos in a separate category.

2.7.1. The ~ 1µ Background

Observations of the optical to near infrared extragalactic background light that report positive detections are summarized in Table 4. They suggest that the surface brightness per logarithmic interval in frequency is about constant at I = 20± 5 nW m^-2 sr^-1 in the range 3500 Å to 3.5 µ. This corresponds to energy density

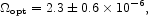(98)

in the optical to near infrared. In view of the technical difficulty of these observations, equation (98) may conservatively be taken as an upper limit. Integrated galaxy number counts give surface brightness typically one third of the entries in Table 4 (Madau & Pozzetti 2000; see also Hauser & Dwek 2001, Table 3),

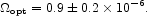(99)

This might be considered a lower limit.

**Table 4.** Radiation Background

(µ)	I (nW m^-2 sr^-1)

0.10	0.60 ^a
0.30	13 ± 8 ^b
0.37	24 ± 8 ^c
0.55	18 ± 8 ^b
0.81	24 ± 9 ^b
2.2	23 ± 9 ^d
3.5	12 ± 3 ^d

^a Henry (1999)	^b Bernstein et al. (2002)
^c Matilla (1990)	^d Wright & Reese (2000)

We have a check from the energy density computed as a time integral of the luminosity density,

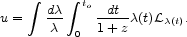(100)

The integral is from high redshift to the present world time, t_o. The integrand is the luminosity per logarithmic interval of wavelength and comoving volume, corrected by the redshift factor, 1 + z = 1 / a(t), and evaluated at the redshifted wavelength (t) = a(t) _o, where the observed wavelength is _o and the expansion parameter a(t) is normalized to unity at the present epoch. In the flat cosmological model the integral is

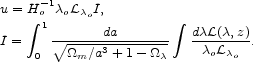(101)

We take the shape of the present cosmic spectrum lambda as a function of wavelength from Figure 13 in Blanton et al. (2003), and we normalize to the luminosity density at lambda ~ 1µ in equation (21). We approximate the evolution of the comoving luminosity density by extrapolating the Rudnick et al. (2003) power law fits to the evolution in the rest frame U, V and B bands, in the form

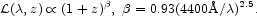(102)

We truncate the integral at z = 3, the limit of the Rudnick et al. measurements. In this model the dimensionless integral in equation (101) is I = 1.35. (If the comoving luminosity density were constant the integral would be I = 0.82.) The result is

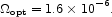(103)

The light from quasars adds about one percent of the starlight.

For the inventory we adopt

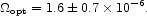(104)

The error spans the estimates based on measurements of the surface brightness of the sky (eqs. [98]), the source counts (eq. [99]) and the luminosity density (eq. [103]).

2.7.2. The Far Infrared Background

The COBE DIRBE (Hauser et al. 1998) and FIRAS (Fixsen et al. 1998) experiments detect the extragalactic radiation background at lambda gtapprox 100µ. The integral for lambda > 125µ is u = 14 nW m^-2 sr^-1 (Fixsen et al. 1998). Extending the integration to 100µ might reasonably be expected to add 2 nW m^-2 sr^-1 to this value. The density parameter for the sum is

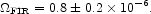(105)

This is entry 7.2 in the inventory. It seems to be a believable lower bound on the energy density in the far infrared. The radiation measurements allow room for a comparable amount of energy at 30 ltapprox lambda 100 µ (Finkbeiner, Davis & Schlegel 2000; see also Hauser & Dwek 2001). However, this amount of energy shortward of 100µ wavelength would distort the TeV gamma -ray spectrum from the extragalactic source Mrk501 (Quinn et al. 1996; Aharonian et al. 1999), by the absorption due to e⁺e^- pair production (Kneiske, Mannheim & Hartmann 2002; Konopelko et al. 2003). Thus it appears that equation (105) is close to the total in the far infrared.

2.7.3. A Check: Nuclear Burning

We may compare the estimate of the present energy density in the optical through the far infrared against what would be expected from the energy stored in the heavy elements (eq. [97]), and what would be expected from the picture for stellar evolution. We comment on the former here and the latter in Section 2.8.1.

The sum of equations (104) and (105) (entries 7.2 and 7.3), corrected for the redshift energy loss factor in equation (35), is an estimate of the nuclear energy required to produce the observed radiation,

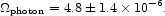(106)

This number may be compared to the nuclear binding energy released by nucleosynthesis. The estimate in equation (97), reduced by 7% to take account of the energy carried away by neutrinos, is

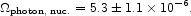(107)

The difference, 10%, is well within our uncertainties. It might be relevant to note that the difference between equations (106) and (107) would be increased if we adopted the estimate of the optical background from source counts.

2.7.4. The X-ray - -Ray Background

Entry 7.4 in Table 1 is the integral of the radiation background spectrum compiled by Gruber et al. (1999) over the energy range 3 keV to 100 GeV. The largest contribution to the integral is at photon energy ~ 30 keV, but the convergence at high energy is slow because the energy per logarithmic interval of frequency varies about as Omega ~ ^-0.1.

2.7.5. The Radio Background

Longair (1995), following Bridle's (1967) study, concludes that the brightness temperature of the isotropic radio background at 178 MHz, after correction for the thermal component, is T = 27± 7 K. This corresponds to

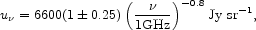(108)

assuming the canonical power law spectrum (see also Peacock 1995). Longair also argues that this radiation is dominated by galaxies.

Equation (108) may be compared to the sum of the radio source counts in the 9CR radio survey at 15 GHz, in the observed range of flux densities, 0.01 to 1 Jy (Waldram et al. 2003). This sum gives u = 5900 Jy sr^-1 when scaled to 1 GHz with the power index of 0.8. The radio source counts at 8.4 GHz by Fomalont et al. (2002), summed over 10 µJy to 1 Jy, give u = 4700 Jy sr^-1 at 1 GHz. A comparable result is obtained from the count at 40 GHZ (as summarized in Figure 13 of Bennett et al. 2003b). Haarsma & Partridge (1998) argue that the integral over the counts likely converges at S ~ 1 µJy. We conclude that the measurements are reasonably concordant with equation (108), within ~ 0.2 dex.

The integral of equation (108) slowly diverges at short wavelengths. We adopt, as an operational definition, a cutoff at lambda = 1mm ( = 300 GHz), and we count the contribution at shorter wavelengths as part of the FIR background in our inventory. There is a natural cutoff at long wavelength, at ~ 3 MHz (Simon 1978). Integrating eq. (108) over this wavelength range, we obtain

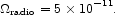(109)

To understand the relation to other energy entries, we may attempt an alternative estimate by directly summing the contributions of known radio galaxies. The luminosity function of radio galaxies at zero redshift is now reasonably well known by virtue of the correlation of a large NRAO VLA Sky Survey at 1.4 GHz (NVSS; Condon et al. 1998) with galaxies in optical catalogues (Condon, Cotton & Broderick 2002 [UGC vs. NVSS]; Machalski & Godlowski 2000 [LCRS vs. NVSS]; Sadler et al. 2002 [2dF vs. NVSS]). The luminosity function is written as the sum of two components, weak radio emitters that represent normal galaxies with star forming activity, and strong emitters that mostly consist of subsets of giant elliptical galaxies and AGNs. The former activity is ascribed to electron acceleration in Type II (and Ib/c) supernova remnants. At close to zero redshift the integral over the luminosity function gives luminosity densities

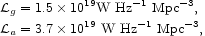(110)

at 1.4 GHz (Condon et al. 2002). The second component, AGNs, is dominated by the most luminous sources, and so is subject to sampling fluctuations. Haarsma et al. (2000) show that the evolution of the first component in equation (110) is fast to z ~ 1. The evolution they derive is consistent with the model for the evolution of the star formation rate in equation (31). Condon (1992) gives the relation between the radio emissivity and the star formation rate. After adjustment for the overall constraint from the star formation rate density derived from the local H alpha luminosity density, as discussed in Section 2.3.2, and our reference IMF, the relation reads

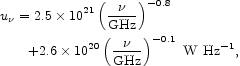(111)

per 1 m yr^-1 of star formation. The first component represents synchrotron radiation, primarily from supernovae, and the second represents bremsstrahlung from HII regions. The bremsstrahlung contribution becomes more important above 25 GHz. The integral over the star formation history to z_f = 3 (with the redshift energy loss) and the frequency range = 3 MHz to 300 GHz gives Omega _radio = 3.3 × 10^-11, where the contributions from synchrotron radiation and bremsstrahlung are in the proportion 0.4:0.6 in the frequency range that concerns us.

The evolution of the strong radio sources appears not to be very fast. The luminosity functions of Sadler et al. (2002) and Machalski & Godlowski (2000) up to z ~ 0.2 suggest a slow evolution compared with that of the weak emitter component, at least at low redshifts. We take the evolution factor derived from high redshift strong radio galaxies by Willott et al. (2001), (1 + z)^2.6 E(z) with E(z) = [ Omega _m(1 + z)³ + Omega ]^1/2, and we assume the canonical synchrotron spectrum. The integral over time and frequency yields Omega _radio = 2.0 × 10^-11. The sum of the two components is

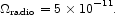(112)

The consistency with equation (109) suggests that this simple model for the radio sources is a useful approximation.

2.7.6. Gravitational Radiation

The best-understood source of gravitational radiation is close binary stars. The integrated luminosity of these sources in the Milky Way galaxy is quite uncertain, however, because of the poor constraints on the distribution of close binary systems as a function of periodicity and constituent masses. Candidates for important sources of gravitational radiation include W Ursae Majoris binary stars, at frequencies ~ 10^-4Hz (Mironowskii 1966); binaries of two main-sequence stars, which may be comparable sources of energy at lower frequencies (Hils, Bender & Webbink 1990); and close white dwarf binaries, at frequencies in the range 10^-4 -10^-2 Hz (Evans Iben & Smarr 1987). Following Hils et al. (1990), we take the typical luminosities per Milky Way galaxy to be

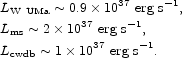(113)

The product of the sum of these quantities with the effective number density of Milky Way galaxies (eq. [54]) is our estimate of the present luminosity density. Our correction for evolution assumes the rate of formation of close binaries is proportional to the star formation rate, and that the lifetimes of these binaries are shorter than the Hubble time. Then the product of the present luminosity density with the effective time span Delta t_eff defined in equation (36) and with the redshift factor gives Omega _GW ~ 10^-12.1. Hils et al. consider that the energy in gravitational radiation from neutron star binaries is subdominant.

An entry in the inventory for possible sources of low frequency gravitational radiation in the early universe seems premature. For completeness we quote the upper limit on the gravitational wave energy density at very low frequencies obtained from pulsar timing measurements, Omega _g < 4 × 10^-9 (Lommen & Backer 2001; Kaspi, Taylor & Ryba 1994).