3.2. TRGB distance

The use of Tip of the Red Giant Branch (TRGB) as a standard candle is now a widely used technique to estimate the distance to galaxies of any morphological type (see Madore & Freedman, 1998; Lee, Freedman & Madore, 1993; Walker, 2003; Madore & Freedman, 1995, for a detailed description of the method, recent reviews and applications). The underlying physics is well understood (Salaris, Cassisi & Weiss, 2002; Madore & Freedman, 1998) and the observational procedure is operationally well defined (Madore & Freedman, 1995). The key observable is the sharp cut-off occurring at the bright end of the RGB Luminosity Function (LF) that can be easily detected with the application of an edge-detector filter (Sobel filter, Sakai, Madore & Freedman, 1996; Madore & Freedman, 1995) or by other (generally parametric) techniques (see, for example McConnachie et al., 2004; Méndez et al., 2002). The necessary condition for a safe application of the technique is that the observed RGB Luminosity Function should be well populated, with more than ~ 100 stars within 1 mag from the TRGB (Bellazzini et al., 2002; Madore & Freedman, 1995).

The F2 sample is not sufficiently populated for a safe application of the method while the F1 sample clearly fulfils the above criterion (there are more than 2500 RGB stars within 1 mag from the TRGB), hence we limit the TRGB research to F1. As a first step, to limit the range of metallicity of the stars involved in the TRGB detection, we select RGB stars by color following the approach adopted by McConnachie et al. (2004). The adopted selection includes the main bulk of the RGB population and it is shown in the lower left panel of Fig. 4. The logarithmic LF is presented as an ordinary histogram and as a generalized histogram (e.g. the histogram convolved with a Gaussian with standard deviation equal to the photometric error at the given magnitude, see Laird et al., 1988; Bellazzini et al., 2002, for definitions and references) in the upper left and upper right panels of Fig. 4, respectively. The sharp cut-off is an obvious feature of both representations of the LF and is easily detected by the Sobel filter (Fig. 4, lower right panel). As usual, the peak of the filter response is taken as the best estimate of the TRGB location and the Half Width at Half Maximum of the same peak is taken as the associated uncertainty, I^TRGB = 20.72 ± 0.08. If we consider the most recent estimates in the literature, our value is ~ 2.2 larger than that found by McConnachie et al. (2004, I^TRGB = 20.54 ± 0.01; but these authors provide only a formal error on their estimate), and ~ 1 - 2 lower than the estimates by Kim et al. (2002, I^TRGB = 20.82 - 20.92 ± 0.05 depending on the considered field), e.g. it is bracketed by the two quoted results. On the other hand our estimate is in excellent agreement with that obtained by T04 (I^TRGB = 20.75 ± 0.02).

Figure 4. Detection of the TRGB. The CMD in the lower left panel shows the adopted selection, e.g. the stars enclosed by the two diagonal lines. The arrow marks the position of the TRGB. The upper panels display the logarithmic LF of the upper RGB as an ordinary histogram (left) and as a generalized histogram (right). The thick lines marks the position of the TRGB, the thin lines enclose the associate uncertainty range. Lower panel: Response of the Sobel's filter to the observed LF.

We adopt E(B - V) = 0.04, according to the reddening maps by Schlegel et al. (1998) and Burstein & Heiles (1984) and A_I = 1.76E(B - V), according to Dean, Warren & Cousins (1978). We note however that most of the other available estimates of the foreground reddening cluster around E(B - V) = 0.08 (see Van den Bergh, 1991, and references therein). To account for this, we report also the results we obtain adopting E(B - V) = 0.08 (see Table 2, below). Note that the effects of this different assumption are small either on the final distance modulus (e.g. 0.05 mag) or the average metallicity ( 0.15 dex; see Tab. 2). According to the detailed dust maps of M 33 by Hippelein et al. (2003) the effect of the intrinsic extinction should be negligible in the fields considered here.

In Bellazzini, Ferraro & Pancino (2001) we have provided a robust zero-point to the calibrating relation providing the absolute I magnitude of the tip (M_I^TRGB) as a function of metallicity ([Fe / H], in the Zinn & West (1984) scale, hereafter ZW), based on the geometric distance to the cluster Centauri obtained by Thompson et al. (2001) using the double-lined detached eclipsing binary OGLE-17. This calibration is fully independent of the usual (Cepheid based and/or RR Lyrae based) distance scales. In Bellazzini et al. (2004) we have extended the calibration to Near Infrared passbands and we refined our I calibration providing also the relation for M_I^TRGB as a function of the global metallicity ([M/H], see Salaris, Chieffi & Straniero (1993) and Ferraro et al. (1999) for definitions and discussion) that we adopt in the present analysis.

Since the distance modulus derived from I^TRGB is weakly dependent on metallicity, and our metallicity estimates (obtained by comparison with template RGB ridge lines, see below) depend on the assumed distance modulus, we adopted an iterative method to find simultaneously the two quantities searched for. First we derived a preliminary distance modulus adopting M_I^TRGB = - 4.04, then we derived a median metallicity of the considered population as described in Sect. 3.3 below, and we obtained a refined estimate of the modulus using the obtained median metallicity ([M / H] = - 0.75, see below) as an input for the calibrating relation by Bellazzini et al. (2004):

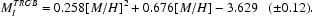(1)

The process converged to stable values of the distance modulus and of the median metallicity in 2-3 iterations, independently of the assumed reddening and/or the considered metallicity scale. Our final estimate (for E(B - V) = 0.04 and [M / H]_med = - 0.75) is (m - M)₀ = 24.64 ± 0.15, where all the sources of uncertainty have been taken into account. The corresponding distance estimate is D = 847 ± 60 Kpc.