


B.10.1. An Analytic Model for Einstein Rings
Most of the lensed extended sources we see are dominated by an Einstein
ring - this occurs when the size of the source is comparable to the size
of the astroid caustic associated with producing four-image lenses.
When the Einstein ring is fairly thin, there
is a simple analytic model for the formation of Einstein rings
(Kochanek, Keeton & McLeod
[2001]).
The important point to understand is that the ring is a pattern rather
than a simple
combination of multiple images. Mathematically, what we identify as the
ring is the peak of the surface brightness as a function of angle around
the lens galaxy. We can identify the peak by finding the maximum
intensity  (
( )
along radial spokes in the image plane,
)
along radial spokes in the image plane,
 (
( ) =
) =
 0
+
0
+  (cos
(cos ,
sin
,
sin ). At
a given azimuth
). At
a given azimuth  we find the extremum of the surface brightness of the image
fD(
we find the extremum of the surface brightness of the image
fD( ) along each spoke, and these lie at the solutions of
) along each spoke, and these lie at the solutions of
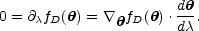 |
(B.134) |
The next step is to translate the criterion for the ring location onto
the source plane. In real images, the observed image
fD( ) is related to the actual surface density
fI(
) is related to the actual surface density
fI( ) by a convolution with the beam (PSF),
fD(
) by a convolution with the beam (PSF),
fD( ) = B*
fI(
) = B*
fI( ), but for the moment we will
assume we are dealing with a true surface brightness map. Under this
assumption fD(
), but for the moment we will
assume we are dealing with a true surface brightness map. Under this
assumption fD( ) =
fI(
) =
fI( ) =
fS(
) =
fS( ) because of surface
brightness conservation. When we change variables, the criterion for the
peak brightness becomes
) because of surface
brightness conservation. When we change variables, the criterion for the
peak brightness becomes
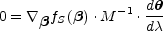 |
(B.135) |
where the inverse magnification tensor M-1 =
d /
d
/
d is
introduced by the variable transformation. Geometrically we must find
the point where the tangent vector of the curve,
M-1 .
d
is
introduced by the variable transformation. Geometrically we must find
the point where the tangent vector of the curve,
M-1 .
d /
d
/
d is perpendicular to the local gradient of the surface brightness
is perpendicular to the local gradient of the surface brightness

 fS(
fS( ). These steps are illustrated in
Fig. B.70.
). These steps are illustrated in
Fig. B.70.
This result is true in general but not very useful. We next assume that the
source has ellipsoidal surface brightness contours,
fS(m2), with m2 =

 . S .
. S .

 where
where 
 =
=  -
-  0 is the distance from the center of the source,
0 is the distance from the center of the source,
 0,
and the matrix S is defined by the axis ratio
qs = 1 -
0,
and the matrix S is defined by the axis ratio
qs = 1 -
 s
s
 1 and position angle
1 and position angle
 s of the
source. We must assume that the surface brightness declines
monotonically, dfs(m2) /
dm2 < 0, but require no
additional assumptions about the actual profile. With these assumptions
the Einstein ring curve is simply the solution of
s of the
source. We must assume that the surface brightness declines
monotonically, dfs(m2) /
dm2 < 0, but require no
additional assumptions about the actual profile. With these assumptions
the Einstein ring curve is simply the solution of
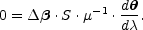 |
(B.136) |
The ring curve traces out a four (two) lobed cloverleaf pattern when
projected on the source plane if there are four (two) images of the
center of the source
(see Fig. B.70). These lobes touch the
tangential caustic at their maximum ellipsoidal distance from the source
center, and these cyclic variations
in the ellipsoidal radius produce the brightness variations seen around the
ring. The surface brightness along the ring is defined by
fI( (
( ),
),
 )
for a spoke at azimuth
)
for a spoke at azimuth
 and distance
and distance
 (
( ) found by solving
Eqn. B.135. The extrema in the surface brightness around the ring are
located at the points where
) found by solving
Eqn. B.135. The extrema in the surface brightness around the ring are
located at the points where

 fI(
fI( (
( ),
),
 ) = 0, which
occurs only at extrema
of the surface brightness of the source (the center of the source,
) = 0, which
occurs only at extrema
of the surface brightness of the source (the center of the source,

 = 0 in the ellipsoidal model), or when the
ring crosses a critical line of the lens and the magnification tensor is
singular (| M|-1 = µ-1 = 0) for the
minima. These are general results that
do not depend on the assumption of ellipsoidal symmetry.
= 0 in the ellipsoidal model), or when the
ring crosses a critical line of the lens and the magnification tensor is
singular (| M|-1 = µ-1 = 0) for the
minima. These are general results that
do not depend on the assumption of ellipsoidal symmetry.
For an SIE lens in an external shear field we can derive some simple
properties of Einstein rings to lowest order in the various axis ratios.
Let the SIE have critical radius b, axis ratio
ql = 1 -
 1 and put
its major axis along
1 and put
its major axis along
 1. Let the
external shear have amplitude
1. Let the
external shear have amplitude
 and
orientation
and
orientation 
 . We let
the source be an ellipsoid with axis ratio qs = 1 -
. We let
the source be an ellipsoid with axis ratio qs = 1 -
 s
and a major axis angle
s
and a major axis angle
 s located at
position (
s located at
position ( cos
cos 0,
0,
 sin
sin 0)
from the lens center. The tangential critical line of the lens lies at
radius
0)
from the lens center. The tangential critical line of the lens lies at
radius
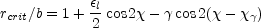 |
(B.137) |
while the Einstein ring lies at
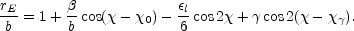 |
(B.138) |
At this order, the Einstein ring is centered on the source position
rather than the lens position. The orientation of the ring is generally
perpendicular to that of the critical curve, although it need not be
exactly so when the SIE and the shear are misaligned due to the
differing coefficients of the shear and ellipticity terms in the two
expressions. These results lead to a false impression that the results
do not depend on the shape of the source. In making the expansion we
assumed that all the terms were of the same order
( / b ~
/ b ~
 ~
~
 1 ~
1 ~
 s),
but we are really doing an expansion in the ellipticity of the potential
of the lens
e
s),
but we are really doing an expansion in the ellipticity of the potential
of the lens
e ~
el / 3 rather than the ellipticity of the density
distribution
of the lens, so second order terms in the shape of the source are as
important as first order terms in the ellipticity of the potential. For
example in a circular lens with no shear
(
~
el / 3 rather than the ellipticity of the density
distribution
of the lens, so second order terms in the shape of the source are as
important as first order terms in the ellipticity of the potential. For
example in a circular lens with no shear
( 1 = 0,
1 = 0,
 = 0) the
ring is located at
= 0) the
ring is located at
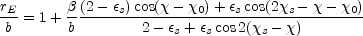 |
(B.139) |
which has only odd terms in its multipole expansion and converges slowly for flattened sources. In general, the ring shape is a weak function of the source shape only if the potential is nearly round and the source is almost centered on the lens. The structure of the lens potential dominates the even multipoles of the ring shape, while the structure of the source dominates the odd multipoles.
In fact, the shape of the ring can be used to simply "read off" the
amplitudes of the higher order multipoles of the lens potential. This is
nicely illustrated by an isothermal potential with arbitrary angular
structure,  =
rbF(
=
rbF( ) with
<F(
) with
<F( )>
= 1 (see Zhao & Pronk
[2001],
Witt et al.
[2000],
Kochanek et al.
[2001],
Evans & Witt
[2001])
in the absence of any shear. The tangential critical line of the lens is
)>
= 1 (see Zhao & Pronk
[2001],
Witt et al.
[2000],
Kochanek et al.
[2001],
Evans & Witt
[2001])
in the absence of any shear. The tangential critical line of the lens is
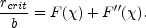 |
(B.140) |
If 
 and
and
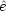
 are
radial and tangential unit vectors relative to the lens center and
are
radial and tangential unit vectors relative to the lens center and
 0 is the distance of the source from
the lens center, then the Einstein ring curve is
0 is the distance of the source from
the lens center, then the Einstein ring curve is
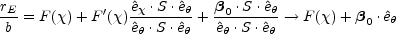 |
(B.141) |
with the limit showing the result for a circular source.
Thus, by analyzing
the multipole structure of the ring curve one can deduce the multipole
structure of the potential. While this has not been done
non-parametrically, the ability of standard ellipsoidal models to
reproduce ring curves strongly suggests that higher order multipoles
cannot be significantly different from the ellipsoidal
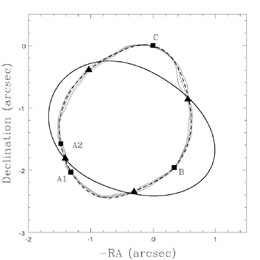
scalings. Fig. B.71 shows two examples of fits
to the ring curves
in PG1115+080 and B1938+666 using SIE plus external shear lens models. The
major systematic problem with fitting the real data are that bright
quasar images
must frequently be subtracted from the image before the ring curve can be
extracted, and this can lead to artifacts like the wiggle in the curve
between the bright A1 / A2 images of
PG1115+080. Other than that, the
accuracy with which the ellipsoidal (plus shear) models reproduce the curves
is consistent with the uncertainties. In both cases the host galaxy is
relatively flat (qs = 0.58 ± 0.02 for PG1115+080 and 0.62 ± 0.14 for
B1938+666). The flatness of the host explains the
"boxiness" of the
PG1115+080 ring, while the B1938+666 host galaxy shape is poorly constrained
because the center of the host is very close to the center of the lens
galaxy so the shape of the ring is insensitive to the shape of the source.
Unless the source is significantly offset from the center of the lens,
as we might see for the host galaxy of an asymmetric two-image lens, it
does not constrain the radial density profile of the lens very well -
after considerable algebraic effort you can show that the dependence on the
radial structure scales as
|
 |4. It can, however, help
considerably in this circumstance because it eliminates the angular degrees
of freedom in the potential that make it impossible for two-image lenses
to constrain the radial density profile at all.
|4. It can, however, help
considerably in this circumstance because it eliminates the angular degrees
of freedom in the potential that make it impossible for two-image lenses
to constrain the radial density profile at all.
 |
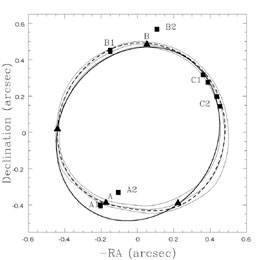 |
Figure B.71. The Einstein ring curves in PG1115+080 (top) and B1938+666 (bottom). The black squares mark the lensed quasar or compact radio sources. The light black lines show the ring curve and its uncertainties. The black triangles show the intensity minima along the ring curve (but not their uncertainties). The best fit model ring curve is shown by the dashed curve, and the heavy solid curve shows the critical line of the best fit model. The model was not constrained to fit the critical line crossings. |