B.6.4. Optical Depth

The optical depth associated with a cross section is the fraction of the sky in which you can place a source and see the effect. This simply requires adding up the contributions from all the lens galaxies between the observer and the redshift of the source. For the SIS lens we simply need to know the comoving density of lenses per unit dark matter velocity dispersion dn / d (which may be a function of redshift)

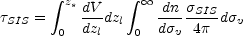(B.106)

where dV / dz_l is the comoving volume element per unit redshift (e.g. Turner, Ostriker & Gott [1984]). For a flat cosmology, which we adopt from here on, the comoving volume element is simply dV = 4 D_d² dD_d where D_d is the comoving distance to the lens redshift (Eqn. B.2). As with most lens calculations, this means that the expression simplifies if expressed in terms of the comoving angular diameter distances,

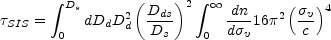(B.107)

(Gott, Park & Lee [1989], Fukugita, Futamase & Kasai [1990]). If the comoving density of the lenses does not depend on redshift, the integrals separate to give

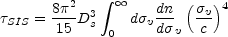(B.108)

(Fukugita & Turner [1991]). If we now assume that the galaxies can be described by the combination of Schechter luminosity functions and kinematic relations described in Section B.6.2, then we can do the remaining integral to find that

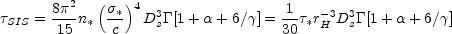(B.109)

where [x] is a Gamma function, r_H = c / H₀ is the Hubble radius and the optical depth scale is

(B.110)

Thus, lens statistics are essentially a volume test of the cosmology (the D_s³), predicated on knowing the comoving density of the lenses (n_*) and their average mass (_*). The result does not depend on the Hubble constant - all determinations of n_* scale with the Hubble constant such that n_* D_s³ is independent of H₀.

Two other distributions, those in image separation and in lens redshift at fixed image separation, are easily calculated for the SIS model and useful if numerical for any other lens. The SIS image separation is = 8(_v / c)² D_ds / D_s, so

(B.111)

where = ( / _*)^_FJ/2 and

(B.112)

is the maximum separation produced by an L_* galaxy. The mean image separation,

(B.113)

depends only on the properties of the lens galaxy and not on cosmology. If the cosmological model is not flat, a very weak dependence on cosmology is introduced (Kochanek [1993c]). For a known separation , the probability distribution for the lens redshift becomes

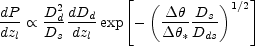(B.114)

(we present the result only for Schechter function = - 1 and Faber-Jackson _FJ = 4). The location of the exponential cut off introduced by the luminosity function has a strong cosmological dependence, so the presence or absence of lens galaxies at higher redshifts dominates the cosmological limits. The structure of this function is quite different from the total optical depth, which in a flat cosmology is a slowly varying function with a mean lens distance equal to one-half the distance to the source. The mean redshift changes with cosmology because of the changes in the distance-redshift relations, but the effect is not as dramatic as the redshift distributions for lenses of known separation.

We end this section by discussing the Keeton ([2002]) "heresy". Keeton ([2002]) pointed out that if you used a luminosity function derived at intermediate redshift rather than locally, then the cosmological sensitivity of the optical depth effectively vanishes when the median redshift of the lenses matches the median redshift of the galaxies used to derive the luminosity function. The following simple thought experiment shows that this is true at one level. Suppose there was only one kind of galaxy and we make a redshift survey and count all the galaxies in a thin shell at redshift z, finding N galaxies between z and z + z. The implied comoving density of the galaxies, n = N / ( z dV / dz), depends on the cosmological model with the same volume factor appearing in the optical depth calculation (Eqn. B.106). To the extent that the redshift ranges and weightings of the galaxy survey and a lens survey are similar, the cosmological sensitivity of the optical depth vanishes because the volume factor cancels and the optical depth depends only on the number of observed galaxies N. This does not occur when we use a local luminosity function because changes in cosmology have no effect on the local volume element. The problem with the Keeton ([2002]) argument is that it basically says that if we could use galaxy number counts to determine the cosmological model then we would not need lensing to do so because the two are redundant. To continue our thought experiment, we also have local estimates n_local for the density of galaxies, and as we vary the cosmology we would find that n and n_local agree only for a limited range of cosmological models and this would restore the cosmological sensitivity. The problem is that the comparison of near and distant measurements of the numbers of galaxies is tricky because it depends on correctly matching the galaxies in the presence of galaxy evolution and selection effects - in essence, you cannot use this argument to eliminate the cosmological sensitivity of lens surveys unless you think you understand galaxy evolution so well that you can use galaxy number counts to determine the cosmological model, a program of research that has basically been abandoned.