C. Synchrotron

Synchrotron radiation play, most likely, an important role in both the GRB and its afterglow. An important feature of synchrotron emission is its polarization (see Section VF). Observations of polarization in GRB afterglows and in one case in the prompt emission support the idea that synchrotron emission is indeed taking place there (note however that IC also produces polarized emission). I review here the basic features of synchrotron emission focusing on aspects relevant to GRBs. I refer the reader to Rybicki and Lightman [361] for a more detailed discussion.

1. Frequency and Power

The typical energy of synchrotron photons as well as the synchrotron cooling time depend on the Lorentz factor _e of the relativistic electron under consideration and on the strength of the magnetic field . If the emitting material moves with a Lorentz factor the photons are blue shifted. The characteristic photon energy in the observer frame is given by:

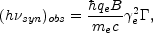(16)

where q_e is the electron's charge.

The power emitted, in the local frame, by a single electron due to synchrotron radiation is:

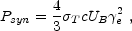(17)

where U_B B² / 8 _B e is the magnetic energy density and _T is the Thompson cross section. The cooling time of the electron in the fluid frame is then _e m_e c² / P. The observed cooling time t_syn is shorter by a factor of :

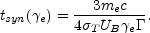(18)

Substituting the value of _e from equation 16 into the cooling rate Eq. 18 one obtains the cooling time scale as a function of the observed photon energy:

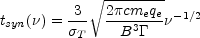(19)

Since _e does not appear explicitly in this equation t_syn at a given observed frequency is independent of the electrons' energy distribution within the shock. This is provided, of course, that there are electrons with the required _e so that there will be emission in the frequency considered. As long as there is such an electron the cooling time is "universal". This equation shows a characteristic scaling of t_syn() ^-1/2. This is not very different from the observed relation T ^-0.4 [93]. However, it is unlikely that cooling and not a physical process determines the temporal profile.

The cooling time calculated above sets a lower limit to the variability time scale of a GRB since the burst cannot possibly contain spikes that are shorter than its cooling time. Observations of GRBs typically show asymmetric spikes in the intensity variation, where a peak generally has a fast rise and a slower decay. A plausible explanation of this observation is that the shock heating of the electrons happens rapidly (though episodically), and that the rise time of a spike is related to the heating time. The decay time is then set by the cooling, so that the widths of spikes directly measure the cooling time. However, it seems that there are problems with this simple explanation. First when plugging reasonable parameters one finds that the decay time as implied by this equation is too short. Second, if the cooling time is long the shocked region would suffer adiabatic losses and this would reduce the efficiency of the process. Thus it is unlikely that the pulse shapes can be explained by Synchrotron physics alone.

2. The Optically thin Synchrotron Spectrum

The instantaneous synchrotron spectrum of a single relativistic electron with an initial energy _e m_e c² is approximately a power law with F ^1/3 up to _syn(_e) and an exponential decay above it. The peak power occurs at _syn(_e), where it has the approximate value

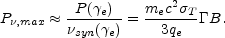(20)

Note that P_{, max} does not depend on _e, whereas the position of the peak does.

If the electron is energetic it will cool rapidly until it will reach _e,c, the Lorentz factor of an electron that cools on a hydrodynamic time scale. For a rapidly cooling electron we have to consider the time integrated spectrum. For an initial Lorentz factor _e: F ^-1/2 for _syn(_e,c) < < _syn(_e).

To calculate the overall spectrum due to the electrons one needs to integrate over the electron's Lorentz factor distribution. I consider first, following [375], a power-law distribution a power index p and a minimal Lorentz factor _e,min. This is, of course, the simplest distribution and as discussed in Section VB this is the expected distribution of shock accelerated particles:

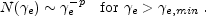(21)

The condition p > 2 is required so that the energy does not diverge at large _e (Bhattacharya [28], Dai and Cheng [64] consider also distributions with 2 > p > 1 with a maximal energy cutoff, see below). The minimum Lorentz factor, _e,min, of the distribution is related to the electron's energy density e_e and the electron's number density n_e as:

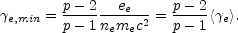(22)

The minimal Lorentz factor plays an important role as it characterizes the `typical' electron's Lorentz factor and the corresponding `typical' synchrotron frequency, _{m syn}(_e,min). Interestingly the upper energy cutoff (which essentially exists somewhere) does not play a critical role in the spectrum for p > 2. Of course it will lead to a high frequency cutoff of the spectrum around _syn that corresponds to this energy. However, quite generally, this happens at the high energy tail far from where the peak flux or the peak energy are emitted.

A simple modification of the above idea arises if only a fraction, _e, of the electrons is accelerated to high energies and the rest of the electrons remain cold [47, 154]. If a small fraction of electrons shares the energy e_e then the typical Lorentz factor would be _e^-1 _e,min, where _e,min is calculated from Eq. 22 above. All the corresponding places where _e,min is used should be modified according to this factor. At the same time fewer electrons will be radiating. This will introduce a factor _e that should multiply the total emitted flux. In the following discussion I will not add this factors into the analysis. Similarly in situations when multiple pair are formed [124] the electron's energy is shared by a larger number of electron. In this case _e is larger than unity and similar modifications of the spectrum applies.

The lowest part of the spectrum (strictly speaking the lowest part of the optically thin spectrum, as at very low frequencies self absorption sets in, see Section VC3 below) is always the sum of the contributions of the tails of all the electron's emission: F ^1/3. This is typical to synchrotron [55, 184, 258] and is independent of the exact shape of the electron's distribution. Tavani [401, 402], for example obtain such a low energy spectrum both for a Gaussian or for a Gaussian and a high energy power-law tail. The observation of bursts (about 1/5 of the bursts) with steeper spectrum at the lower energy part, i.e. below the "synchrotron line of death" [321, 322] is one of the problems that this model faces. The problem is even more severe as in order that the GRB will be radiating efficiently, otherwise the efficiency will be very low, it must be in the fast cooling regime and the relevant low energy spectrum will be ^-1/2 [55, 125]. However, as stressed earlier (see Section IIA1) this problem is not seen in any of the HETE spectrum whose low energy tail is always in the proper synchrotron range with a slope [16] and it might be an artifact of the low energy resolution of BATSE in this energy range [55].

On the other hand the most energetic electrons will always be cooling rapidly (independently of the behavior of the "typical electron"). These electrons emit practically all their energy m_e c² , at their synchrotron frequency. The number of electrons with Lorentz factors ~ is ^1-p and their energy ^2-p. As these electrons cool, they deposit most of their energy into a frequency range ~ _syn() ² and therefore F ^{-p -p/2}. Thus the uppermost part of the spectrum will satisfy:

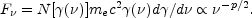(23)

In the intermediate frequency region the spectrum differs between a `slow cooling' if the `typical' electrons with _e,min do not cool on a hydrodynamic time scale and `fast cooling' if they do. The critical parameter that determines if the electrons are cooling fast or slow is _e,c, the Lorentz factor of an electron that cools on a hydrodynamic time scale. To estimate _e,c compare t_syn (Eq. 18) with t_hyd, the hydrodynamic time scale (in the observer's rest frame):

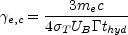(24)

For fast cooling _e,min < _e,c, while _e,min > _e,c for slow cooling. In the following discussion two important frequencies play a dominant role:

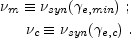(25)

These are the synchrotron frequencies of electrons with e, min and with _e,c.

Fast cooling (_e,c < _e,min): The typical electron is cooling rapidly hence _c < _m. The low frequency spectrum F ^1/3 extends up to _c. In the intermediate range between, _c and _m, we observe the energy of all the cooling electrons. The energy of an electron , and its typical frequency ² the flux per unit frequency is ^{-1 -1/2}. Overall the observed flux, F, is given by:

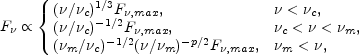(26)

where _{m syn}(_e,min), _{c syn}(_e,c) and F_{, max} is the observed peak flux. The peak flux is at _c F_{, max} N_e P_{, max} / 4 D² (where D is the distance to the source and I ignore cosmological corrections). The power emitted is simply the power given to the electrons, that is _e times the power generated by the shock, dE / dt:

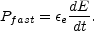(27)

The peak energy emitted (which corresponds to the peak of F) is at _m. The resulting spectrum is shown in Fig. 23.

Slow cooling (_e,c > _e,min): Now only the high energy tail of the distribution (those electrons above _e,c) cools efficiently. The electrons with _e ~ _e,min, which form the bulk of the population, do not cool. Now f ^1/3 up to _m, and F ^-p/2 above _c. In the intermediate region between these two frequencies:

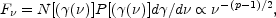(28)

where () is the Lorentz factor for which the synchrotron frequency equals , N[] is the number of electrons with a Lorentz factor and P[] the power emitted by an electron with . Overall one finds:

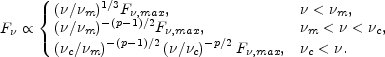(29)

The peak flux is at _m while the peak energy emitted is at _c. The emitted power is determined by the ability of the electrons to radiate their energy:

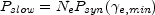(30)

where, N_e is the number of electrons in the emitting region and P_syn(_e,min), the synchrotron power of an electron with _e,min, is given by Eq. 17.

Typical spectra corresponding to fast and slow cooling are shown in Fig. 23. The light curve depends on the hydrodynamic evolution, which in turn determines the time dependence of _m, _c and F_{, max}. The spectra presented here are composed of broken power laws. Granot and Sari [144] present a more accurate spectra in which the asymptotic power law segments are connected by smooth curves. They fit the transitions by [( / _b)^-n₁ + ( / _b)^-n₂]^-1/n. The parameter n estimates the smoothness of the transition with n 1 for all transitions.

Fast cooling must take place during the GRB itself: the relativistic shocks must emit their energy effectively - otherwise there will be a serious inefficiency problem. Additionally the pulse won't be variable if the cooling time is too long. The electrons must cool rapidly and release all their energy. It is most likely that during the early stages of an external shock (that is within the afterglow phase - provided that it arises due to external shocks) there will be a transition from fast to slow cooling [187, 259, 261, 430, 431].

Tavani [401, 402] discusses the synchrotron spectrum from a Gaussian electron distribution and from a Gaussian electron distribution with a high energy tail. As mentioned earlier the Gaussian (thermal) distribution has a typical low frequency ^1/3 spectrum. However, as expected, there is a sharp exponential cutoff at high frequencies. Without a high energy tail this spectrum does not fit the observed GRB spectra of most GRBs (see Section IIA1). Note, however, that it may fit a small subgroup with a NHE [296]. With an electron distribution composed of a Gaussian and an added high energy tail the resulting spectra has the typical ^1/3 component and an additional high energy tail which depends on the electrons power law index. Such a spectra fits several observed GRB spectra [401, 402].

Another variant is the synchrotron spectrum from a power-law electron distribution with 1 < p < 2 [28, 64]. In this case there must be a high energy cutoff _e,max and the `typical' electron's energy corresponds to this upper cutoff. A possible cutoff can arise from Synchrotron losses at the energy where the acceleration time equals to the energy loss time (see e.g. de Jager et al. [73] and the discussion in Section VB):

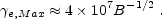(31)

The resulting "typical" Lorentz factor _e,min differs now from the one given by Eq. 22. Bhattacharya [28], Dai and Cheng [64] find that it is replaced with:

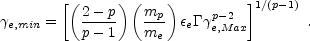(32)

The resulting spectrum is now similar to the one obtained for fast or slow cooling with the new critical frequencies _m given by plugging the result of Eq. 32 into Eq. 26.

3. Synchrotron Self-Absorption

At low frequencies synchrotron self-absorption may take place. It leads to a steep cutoff of the low energy spectrum, either as the commonly known ^5/2 or as ². To estimate the self absorption frequency one needs the optical depth along the line of sight. A simple approximation is: '_' R / where '_' is the absorption coefficient [361]:

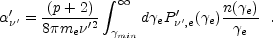(33)

The self absorption frequency _a satisfies: '_'0 R / = 1. It can be estimates only once we have a model for the hydrodynamics and how do R and vary with time [142, 439].

The spectrum below the the self-absorption frequency depends on the electron distribution. One obtains the well known [361], ^5/2 when the synchrotron frequency of the electron emitting the self absorbed radiation is inside the self absorption range. One obtains ² if the radiation within the self-absorption frequency range is due to the low energy tail of electrons that are radiating effectively at higher energies. For this latter case, which is more appropriate for GRB afterglow (for slow cooling with _m < _c) [184, 187, 258, 288]:

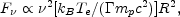(34)

where R is the radius of the radiating shell and the factor k_B T_e / ( m_p c²) describes the degree of electron equipartition in the plasma shock-heated to an internal energy per particle m_p c² and moving with Lorentz factor .

The situation is slightly different for a shock heated fast cooling i.e. if _c < _m [143]. In this case we expect the electron's distribution to be inhomogeneous, as electrons near the shock did not cool yet but electrons further downstream are cool. This leads to a new spectral range _sa < < _sa' with F ^11/8 (see Fig. 23).

Synchrotron self-absorption is probably irrelevant during the GRB itself. Note, however, that under extreme conditions the self absorption frequency might be in the low X-ray and this may explain the steep low energy spectra seen in some bursts. These extreme conditions are needed in order to make the system optically thick to synchrotron radiation but keeping it optically thin to Thompson scattering and pair creation [361]. Self absorption appears regularly during the afterglow and is observed typically in radio emission [142, 184, 187, 430, 439]. The expected fast cooling self-absorbed spectra may arise in the early radio afterglow. So far it was not observed.