8.1. Slowing Down of Relativistic Particles
The cross section for a direct electromagnetic or nuclear interaction between the relativistic particles and the ISM particles is too small to convert efficiently the kinetic energy to radiation. The fireball particles can be slowed down only via some collective interaction such as a collisionless shock. Supernova remnants (SNRs) in which the supernova ejecta is slowed down by the ISM show that collisionless shocks form in somewhat similar circumstances. One can expect that collisionless shocks will form here as well [27, 18].
GRBs are the relativistic analogues of SNRs. In both cases the phenomenon results from the conversion of the kinetic energy of the ejected matter to radiation. Even the total energy involved is comparable. One crucial difference is the amount of ejected mass. SNRs involve a solar mass or more. The corresponding velocity is several thousands kilometers per second, much less than the speed of light. In GRBs, the masses are smaller by several orders of magnitude and with the same energy the matter attains ultra-relativistic velocities. A second crucial difference is that while SNRs result from the interaction of the ejecta with the ISM, GRBs result from internal collisions. The interaction of the ejecta in GRBs with the ISM produces the "afterglow" that follows some GRBs.
The interaction between the SNR ejecta and the ISM takes place on scales of several pc and it is observed for thousands of years. The internal interaction of the relativistic matter in GRBs takes place on a scale of several hundred astronomical units and special relativistic effects reduce the observed time scale to a fraction of a second. The interaction with the ISM that leads to the "afterglow" takes place on a scale of a tenth of a pc. Once more special relativistic effects reduce the observed time scale to several days.
In the following sections I discuss the slowing down of matter due to relativistic shocks. The discussion begins with a general review of relativistic inelastic collisions and continues with the relativistic shock conditions. Then I turn to the radiation processes: synchrotron emission and Inverse Compton. After the general discussion I apply the general results to internal shocks, to external shocks and to the afterglow.
8.1.1. Relativistic Inelastic Collisions
Consider a mass (denoted by the subscript r) that catches up a slower one (denoted s). The two masses collide and merge to form a single mass (denoted m). Energy and momentum conservation yield:
 |
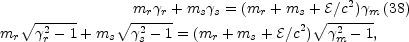(38) |
where 
is the internal
energy generated in the collision (in the rest frame of the merged mass).
There are two interesting limits. First let ms be at
rest:
s
= 1. This is the case in external shocks, or in a shock between
relativistic ejecta and a non-relativistic material
that was ejected from the source before it exploded. Eqs. 39 reveal that
a mass:
 |
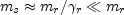(39) |
is needed to yield
m
r
/ 2 and
mr
/ 2. The external mass needed to convert half of the
kinetic energy is smaller than the original mass by a factor of
r
[27,
18].
The second case corresponds to an internal collision between shells
that are moving at different relativistic velocities:
r
s
>> 1. Eqs. 39 yield:
 |
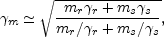(40) |
The internal energy (in the frame of an external observer) of the
merged shell, Eint =
m
, is the difference of
the kinetic energies before and after the collision:
 |
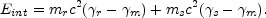(41) |
 |
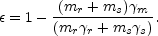(42) |
As can be expected a conversion of a significant fraction of the
initial kinetic energy to internal energy requires that the difference
in velocities between the shells will be significant:
r
>>
s
and that the two masses will be comparable
mr
ms.
Quite often the previous estimates based on the
approximation that the whole shell behaves as a single object are good
enough. However, the time scale between the interaction of different
parts of the shell with the ISM may be relatively long (compared to
the time scale to collect an external mass M /
) and in this
case one has to turn to the hydrodynamics of the interaction. This
calculation takes into account the shocks that form during the collision.
Consider the situation a cold shell (whose internal energy is
negligible compared to the rest mass) that overtakes another
cold shell or moves into the cold ISM. Generally, Two shocks form: an
outgoing
shock that propagates into the ISM or into the external shell, and a
reverse shock that propagates into the inner shell, with a contact
discontinuity between the shocked material (see
Fig. 21). Two quantities determine the shocks'
structure: ,
the Lorentz factor of the motion of the inner shell
(denoted 4) relative to the outer one - or the ISM (denoted 1) and the
ratio between the particle number densities in these regions,
f 
n4 / n1.
 |
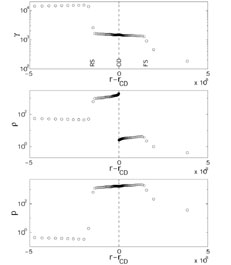Figure 21. The Lorentz factor
|
There are three interesting cases:
(i) Ultra-relativistic shock
( >>
1) with f >
2.
This happens during the early phase of an external shock or during the very
late external shock evolution when there is only a single shock. We
call this configuration "Newtonian" because the reverse
shock is non-relativistic (or mildly relativistic). In this case the
energy conversion takes place in the forward shock: Let
2
be the Lorentz factor of the motion of the shocked
fluid relative to the rest frame of the fluid at 1 (an external
observer for interaction with the ISM and the outer shell in case of
internal collision) and let
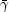3 be the Lorentz factor of
the motion of this fluid relative to the rest
frame of the relativistic shell (4).
 |
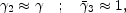(43) |
The particle and energy densities (n, e) in the shocked regions satisfy:
 |
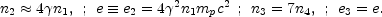(44) |
(ii) Later during the propagation of the shell the density ratio
decreases and f <
2.
Both the forward and the reverse shocks
are relativistic. The shock equations between regions 1 and 2 yield:
[238,
239,
222]:
 |
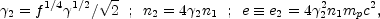(45) |
Similar relations hold for the reverse shock:
 |
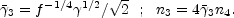(46) |
In addition we have e3 = e and
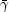3 
( /
2
+ 2 /
) / 2 which
follow from
the equality of pressures and velocity on the contact discontinuity.
Comparable amounts of energy are converted to thermal energy in both
shocks when both shocks are relativistic. But only a negligible
amount of energy is converted to thermal energy in the reverse shock
if it is Newtonian
[233].
(iii) Internal shocks are characterized by
f 1 - both
shells have similar densities, and by a Lorentz factor of order of a
few (2 <
< 10) describing the relative motion of the shells.
In this case, for an adiabatic index (4/3) we have:
 |
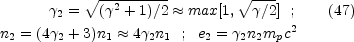(47) |
Both shocks are mildly relativistic and their strength depends on the relative Lorentz factors of the two shells.
8.1.3. Lorentz Factors in Different Emitting Regions
Before concluding this section and turning to the radiation mechanisms
we summarize briefly the different relativistic motions
encountered when considering different emitting regions. The
relativistic shocks are characterized by
sh
that describes
the shock's velocity as well as the "thermal" motion of the shocked
particles. It is measured relative to a rest frame in which the
unshocked material is at rest. The Lorentz factor of the forward shock
is usually different from the Lorentz factor of the reverse shock.
The emitting region - the shocked material - moves relativistically
relative to an observer at rest at infinity. This is
characterized by a Lorentz factor,
E.
Table 8.1.3 summarizes the different values of
sh
and
E
for external and internal shocks and for the afterglow.
| Shock type | E |
sh |
||
| External | Newtonian | Forward | |
|
| Reverse |
|
1 | ||
| Relativistic | Forward |
 3/4 |
3/4 |
|
| Reverse |
3/4 |
-3/4 |
||
| Internal |
|
(int / 2)1/2 ~ a few |
||
| Afterglow |
(t) |
(t) |
||
and
the pressure p in the shocks. There are four
regions: the ISM (region 1), the shocked ISM (region 2), the shocked
shell (region 3) and the unshocked shell (region 4), which are
separated by the forward shock (FS), the contact discontinuity (CD)
and the reverse shock (RS). The initial parameters are the same as in