8.2. Synchrotron Emission from Relativistic Shocks

8.2.1. General Considerations

The most likely radiation process in GRBs is synchrotron emission [240, 18, 222, 103]. The observed low energy spectra provide an indication that this is indeed the case [95, 241].

The parameters that determine synchrotron emission are the magnetic field strength, B, and the electrons' energy distribution (characterized by the minimal Lorentz factor _e,min and the index of the expected power-law electron energy distribution p). These parameters should be determined from the microscopic physical processes that take place in the shocks. However, it is difficult to estimate them from first principles. Instead we define two dimensionless parameters, _B and _e, that incorporate our ignorance and uncertainties [222, 103].

The dimensionless parameter _B measures the ratio of the magnetic field energy density to the total thermal energy e:

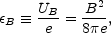(48)

so that, after substituting the shock conditions we have:

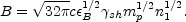(49)

There have been different attempts to estimate _B [224, 240, 226]. We keep it as a free parameter. Additionally we assume that the magnetic field is randomly oriented in space.

The second parameter, _e, measures the fraction of the total thermal energy e which goes into random motions of the electrons:

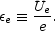(50)

8.2.2. The Electron Distribution

We call consider a "typical" electron as one that has the average _e of the electrons distribution:

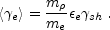(51)

Collisionless acceleration of electrons can be efficient if they are tightly coupled to the protons and the magnetic field by mean of plasma waves [243]. Since the electrons receive their random motions through shock-heating, we assume (following the treatment of non-relativistic shocks) that they develop a power law distribution of Lorentz factors:

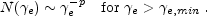(52)

We require p > 2 so that the energy does not diverge at large _e. Since the shocks are relativistic we assume that all the electrons participate in the power-law, not just a small fraction in the tail of the distribution as in the Newtonian case. An indication that this assumption is correct is given by the lower energy spectrum observed in some GRBs [95, 241]. The minimum Lorentz factor, _e,min, of the distribution is related to _e and to the total energy e ~ _sh n m_pc²:

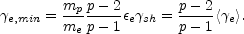(53)

where _sh is the relative Lorentz factor across the corresponding shock.

The energy index p can be fixed by requiring that the model should be able to explain the high energy spectra of GRBs. If we assume that most of the radiation observed in the soft gamma-rays is due to synchrotron cooling, then it is straightforward to relate p to the power-law index of the observed spectra of GRBs, . The mean spectral index of GRBs at high photon energies - 2.25, [84] corresponds to p 2.5. This agrees, as we see later (9.3.2) with the value inferred from afterglow observations (p ~ 2.25). We assume this value of p in what follows. The corresponding ratio that appears in Eq. 53 (p - 2) / (p - 1) equals 1/3 and we have _e,min = 610 _sh.

The shock acceleration mechanisms cannot accelerate the electrons to arbitrary high energy. For the maximal electron's energy, with a corresponding _e,max, the acceleration time equals to the cooling time. The acceleration time is determined by the Larmor radius R_L and the Alfvén velocity v_A [244]:

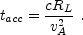(54)

This time scale should be compared with the synchrotron cooling time _e m_e c² / P_syn (in the local frame). Using v_A² _B², Eq. 49 to estimate B and Eq. 57 below to estimate P_syn one finds:

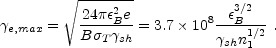(55)

cooling This value is quite large and generally it does not effect the observed spectrum in the soft gamma ray range.

8.2.3. Synchrotron Frequency and Synchrotron Power

The typical energy of synchrotron photons as well as the synchrotron cooling time depend on the Lorentz factor _e of the relativistic electron under consideration and on the strength of the magnetic field (see e.g. [245]). Since the emitting material moves with a Lorentz factor _E the photons are blue shifted. The characteristic photon energy in the observer frame is given by:

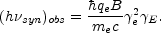(56)

The power emitted by a single electron due to synchrotron radiation in the local frame is:

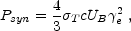(57)

where _T is the Thomson cross section. The cooling time of the electron in the fluid frame is then _e m_e c² / P. The observed cooling time t_syn is shorter by a factor of _E:

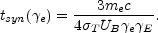(58)

Substituting the value of _e from equation 56 into the cooling rate Eq. 58 we obtain the cooling time scale as a function of the observed photon energy:

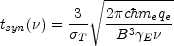(59)

Since _e does not appear explicitly in this equation t_syn at a given observed frequency is independent of the electrons' energy distribution within the shock. This is provided, of course, that there are electrons with the required _e so that there will be emission in the frequency considered. As long as there is such an electron the cooling time is "universal". This equation shows a characteristic scaling of t_syn() ^-1/2. This is not very different from the observed relation T ^-0.4 [102]. However, it is not clear if the cooling time and not another time scale determined the temporal profile.

The cooling time calculated above sets a lower limit to the variability time scale of a GRB since the burst cannot possibly contain spikes that are shorter than its cooling time. Observations of GRBs typically show asymmetric spikes in the intensity variation, where a peak generally has a fast rise and a slower exponential decline (FRED). A plausible explanation of this observation is that the shock heating of the electrons happens rapidly (though episodically), and that the rise time of a spike is related to the heating time. The decay time is then set by the cooling, so that the widths of spikes directly measure the cooling time.

8.2.4. The Integrated Synchrotron Spectrum

The instantaneous synchrotron spectrum of a single electron with an initial energy _e m_e c² is a power law with F ^1/3 up to _syn(_e) and an exponential decay above it. If the electron is energetic it will cool rapidly until it will reach _e,c. This is the Lorentz factor of an electron that cools on a hydrodynamic time scale. For a rapidly cooling electron we have to consider the time integrated spectrum above h_syn(_e,c): F ^-1/2 from _syn(_e,c) up to _syn(_e).

To calculate the overall spectrum due to all the electrons we need to integrate over _e. Our discussion here follows [246]. We consider a power-law electron distribution with a power index p and a minimal Lorentz factor _e,min (see Eq. 52). Overall we expect a broken power law spectrum with a break frequency around the synchrotron frequency of the lowest energy electrons _syn(_e,min). These power law indices depend on the cooling rate. The most energetic electrons will always be cooling rapidly (independently of the behavior of the "typical electron"). Thus the highest spectrum is always satisfy:

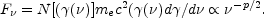(60)

similarly the low energy electrons will always be slow cooling and thus the lowest part of the spectrum will behave like F ^1/3.

For slow cooling we have the instantaneous spectrum: F ^1/3 for the lower part of the spectrum. For the upper part we have

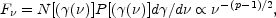(61)

where () is the Lorentz factor for which the synchrotron frequency equals . The most energetic electrons will cool rapidly even when the overall system is in slow cooling. These electrons emit practically all their energy m_e c² , at their synchrotron frequency. Thus the uppermost part of the spectrum will satisfy:

For fast cooling we have F ^-1/2 for the lower part and F ^-p/2 for the upper part. Here at the lower end the least energetic electrons will be cooling slowly even when the typical electron is cooling rapidly. Thus we will have f ^1/3 in the lowest part of the spectrum.

The critical parameter that determines if the electrons are cooling fast or slow is _e,c, the Lorentz factor of an electron that cools on a hydrodynamic time scale. To estimate _e,c we compare t_syn (Eq. 58) with t_hyd, the hydrodynamic time scale (in the observer's rest frame):

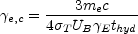(62)

Fast cooling occurs if _e,c < _e,min. All the electrons cool rapidly and the electrons' distribution effectively extends down to _e,c. If _e,c > _e,min only the high energy tail of the distribution (those electrons above _e,c) cool and the system is in the slow cooling regime.

For the GRB itself we must impose the condition of fast cooling: the relativistic shocks must emit their energy effectively - otherwise there will be a serious inefficiency problem. Additionally we won't be able to explain the variability if the cooling time is too long. The electrons must cool rapidly and release all their energy. In this case _e,min > _e,c [103] and all the electrons cool down roughly to _e,c. The observed flux, F, is given by:

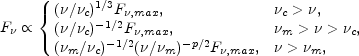(63)

where _{m syn}(_e,min), _{c syn}(_e,c) and F_{, max} is the observed peak flux.

It is most likely that during the latter stages of an external shock (that is within the afterglow phase - provided that it arises due to external shocks) there will be a transition from fast to slow cooling [21, 23, 47, 247, 25]. When _c > _e,min, only those electrons with _e > _c can cool. We call this slow cooling, because the electrons with _e ~ _e,min, which form the bulk of the population, do not cool. Integration over the electron distribution gives in this case:

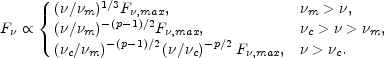(64)

For fast cooling _c < _m. We find that the peak flux is at _c while the peak energy emitted (which corresponds to the peak of F) is at _m. For slow cooling the situation reverses _m < _c. The peak flux is at _m while the peak energy emitted is at _c.

Typical spectra corresponding to fast and slow cooling are shown in Fig. 22. The light curve depends on the hydrodynamic evolution, which in turn determines the time dependence of _m, _c and F_{, max}.

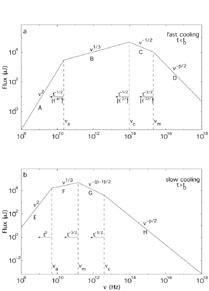Figure 22. Synchrotron spectrum of a relativistic shock with a power-law electron distribution. (a) Fast cooling, which is expected at early times (t < t0). The spectrum consists of four segments, identified as A, B, C, D. Self-absorption is important below a. The frequencies, m, c, a, decrease with time as indicated; the scalings above the arrows correspond to an adiabatic evolution, and the scalings below, in square brackets, to a fully radiative evolution. (b) Slow cooling, which is expected at late times (t > t0). The evolution is always adiabatic. The four segments are identified as E, F, G, H. From [246].

For fast cooling the power emitted is simply the power given to the electrons, that is _e times the power generated by the shock:

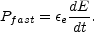(65)

For slow cooling the emitted power is determined by the ability of the electrons to radiate their energy:

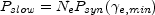(66)

where, N_e is the number of electrons in the emitting region and P_syn(_e,min), the synchrotron power of an electron with _e,min, is given by Eq. 57.