8.5. Radiative Efficiency
The efficiency of a burst depends on three factors: First only the
electrons' energy is available. This yields a factor
e.
Second, if
B <
e there is an
additional factor of min[1,
(B /
e)1/2] if
the IC radiation is not observed. Third, there is a specific Lorentz
factor,
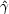e, of
an electron which emits synchrotron (or
IC) radiation in the 100 keV energy band. Therefore, only the energy
radiated by electrons with
e
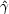e
is observed as soft
-rays.
Assuming a power law electron distribution with an index p = 2.5 (see
[103])
this gives a factor of (e,min /
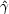e)1/2 (which is valid of
course provided that e,min <
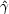e).
The total efficiency is the multiplication
of those three factors and it is given by:
 |
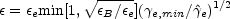(72) |
The efficiency depends first of all on the electrons' energy density
and to a lesser extend on the magnetic energy density. Both should be close
to equipartition in order that the efficiency will be large.
Additionally, in order that there will be photons in the 100 keV range
e,min should be smaller than
.
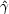However efficient production of soft
-rays
requires that e,min will not be too small compared with
.
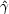This estimate is, of course, different if the observed
-rays are
produced by inverse Compton scattering.