8.6. Internal Shocks

Internal shocks are the leading mechanism for energy conversion and production of the observed gamma-ray radiation. We discuss, in this section, the energy conversion process, the typical radiation frequency and its efficiency.

8.6.1. Parameters for Internal Shocks

Internal shocks take place when an inner shell overtakes a slower outer shell. Consider a fast inner shell with a Lorentz factor _r that collides with a slower shell whose Lorentz factor is _s. If _{r s} ~ then the inner shell will overtake the outer one at:

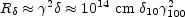(73)

where is the initial separation between the shells in the observer's rest frame and 10 = / 10¹⁰ cm and ₁₀₀ = / 100. Clearly internal shocks are relevant only if they appear before the external shock that is produced as the shell sweeps up the ISM. We show in section 8.7.1 that the necessary condition for internal shocks to occur before the external shock is:

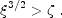(74)

where and are two dimensionless parameters. The parameter, , characterizes the interaction of the flow with the external medium and it is defined in Eq. 92 (see section 8.7.1). The second parameter, , characterizes the variability of the flow:

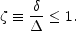(75)

We have seen in section 7.4 that for internal shocks the duration of the burst T / c and the duration of individual spikes T / c. The observed ratio defined in section 2.2 must equal 1 / and this sets 0.01.

The overall duration of a burst produced by internal shocks equals / c. Thus, whereas external shocks require an extremely large value of to produce a very short burst, internal shocks can produce a short burst with a modest value of the Lorentz factor . This eases somewhat the baryon purity constraints on source models. The condition 74 can be turned into a condition that is sufficiently small:

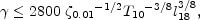(76)

where we have used T = / c and we have defined T₁₀ = T / 10 s and _0.01 = / 0.01. It follows that internal shocks take place in relatively "low" regime. Fig. 23 depicts the regimes in the physical parameter space (, ) in which various shocks are possible. It also depicts an example of a T = / c = 1s line.

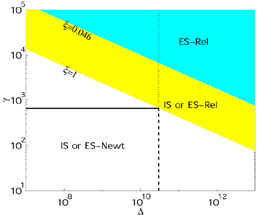Figure 23. Different scenarios in the (in cm) - plane for / = 0.01. Relativistic ES occur for large and large - upper right -above the = 1 line (dark gray and light gray regions). Newtonian ES occur below = 1 - lower left - white region. IS occur, if there are sufficient variation in below the = 2/3 line (light gray and white regions). The equal duration T = 1s curve is shown for Newtonian ES (solid line) a relativistic ES (dotted line) and IS (dashed line). Note that a relativistic ES and an internal shock with the same parameters have the same overall duration T but different temporal substructure depending on . From [232].

Too low a value of the Lorentz factor leads to a large optical depth in the internal shocks region. Using Eq. 27 for R_e, at which the optical depth for Compton scattering of the photons on the shell's electrons equals one, Eq. 73 for R and the condition R_e R we find:

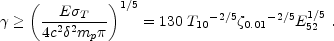(77)

In addition, the radius of emission should be large enough so that the optical depth for e⁺ e^- will be less than unity ( < 1). There are several ways to consider this constraint. The strongest constraint is obtained if one demands that the optical depth of an observed high energy, e.g. 100MeV photon will be less than unity [210, 211]. Following these calculations and using Eq. 73 to express R we find:

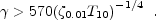(78)

This constraint, which is due to the interaction, is generally more important than the constraint due to Compton scattering: that is > _e.

Eq. 76, and the more restrictive Eq. 78 constrains to a relatively narrow range:

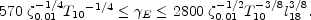(79)

This can be translated to a rather narrow range of emission radii:

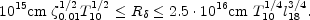(80)

In Fig. 24, we plot the allowed regions in the and parameter space. Using the less restrictive _e limit 77 we find:

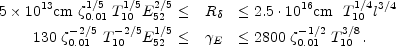Three main conclusions emerge from the discussion so far. First, if the spectrum of the observed photons extends beyond 100 MeV (as was the case in the bursts detected by EGRET [83]) and if those high energy photons are emitted in the same region as the low energy ones then the condition on the pair production, , Eq. 78 is stronger than the condition on Compton scattering Eq. 81. This increases the required Lorentz factors. Second, the Compton scattering limit (which is independent of the observed high energy tail of the spectrum) poses also a lower limit on . However, this is usually less restrictive then the limit. Finally, one sees in Fig. 24 that optically thin internal shocks are produced only in a narrow region in the (, ) plane. The region is quite small if the stronger pair production limit holds. In this case there is no single value of that can produce peaks over the whole range of observed durations. The allowed region is larger if we use the weaker limits on the opacity. But even with this limit there is no single value of that produces peaks with all durations. The IS scenario suggests that bursts with very narrow peaks should not have very high energy tails and that very short bursts may have a softer spectrum.

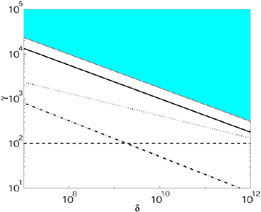Figure 24. Allowed regions for internal shocks in the (in cm), plane. Note that the horizontal axis also corresponds to the typical peak duration, t multiplied by c. Internal shocks are impossible in the upper right (light gray) region. The lower boundary of this region depends on / and are marked by two solid curves, the lower one for = 1 and the upper one for = 0.01. Also shown are = 1 for an observed spectrum with no upper bound (dotted line), = 1 for an observed spectrum with an upper bound of 100 MeV (dashed line) and e = 1 (dashed-dotted). The optically thin internal shock region is above the = 1 curves and below the = 2/3 (solid) lines. From [232].

8.6.2. Physical Conditions and Emission from Internal Shocks

Provided that the different parts of the shell have comparable Lorentz factors differing by factor of ~ 2, the internal shocks are mildly relativistic. The protons' thermal Lorentz factor will be of order of unity, and the shocked regions will still move highly relativistically towards the observer with approximately the initial Lorentz factor . In front of the shocks the particle density of the shell is given by the total number of baryons E / m_p c² divided by the co-moving volume of the shell at the radius R which is 4 R² . The particle density behind the shock is higher by a factor of 7 which is the limiting compression possible by Newtonian shocks (assuming an adiabatic index of relativistic gas, i.e., 4/3). We estimate the pre-shock density of the particles in the shells as: [E / ( m_p c²)] / (4( ²)² ). We introduce _int as the Lorentz factor of the internal shock. As this shock is relativistic (but not extremely relativistic) _int is of order of a few. Using Eq. 48 for the particle density n and the thermal energy density e behind the shocks we find:

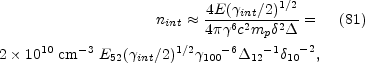(81)

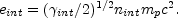(82)

We have defined here ₁₂ = / 10¹² cm. Using Eq. 49 we find:

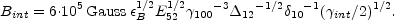(83)

Using Eqs. 49, 51, 56 and 81 we can estimate the typical synchrotron frequency from an internal shock. This is the synchrotron frequency of an electron with a "typical" Lorentz factor:

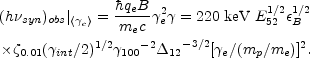(84)

The corresponding observed synchrotron cooling time is:

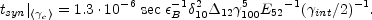(85)

Using Eq. 53 we can express _e,min in terms of _int to estimate the minimal synchrotron frequency:

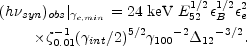(86)

The energy emitted by a "typical electron" is around 220keV. The energy emitted by a "minimal energy" electron is about one order of magnitude lower than the typical observed energy of ~ 100 keV. This should correspond to the break energy of the spectrum. This result seems in a good agreement with the observations. But this estimate might be misleading as both _B and _e might be significantly lower than unity. Still these values of (h _syn)_obs are remarkably close to the observations. One might hope that this might explain the observed lower cutoff of the GRB spectrum. Note that a lower value of _B or _e might be compensated by a higher value of _int. This is advantageous as shocks with higher _int are more efficient (see section 8.6.4).

The synchrotron cooling time at a given frequency (in the observer's frame) is given by:

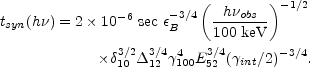(87)

We recover the general trend t_syn (h )^-1/2 of synchrotron emission. However if (as we expect quite generally) this cooling time is much shorter than T_ang it does not determine the width of the observed peaks. It will correspond to the observed time scales if, for example, _B is small. But then the "typical" photon energy will be far below the observed range. Therefore, it is not clear this relation can explain the observed dependence of the width of the bursts on the observed energy.

8.6.3. Inverse Compton in Internal Shocks

The calculations of section 8.4 suggest that the typical Inverse Compton (IC) (actually synchrotron - self Compton) radiation from internal shocks will be at energy higher by a factor _e² then the typical synchrotron frequency. Since synchrotron emission is in the keV range and _e,min m_p / m_e, the expected IC emission should be in the GeV or even TeV range. This radiation might contribute to the prompt very high energy emission that accompanies some of the GRBs [83].

However, if the magnetic field is extremely low: _B ~ 10^-12 then we would expect the IC photons to be in the observed ~ 100 keV region:

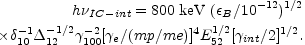(88)

Using Eqs. 71 and 83 we find that the cooling time for synchrotron-self Compton in this case is:

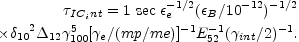(89)

This is marginal. It is too large for some bursts and possibly adequate for others. It could possibly be adjusted by a proper choice of the parameters. It is more likely that if Inverse Compton is important then it contributes to the very high (GeV or even TeV) signal that accompanies the lower energy GRB (see also [250]).

8.6.4. Efficiency in Internal Shocks

The elementary unit in the internal shock model (see section 7.4) is a a binary (two shells) encounter between a rapid shell (denoted by the subscript r) that catches up a slower one (denoted s). The two shells merge to form a single shell (denoted m). The system behaves like an inelastic collision between two masses m_r and m_s.

The efficiency of a single collision between two shells was calculated earlier in section 8.1.1. For multiple collisions the efficiency depends on the nature of the random distribution. It is highest if the energy is distributed equally among the different shells. This can be explained analytically. Consider a situation in which the mass of the shell, m_i is correlated with the (random) Lorentz factor, _i as m_{i i}. Let all the shells collide and merge and only then emit the thermal energy as radiation. Using conservation of energy and momentum we can calculate the overall efficiency:

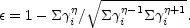(90)

Averaging over the random variables _i, and assuming a large number of shells N we obtain:

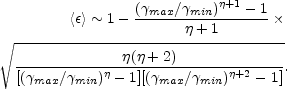(91)

This formula explains qualitatively the numerical results: the efficiency is maximal when the energy is distributed equally among the different shells (which corresponds to = - 1).

In a realistic situation we expect that the internal energy will be emitted after each collision, and not after all the shells have merged. In this case there is no simple analytical formula. However, numerical calculations show that the efficiency of this process is low (less than 2%) if the initial spread in is only a factor of two [32]. However the efficiency could be much higher [33]. The most efficient case is when the shells have a comparable energy but very different Lorentz factors. In this case ( = - 1, and spread of Lorentz factor _max / _min > 10³) the efficiency is as high as 40%. For a moderate spread of Lorentz factor _max / _min = 10, with = - 1, the efficiency is 20%.

The efficiency discussed so far is the efficiency of conversion of kinetic energy to internal energy. One should multiply this by the radiative efficiency, discussed in 8.5 (Eq. 72) to obtain the overall efficiency of the process. The resulting values may be rather small and this indicates that some sort of beaming may be required in most GRB models in order not to come up with an unreasonable energy requirement.

8.6.5. Summary - Internal Shocks

Internal shocks provide the best way to explain the observed temporal structure in GRBs. These shocks, that take place at distances of ~ 10¹⁵ cm from the center, convert two to twenty percent of the kinetic energy of the flow to thermal energy. Under reasonable conditions the typical synchrotron frequency of the relativistic electrons in the internal shocks is around 100 keV, more or less in the observed region.

Internal shocks require a variable flow. The situation in which an inner shell is faster than an outer shell is unstable [251]. The instability develops before the shocks form and it may affect the energy conversion process. The full implications of this instability are not understood yet.

Internal shocks can extract at most half of the shell's energy [32, 33, 69]. Highly relativistic flow with a kinetic energy and a Lorentz factor comparable to the original one remains after the internal shocks. Sari & Piran [20] pointed out that if the shell is surrounded by ISM and collisionless shock occurs the relativistic shell will dissipate by "external shocks" as well. This predicts an additional smooth burst, with a comparable or possibly greater energy. This is most probably the source of the observed "afterglow" seen in some counterparts to GRBs which we discuss later. This leads to the Internal-External scenario [252, 20, 26] in which the GRB itself is produced by an Internal shock, while the "afterglow" that was observed to follows some GRBs is produced by an external shock.

The main concern with the internal shock model is its low efficiency of conversion of kinetic energy to -rays. This could be of order twenty percent under favorable conditions and significantly lower otherwise. If we assume that the "inner engine" is powered by a gravitational binding energy of a compact object (see section 10.1) a low efficiency may require beaming to overcome an overall energy crisis.