


4.2. Sources of Possible Systematic Uncertainty
The absolute calibration of both the SZE and X-ray observations directly affects the distance determinations. In addition to the absolute calibration uncertainty from the observations, there are possible sources of systematic uncertainty that depend on the physical state of the ICM and other sources that can contaminate the cluster SZE emission. Table 1 summarizes the systematic uncertainties in the Hubble constant determined from 30 GHz interferometric SZE observations of a sample of 18 clusters (Reese et al., 2002), but are typical of most SZE experiments. The entries marked with asterisks are expected to average out for a large sample of clusters and include a 1 / 181/2 factor reflecting the 18 clusters used in this work. For detailed discussions of systematics see Birkinshaw (1999) and Reese et al. (2002); Reese et al. (2000).
| Systematic | Effect (%) |
| SZE calibration | ± 8 |
| X-ray calibration | ± 10 |
| NH | ± 5 |
| Asphericity* | ± 5 |
| Isothermality | ± 10 |
| Clumping | -20 |
| Undetected radio sources | ± 12 |
| Kinetic SZE* | ± 2 |
| Primary CMB* | < ± 1 |
| Radio halos | -3 |
| Primary beam | ± 3 |
| +22-30 | |
| * Includes 1 / 181/2 factor for the 18 cluster sample. | |
Most clusters do not appear circular in radio, X-ray, or optical
wavelengths.
Under the assumption of axisymmetric clusters, the combined effect of
cluster asphericity and its orientation on the sky conspires to
introduce a roughly ± 20% random uncertainty in
H0 determined from one galaxy cluster
(Hughes &
Birkinshaw, 1998).
When one considers a
large, unbiased sample of clusters, with random orientations, the
errors due to imposing a spherical model are expected to cancel,
resulting in a precise determination of H0. Numerical
simulations
using triaxial  models support this assumption
(Sulkanen, 1999).
models support this assumption
(Sulkanen, 1999).
Departures from isothermality in the cluster atmosphere may result in a large error in the distance determination from an isothermal analysis. The ROSAT band is fairly insensitive to temperature variations, showing a ~ 10% change in the PSPC count rate for a factor of 2 change in temperature for Te > 1.5 keV gas (Mohr et al., 1999). A mixture of simulations and studies of nearby clusters suggests a 10% effect on the Hubble parameter due to departures from isothermality (e.g., Inagaki et al., 1995; Roettiger et al., 1997).
Clumping of the intracluster gas is a potentially serious source of systematic error in the determination of the Hubble constant. Unresolved clumps in an isothermal intracluster plasma will enhance the X-ray emission by a factor C2, where
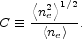 |
(7) |
If significant substructure exists in galaxy clusters, the cluster
generates more X-ray emission than expected from a uniform ICM,
leading to an underestimate of the angular-diameter distance
(DA
 Sx0-1) and therefore an overestimate of the
Hubble
parameter by a factor C2. Unlike orientation bias, which
averages down for a large sample of clusters, clumping must be
measured in each cluster or estimated for an average cluster. There
is currently no observational evidence of significant clumping in
galaxy clusters. If clumping were significant and had large variations
from cluster to cluster, we might expect larger scatter than is seen
in the Hubble diagrams from SZE and X-ray distances
(Fig. 6). In addition, the agreement
between SZE (e.g.,
Grego et al., 2001)
and X-ray (e.g.,
Mohr et al., 1999)
determined gas fractions from galaxy clusters also suggests that
clumping is not a large effect.
Sx0-1) and therefore an overestimate of the
Hubble
parameter by a factor C2. Unlike orientation bias, which
averages down for a large sample of clusters, clumping must be
measured in each cluster or estimated for an average cluster. There
is currently no observational evidence of significant clumping in
galaxy clusters. If clumping were significant and had large variations
from cluster to cluster, we might expect larger scatter than is seen
in the Hubble diagrams from SZE and X-ray distances
(Fig. 6). In addition, the agreement
between SZE (e.g.,
Grego et al., 2001)
and X-ray (e.g.,
Mohr et al., 1999)
determined gas fractions from galaxy clusters also suggests that
clumping is not a large effect.
4.2.2. Possible SZE Contaminants
Undetected point sources near the cluster mask the central decrement,
causing an underestimate in the magnitude of the decrement and
therefore an underestimate of the angular diameter distance. Point
sources in reference fields and for interferometers, the complicated
synthesized beam shapes, may cause overestimates of the angular
diameter distance. Massize clusters typically have central dominant
(cD) galaxies, which are often radio bright. Therefore, it is likely
that there is a radio point source near the center of each cluster.
Typical radio sources have falling spectra, roughly

 1,
where S
1,
where S

 -
- . At 30 GHz, possible
undetected
point sources just below the detection threshold of the observations
introduce a ~ 10% uncertainty.
. At 30 GHz, possible
undetected
point sources just below the detection threshold of the observations
introduce a ~ 10% uncertainty.
Cluster peculiar velocities with respect to the CMB introduce an additional CMB spectral distortion known as the kinetic SZE (see Section 2.2). For a single isothermal cluster, the ratio of the kinetic SZE to the thermal SZE is
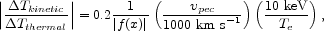 |
(8) |
where
 pec is
the peculiar velocity along the line of sight. At
low frequencies (Rayleigh-Jeans regime),
f (x)
pec is
the peculiar velocity along the line of sight. At
low frequencies (Rayleigh-Jeans regime),
f (x)  -2 and the kinetic SZE
is ~ 10% of the thermal SZE. Recent observational evidence
suggests a typical one-dimensional rms peculiar velocity of ~ 300
km s-1
(Watkins, 1997),
and recent simulations found similar results
(Colberg et al.,
2000).
In general, the kinetic effect is
-2 and the kinetic SZE
is ~ 10% of the thermal SZE. Recent observational evidence
suggests a typical one-dimensional rms peculiar velocity of ~ 300
km s-1
(Watkins, 1997),
and recent simulations found similar results
(Colberg et al.,
2000).
In general, the kinetic effect is
 10%
that of the thermal SZE, except near the thermal null at ~ 218 GHz
where the kinetic SZE dominates (see
Fig. 2).
Cluster peculiar velocities are randomly distributed, so when averaged
over an ensemble of clusters, the effect from peculiar velocities
should cancel.
10%
that of the thermal SZE, except near the thermal null at ~ 218 GHz
where the kinetic SZE dominates (see
Fig. 2).
Cluster peculiar velocities are randomly distributed, so when averaged
over an ensemble of clusters, the effect from peculiar velocities
should cancel.
CMB primary anisotropies have the same spectral signature as the
kinetic SZE. The effects of primary anisotropies on cluster distances depend
strongly on the beam size of the SZE observations and the typical
angular scale of the clusters being observed (nearby versus distant
clusters); the CMB effects on the inferred Hubble
constant should average out over an ensemble of clusters. Recent BIMA
observations provide limits on primary anisotropies on scales of a few
arcminutes
(Dawson et al.,
2001;
Holzapfel et
al., 2000).
On these scales, CMB primary anisotropies are an unimportant
( 1%) source of
uncertainty. For nearby clusters, or for searches for distant
clusters using beams larger than a few arcminutes, the intrinsic CMB
anisotropy must be considered. The unique spectral signature of the
thermal SZE can be used to separate it from primary CMB anisotropy.
However, it will not be possible to separate primary CMB anisotropies
from the kinetic SZE without relying on the very small spectral
distortions of the kinetic SZE due to relativistic effects.
1%) source of
uncertainty. For nearby clusters, or for searches for distant
clusters using beams larger than a few arcminutes, the intrinsic CMB
anisotropy must be considered. The unique spectral signature of the
thermal SZE can be used to separate it from primary CMB anisotropy.
However, it will not be possible to separate primary CMB anisotropies
from the kinetic SZE without relying on the very small spectral
distortions of the kinetic SZE due to relativistic effects.
The SZE may be masked by large-scale diffuse nonthermal radio emission
in clusters of galaxies, known as radio halos. If present, radio halos
are located at the cluster centers, have sizes typical of galaxy
clusters, and have a steep radio spectrum
(
 1 - 3;
Hanish 1982;
Moffet &
Birkinshaw 1989;
Giovannini et
al. 1999;
Kempner &
Sarazin 2001).
Because halos are rare, little is known about their nature and origin, but
they are thought to be produced by synchrotron emission from an
accelerated or reaccelerated population of relativistic electrons (e.g.,
Schlickeiser
et al., 1987;
Jaffe, 1977;
Roland, 1981;
Dennison, 1980).
Conservative and simplistic modeling of the
possible effects of these halos implies a ~ 3% overestimate on
the inferred Hubble parameter from radio halos
(Reese et al.,
2002).
Reese et al. (2002)
show Very Large Array NVSS contours overlaid on 30 GHz
interferometric SZE images, suggesting that radio halos have little
impact on SZE observations and therefore on SZE/X-ray distances.
1 - 3;
Hanish 1982;
Moffet &
Birkinshaw 1989;
Giovannini et
al. 1999;
Kempner &
Sarazin 2001).
Because halos are rare, little is known about their nature and origin, but
they are thought to be produced by synchrotron emission from an
accelerated or reaccelerated population of relativistic electrons (e.g.,
Schlickeiser
et al., 1987;
Jaffe, 1977;
Roland, 1981;
Dennison, 1980).
Conservative and simplistic modeling of the
possible effects of these halos implies a ~ 3% overestimate on
the inferred Hubble parameter from radio halos
(Reese et al.,
2002).
Reese et al. (2002)
show Very Large Array NVSS contours overlaid on 30 GHz
interferometric SZE images, suggesting that radio halos have little
impact on SZE observations and therefore on SZE/X-ray distances.
Imprecisely measured beam shapes affect the inferred central
decrements and therefore affect the Hubble constant. For
interferometric observations, the primary beam is determined from
holography measurements. Conservative and simple modeling of the
effects of the primary beam suggests that the effect on the Hubble
constant is a few percent
( 3%) at most. In
theory, this is a
controllable systematic with detailed measurements of beam shape and
is currently swamped by larger potential sources of systematic
uncertainty.
3%) at most. In
theory, this is a
controllable systematic with detailed measurements of beam shape and
is currently swamped by larger potential sources of systematic
uncertainty.