4.1. Kochanek's time delay formulation
The system PG1115+080 illustrates another of the major
difficulties in time delay measurements of H0. The
mathematics is simpler if
we diagonalize the magnification matrix and introduce two dimensionless
quantities, the convergence
and the shear
.
 |
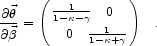(4.1) |
The convergence is the two-dimensional Laplacian of the two-dimensional potential,
 |
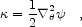(4.2) |
and is therefore proportional to the surface mass density.
For zero shear, a convergence of unity gives infinite magnification in both directions. For zero convergence (which means zero surface density), a shear of unity gives infinite stretching in one direction. For a point mass there is unit shear everywhere on its Einstein ring.
Kochanek (2002; present proceedings) has shown that with these definitions we can write an expression for the difference in time delay between two images in a circularly symmetric system that depends to first order only upon the positions of the images with respect to the lens and the convergence averaged over the annulus bracketted by the two images.
 |
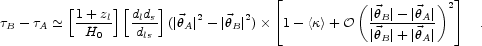(4.3) |
For power law density profiles,
~
r-
, we have
 |
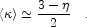(4.4) |
Notice that if
= 2, as would hold for an isothermal sphere, the
average value of the convergence is one half. As
3, approaching the
central concentration for a point mass,
<>
0 and the predicted
time delay is twice as long as in the isothermal case.