4.2. The mass sheet degeneracy

Kochanek's parameterization illuminates two different difficulties in measuring H₀ from time delays. Figure 2 shows PG1115+080 and its immediate surroundings. A fit of our simple model to the image positions indicates that the source of the tide lies along a line passing through the lensing galaxy and the upper right corner of the figure. At the cost of one additional parameter, we can substitute a second isothermal sphere for the tidal shear. This very much improves the fit, and the derived position is coincident with the small group of galaxies to the upper right of the lensed system. The inferred velocity dispersion for the second isothermal sphere is 375 km/s [Schechter et al. (1997)], typical of a small group. The observation of a group at the position "predicted" by the simple model inspires confidence in it.

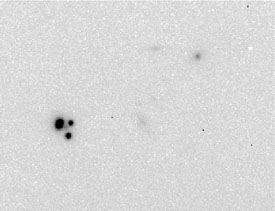Figure 2. The quadruple lens PG1115+080, observed with the Baade 6.5-m telescope. The small group of galaxies to the upper right lies very close to the position predicted from the positions of the four quasar images. It lies at the same redshift as the lensing galaxy.

But if the group is isothermal, it has a convergence associated with it - in this case approximately 10%. This decreases the predicted time delay by 10%. Small numbers make measurement of the actual velocity dispersion difficult, but it is consistent [Tonry (1998)] with the tidal estimate. Many of the quadruple lenses live in groups and clusters with convergences at the position of the lens of 10, 20 and even 30%. The corrections are substantial, and we must wonder whether we have got the cluster convergence correct. Two of the systems in figure 1, Q0957+561 and RXJ0911+0554, have inferred convergences in the 20 - 30% range. This is a manifestation of a difficulty more generally known as the mass sheet degeneracy ([Gorenstein, Shapiro, & Falco (1988)]; [Saha (2000)]). There is no way of knowing (from deflections and distortions) whether or not a mass sheet is present, but it affects the predicted time delays by changing the mean convergence.