


3.2. Modeling the lens
The previous subsection illustrates the power of mathematics:
an enormous amount of interesting astrophysics can be swept under the
rug of a single function, the two dimensional gravitational potential,
 (
( ). If we knew
). If we knew
 a
priori we would long
since have measured the Hubble constant. Instead we must construct
models for our potentials, adjusting them to fit whatever observations
can be brought to bear.
[Williams & Saha (2000)]
have developed a method for modeling lenses that avoids making detailed
assumptions
about the shape of the lensing potential (see also SAHA
& WILLIAMS' contribution to the present proceedings), at the
price of
non-uniqueness. The present author takes the view that we know
something about galaxy potentials and therefore would do well to start
by assuming lensing galaxies are much like nearby galaxies.
a
priori we would long
since have measured the Hubble constant. Instead we must construct
models for our potentials, adjusting them to fit whatever observations
can be brought to bear.
[Williams & Saha (2000)]
have developed a method for modeling lenses that avoids making detailed
assumptions
about the shape of the lensing potential (see also SAHA
& WILLIAMS' contribution to the present proceedings), at the
price of
non-uniqueness. The present author takes the view that we know
something about galaxy potentials and therefore would do well to start
by assuming lensing galaxies are much like nearby galaxies.
A model which is both very simple and very useful is the singular isothermal sphere in the presence of an external tide,
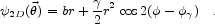 |
(3.7) |
The leading (monopole) term is the projection of the
isothermal's potential. In our case the strength of the isothermal is
parameterized by b, the radius of its Einstein ring. The tidal term
is a quadrupole, and is parameterized by a dimensionless strength,
 , and an
orientation
, and an
orientation

 . Note
that here we represent angular position on the sky,
. Note
that here we represent angular position on the sky,
 , in terms
of polar coordinates r and
, in terms
of polar coordinates r and
 , with r
measured in radians.
, with r
measured in radians.
The singular isothermal sphere gives the flat rotation curves characteristic of nearby galaxies. A substantial fraction of quadruple gravitational lenses are the result of strong tides from a group or cluster of galaxies of which the lens is a member. In the absence of these tides the lenses would produce only double images. The intrinsic flattening of the lensing galaxy also produces a quadrupole term (which has a different radial dependence), but the tidal contribution is usually considerably larger.
Our simple model does great injustice to the complexity of individual lenses, but complexity is a luxury we cannot afford. A parameterized model can have at most as many parameters as the available observable quantities and we are quite limited. The numbers of observables are summarized in table 2. Delay is a scalar, deflection is a two dimensional vector and the symmetric distortion matrix has three independent elements. We have subtracted one deflection from our available constraints because we do not know the position of the source. Likewise we subtract one distortion because we do not know the size and shape of our source (taking it to be elliptical). By the same argument we subtract one delay because we do not know the absolute time at which some event used to calculate delays actually occurred. In the case of delays we subtract a second delay because we need it to calculate the Hubble constant. It cannot be used both to constrain our model and to give H0.
| Delays: | 1 × [#images - 2] |
| Deflections: | 2 × [#images - 1] |
| Distortions: | 3 × [#images - 1] |
| (or for unresolved sources) | |
| magnifications: | 1 × [#images - 1] |
The situation is even worse if the images are not resolved by our telescopes. In such cases we measure only the fluxes of the images and get only one number from each distortion rather than three. Consider the case of a lensed quasar with two unresolved images. After discounting for the unknown properties of the source and reserving one delay for measuring H0 we have only three constraints for our model. Using even our very simple model we are guaranteed a perfect fit, with no additional degrees of freedom left to check goodness of fit.
With no sanity check on our model, such doubles can be used only with extreme caution. Something might be amiss and we would have no way of knowing it. Moreover we cannot add additional parameters (allowing, for example, for the shape of the galaxy) because we have exhausted our supply of constraints. Four of the nine systems in figure 1 are just such doubles: B1600+43, HE2149-2745, SBS1520+53 and HE1104-1805.
The situation is slightly improved for four image systems. It is likewise slightly improved if there are multiple sources, as is sometimes the case for radio AGN. In constructing a list of major difficulties faced in measuring H0, the first would be the paucity of constraints.