6. THE BARYON DENSITY FROM THE CBR

Some 400 kyr after BBN has ended, when the Universe has expanded and cooled sufficiently so that the ionized plasma of protons, alphas, and electrons combines to form neutral hydrogen and helium, the CBR photons are set free to propagate throughout the Universe. Observations of the CBR today reveal the anisotropy spectrum of temperature fluctuations imprinted at that early epoch. The so-called acoustic peaks in the temperature anisotropy spectrum arise from the competition between the gravitational potential and the pressure gradients. An increase in the baryon density increases the inertia of the baryon - photon fluid shifting the locations and the relative heights of the acoustic peaks. In Figure 6 are shown three sets of temperature anisotropy spectra for cosmological models which differ only in the choice of the baryon density parameter _B. Also shown in Figure 6 are the WMAP data from [Bennett et al. (2003)]. It is clear from Figure 6 that the CBR provides a very good baryometer - independent of that from SBBN and primordial deuterium. Based on the WMAP data alone, [Barger et al. (2003a)] find that the best fit value for the density parameter is ₁₀ = 6.3 (_B = 0.023) and that the 2 range extends from ₁₀ = 5.6 to 7.3 (0.020 _B 0.026). This is in excellent (essentially perfect!) agreement (as it should be) with the CBR-only result of [Spergel et al. (2003)]. More importantly, as may be seen clearly in Figure 7 (courtesy of D. Marfatia), this independent constraint on the baryon density parameter, sampled some 400 kyr after BBN, is in excellent agreement with that from SBBN (see Section 5), providing strong support for the standard model of cosmology.

Figure 6. The CBR temperature fluctuation anisotropy spectra for three choices of the baryon density parameter B = 0.018, 0.023, 0.028, in order of increasing height of the first peak. Also shown are the WMAP data points.

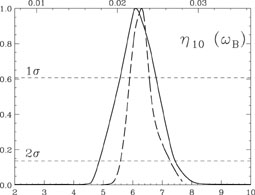Figure 7. The normalized likelihood distributions for the baryon density parameter 10 derived from SBBN and the primordial abundance of deuterium (solid curve; see Section 4.1) and from the CBR using WMAP data alone (dashed curve). The bottom horizontal axis is the baryon-to-photon ratio parameter 10; the top axis is the baryon density parameter B = B h2.

The independent determination of the baryon density parameter by the CBR reinforces the tension between SBBN and the relic abundances of ⁴He and ⁷Li inferred from the observational data (see Section 5). In the context of SBBN, the slightly higher best value of from the WMAP data (compared to that from D plus SBBN) increases the expected primordial abundances of ⁴He and ⁷Li (see Figure 1), widening the gaps between the SBBN predictions and the data. Keeping in mind the observational and theoretical difficulties in deriving the primordial abundances from the data, it is nonetheless worthwhile to explore a class of nonstandard alternatives to the standard model of cosmology in which the early Universe expansion rate is modified (S 1, N 3).