


Since the early universe is hot and dense, interactions among the various particles present are rapid and equilibrium among them is established quickly. But, as the universe expands and cools, there are departures from equilibrium; these are at the core of the most interesting themes of our story.
2.1. An Early Universe Chronology
At temperatures above a few MeV, when the universe is tens of
milliseconds old, interactions among photons, neutrinos, electrons,
and positrons establish and maintain equilibrium
(T =
T
=
T =
Te). When the temperature drops below a few MeV the
weakly interacting neutrinos decouple, continuing to cool and dilute
along with the expansion of the universe
(T
=
Te). When the temperature drops below a few MeV the
weakly interacting neutrinos decouple, continuing to cool and dilute
along with the expansion of the universe
(T
 a-1,
n
a-1,
n
 T
T 3,
and
3,
and 

 T
T 4).
4).
2.1.1. Neutron - Proton Interconversion
Up to now we haven't considered the baryon (nucleon) content of the universe. At these early times there are neutrons and protons present whose relative abundance is determined by the usual weak interactions.
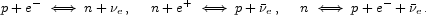 |
(24) |
As time goes by and the universe cools, the lighter protons are favored
over the heavier neutrons and the neutron-to-proton ratio decreases,
initially as n / p
 exp
(-
exp
(-  m /
T), where
m /
T), where
 m = 1.29
MeV is the neutron-proton mass difference. As the temperature drops
below roughly 0.8 MeV, when the universe is roughly one second old,
the rate of the two-body collisions in eq. 24 becomes
slow compared to the universal expansion rate and deviations from
equilibrium occur. This is often referred to as "freeze-out", but
it should be noted that the n / p ratio continues to
decrease as the
universe expands, albeit at a slower rate than if the ratio tracked
the exponential. Later, when the universe is several hundred seconds
old, a time comparable to the neutron lifetime
(
m = 1.29
MeV is the neutron-proton mass difference. As the temperature drops
below roughly 0.8 MeV, when the universe is roughly one second old,
the rate of the two-body collisions in eq. 24 becomes
slow compared to the universal expansion rate and deviations from
equilibrium occur. This is often referred to as "freeze-out", but
it should be noted that the n / p ratio continues to
decrease as the
universe expands, albeit at a slower rate than if the ratio tracked
the exponential. Later, when the universe is several hundred seconds
old, a time comparable to the neutron lifetime
( n = 885.7 ±
0.8 sec.), the n / p ratio resumes falling exponentially:
n / p
n = 885.7 ±
0.8 sec.), the n / p ratio resumes falling exponentially:
n / p  exp(- t /
exp(- t /  n).
Notice that the n/p ratio at BBN depends on
the competition between the weak interaction rates and the early
universe expansion rate so that any deviations from the standard
model (e.g.
n).
Notice that the n/p ratio at BBN depends on
the competition between the weak interaction rates and the early
universe expansion rate so that any deviations from the standard
model (e.g. 

 +
+
 X)
will change the relative numbers of neutrons and protons available for
building more complex nuclides.
X)
will change the relative numbers of neutrons and protons available for
building more complex nuclides.
At the same time that neutrons and protons are interconverting,
they are also colliding among themselves to create deuterons:
n + p
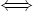 D +
D +
 . However,
at early times when the density and average energy of the CMB photons is
very high, the newly-formed deuterons find themselves bathed in
a background of high energy gamma rays capable of photodissociating
them. As we shall soon see, there are more than a billion photons
for every nucleon in the universe so that before a neutron or a
proton can be added to D to begin building the heavier nuclides,
the D is photodissociated. This bottleneck to BBN beginning in
earnest persists until the temperature drops sufficiently so that
there are too few photons energetic enough to photodissociate the
deuterons before they can capture nucleons to launch BBN. This
occurs after e± annihilation, when the universe
is a few minutes old and the temperature has dropped below 80 keV (0.08
MeV).
. However,
at early times when the density and average energy of the CMB photons is
very high, the newly-formed deuterons find themselves bathed in
a background of high energy gamma rays capable of photodissociating
them. As we shall soon see, there are more than a billion photons
for every nucleon in the universe so that before a neutron or a
proton can be added to D to begin building the heavier nuclides,
the D is photodissociated. This bottleneck to BBN beginning in
earnest persists until the temperature drops sufficiently so that
there are too few photons energetic enough to photodissociate the
deuterons before they can capture nucleons to launch BBN. This
occurs after e± annihilation, when the universe
is a few minutes old and the temperature has dropped below 80 keV (0.08
MeV).
Once BBN begins in earnest, neutrons and protons quickly combine to form D, 3H, 3He, and 4He. Here, there is another, different kind of bottleneck. There is a gap at mass-5; there is no stable mass-5 nuclide. To jump the gap requires 4He reactions with D or 3H or 3He, all of which are positively charged. The coulomb repulsion among these colliding nuclei suppresses the reaction rate ensuring that virtually all of the neutrons available for BBN are incorporated in 4He (the most tightly bound of the light nuclides), and also that the abundances of the heavier nuclides are severely depressed below that of 4He (and even of D and 3He). Recall that 3H is unstable and will decay to 3He. The few reactions which manage to bridge the mass-5 gap mainly lead to mass-7 (7Li, or 7Be which later, when the universe has cooled further, will capture an electron and decay to 7Li); the abundance of 6Li is below that of the more tightly bound 7Li by one to two orders of magnitude. There is another gap at mass-8. This absence of any stable mass-8 nuclides ensures there will be no astrophysically interesting production of heavier nuclides.
The primordial nuclear reactor is short-lived, quickly encountering an energy crisis. Because of the falling temperatures and the coulomb barriers, nuclear reactions cease rather abruptly when the temperature drops below roughly 30 keV, when the universe is about 20 minutes old. As a result there is "nuclear freeze-out" since no already existing nuclides are destroyed (except for those that are unstable and decay) and no new nuclides are created. In ~ 1000 seconds BBN has run its course.