4. The total mass to HI gas mass ratio

Since hydrogen is the most abundant element in stars and galaxies we might expect that its distribution across a galaxy provides information relevant for the theories of galactic evolution. A very simple theory of the chemical evolution of galaxies (Searle and Sargent, 1972) predicts that the abundance of a heavy element in a given volume element depends on the ratio of total mass to gas mass in the following way:

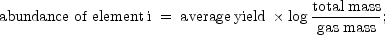(1)

the yield is the ratio of the rate at which heavy elements are produced by nucleosynthesis and ejected into the interstellar gas to the net rate at which hydrogen is removed from the interstellar gas by star formation. More elaborate theories, like those of Talbot and Arnett (1975), Lynden-Bell (1975) and those outlined by Audouze and Tinsley (1976), predict similar relationships between these quantities. If radial mixing is not too important inside a galaxy we can replace the ratio total mass to gas mass by the ratio of local mass surface densities: _M(R) and _G(R) for mass and gas mass respectively. Not much is known about the average yield (the average is a time average from t = 0 until the present epoch). In principle we can obtain information on the abundances from the line strength ratios in HII regions at different radii; the ratio _M(R) / _G(R) can, to some extent, be estimated from 21-cm line observations. In this section we present some information on _M(R) / _HI(R), where _HI(R) is the mass surface density of neutral hydrogen, and we compare these results with available data on line strength ratios.

a) _M(R) / _HI(R)

For 14 galaxies in our sample the radial distribution of an, has been determined from the 21 cm maps by averaging in annuli over the azimuthal direction. The width of these annuli is usually taken to be the size of the synthesized beam. We have corrected to face-on values by a multiplication with the cosine of the inclination. Note that these results are not corrected for optical depth effects. As in the case of rotation curves, also the determination of _HI(R) is hampered by the presence of deviations from axial symmetry in spiral galaxies; for each type of deviation we have followed the same procedures as in the case of rotation curves (see chapter 6). Even more serious is the beamsmoothing in the central parts, and this results in practice in an overestimate of _HI in the centre (cf. chapter 3). The results for _M(R) / _HI(R) are, obviously, even more uncertain.

In Fig. 7 we present the curves of _M(R) / _HI(R) for various galaxies. The curves can be divided in two parts: a gradually declining inner part and a roughly flat outer part. For the galaxies with large scale asymmetries this outer part is actually not reached. In addition to the deviations from axial symmetry another problem arises here: for nearly face-on galaxies the inclination correction for the velocities is large and hence _M is uncertain. This problem is illustrated for the case of M51 in Fig. 7b. The lower curve of M51 is based on an inclination of 35° (the one adopted by Segalovitz, 1976), the upper curve is based on an inclination of 20° (cf. Tully, 1974).

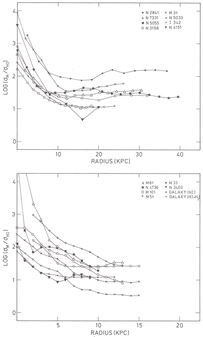Figure 7. Radial variation of the total mass to HI gas mass surface density ratio in various galaxies. M has been taken from Fig. 2 of chapter 6; HI has been calculated from averages over the azimuthal direction of the HI column density distributions, multiplied by cos i; no corrections for optical depth have been applied.

The contributions of gaseous components other than HI to _G(R) are unknown. For our Galaxy an estimate for the contribution of _H to _G can be derived from the CO observations (see Gordon and Burton, 1976). The lack of knowledge about the conversion factor from CO-abundance to H₂ abundance, however, makes such an estimate uncertain. In Fig. 8 we present the variation in _M(R), _HI(R) and _H2(R) in our Galaxy. Since HI and H₂ are the main contributors to the gas mass we tentatively conclude that _M / _G is roughly constant beyond R = 5 kpc. Note that the contribution of H₂ dominates in the inner parts. In our Galaxy there is a fair agreement between the radial distributions of molecules and of HII regions, but the HI extends much farther out (cf. Burton, 1976). In external galaxies the radial distribution of HII-regions is also more concentrated to the inner parts than is the HI distribution It might be conjectured that, similar to our Galaxy, the ratio of _M(R) / _G(R) remains more or less constant beyond about one-third of the optical radius, but we must again emphasize that the uncertainty in the contribution of _H2 to _G is quite large.

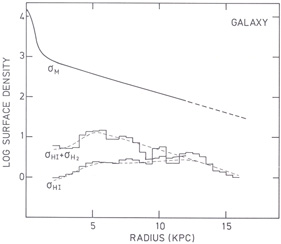Figure 8. Radial variation of mass and gas mass surface densities in our Galaxy. The histograms are adapted from Gordon and Burton (1976). The dashed lines have been used to calculate the M / H curves of our Galaxy in Fig. 7.

b) Variation of _M / _G with type and size

We assume for the moment that the ratio _M(R) / _G(R) is indeed constant in the outer parts of galaxies and that _G(R) is dominated there by _HI(R). The value of this ratio seems to correlate with V_m, as can be seen in Fig. 9. Two difficulties arise in the interpretation of this figure: 1) the inclination, and therefore _M, might be in error for the nearly face-on galaxies; 2) part of the mass may not be distributed in a disk. If these difficulties are not too important, we conclude that galaxies with large V_m have a high _M / _G in the outer parts, while galaxies with smaller V_m have a low _M / _G.

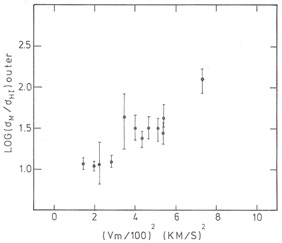Figure 9. Mass to gas mass ratio, M / HI, in the outer parts vs mean rotation velocity Vm. The error bars represent the variation in the nearly flat part of the M / HI-curves in Fig. 7.

Because our sample is small, we do not know whether the correlation in Fig. 9 is a chance coincidence. We can, however, test this correlation by noting that, if _M / _HI is constant, the integrated values M_T / M_H should also give us to some extent the value of this constant. In Fig. 10 we present the values of M_T / M_H as function of Vo, the halfwidth of the 21 cm integral profile, for the sample of galaxies discussed by Shostak (1978). M_T / M_H in this case is derived from integral properties, and is therefore not entirely comparable with the _M / _HI discussed above. Nevertheless, it is clear that there are no galaxies with high V_o and, low M_T / M_H. This result also indicates that in galaxies with high V_m the gas to mass ratio is lower than in galaxies with low V_m.

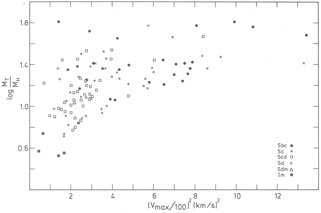Figure 10. Total mass to hydrogen mass ratio vs Vo (half the width of the HI profile divided by sin i) from single dish data by Shostak (1978).

1) The absence of HI in galaxies with bulges is reminiscent to the lack of HI in elliptical galaxies. Perhaps a hot galactic wind is present which keeps the bulge clean of the gas shed from evolving stars (see Faber and Gallagher, 1976).

2) Star formation might play an important role too, but it is not clear which mechanism is responsible for star formation. The fashionable idea that the star formation is triggered by (stationary Lin-Shu) density waves (cf. Oort, 1974; Jensen, Strom and Strom, 1976) might not be adequate to explain the constant value of _M / _G in our Galaxy if the star formation rate is proportional to the difference in angular velocity of the gas and that of the wave i.e. proportional to ( - _p). This mechanism seems also inadequate to explain the absence of gas in the central parts of the multi-armed spiral NGC 2841 (cf. chapter 4.6).

3) For later type galaxies, which have a higher content of population I material, the contribution of molecules may be so high that _M / _G remains constant even though _M / _HI is increasing towards the centre. Quantitative estimates of the contribution of molecules to _G in these galaxies are necessary to test this possibility.

c) Comparison with abundance determinations

For a few galaxies data are available on the strength of the emission lines of several HII regions (see review by Webster, 1977). In Fig. 11 we have presented the data on log [OIII] / H versus radius for five galaxies in our sample, taken from Smith (1975) and Rubin, Kumar and Ford (1972) (we have averaged the data of Rubin et al. by taking means of 4 points at adjacent radii). This line strength ratio increases with radius. Various theoretical studies indicate that this, and similar systematic radial variations in other line strength ratios, can be explained by a decrease of the heavy element abundance with radius (Searle, 1971; Shields and Tinsley, 1976; Sarazin, 1976). Recently Churchwell et al. (1977) reported a systematic variation of the temperature of galactic HII regions across the Galaxy which they interpret as due to an abundance gradient; this result may not be significant in view of the complications in the analysis of radio recombination line data (cf. Lockman and Brown, 1978). Although the amplitude of the abundance gradients depends almost entirely on the assumed HII region models, most authors seem to agree that such gradients exist.

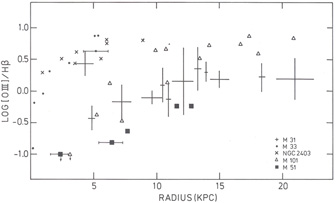Figure 11. Radial variation of the [OIII] / H line strength ratio in various galaxies. The data for M31 are averages of 4 points, adjacent in radius, taken from Rubin et al. (1972). Data for the other galaxies are taken from Smith (1975).

We can also compare the abundance variations among different galaxies with the mass to gas mass ratio. In Fig. 12 we have plotted log [OIII] / H versus log _M / _HI for various locations in a number of galaxies. This plot is more difficult to interpret than Fig. 11. Various assumptions are necessary to convert log [OIII] / H into an abundance ratio and _M / _HI is in the inner parts not equal to _M / _G. Further, we are probably dealing with an atypical sample of galaxies: in both M51 and M101 large scale asymmetries occur which make the determination of _M(r) difficult. If we restrict ourselves to NGC 2403, M33 and M31 we find that, apart from anomalous inner HII regions in M31, a loose correlation exists. The inner parts of M33 and NGC 2403 have about the same linestrength ratio and HI-gas mass to total mass ratio as the outer parts of M31. The mass-to-luminosity ratios in these regions are, however, very different: in the inner parts of M33 and NGC 2403 _M / _LB 3, and in the outer parts (10-20 kpc) of M31 it is about 18. In the outer parts of M31 the abundance of oxygen is about 6 times higher than in the outer parts of M33 (we have used the conversion plot for log [OIII] / H [O/H] given by Sarazin (1976)). Since the ratios of log _M / _HI in these regions differ by only 1.5 we conclude that the yield in the outer parts of M31 must have been higher than in the outer parts of its companion M33. From the comparison of data on our Galaxy, NGC 6822, and the Magellanic Clouds, however, (see Lynden-Bell, 1975, Fig. 1) we find that the, yield must be higher in the dwarf galaxies than in the solar neighbourhood. Apparently there is no simple relation between the yield and a parameter like V_m, which scales with the mass of a galaxy. There is also hardly any correlation between the line strength ratio and morphological type, as can be seen from Fig. 10. Also the results for NGC 6503 and NGC 2403, both Scd III galaxies, obtained by Jensen et al. (1976) show a large difference in line strength ratio. Hence not much can be concluded from these data with regard to the yield in different galaxies.

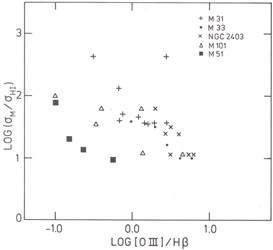Figure 12. Comparison of LOIIIJ/HS ratios and M / HI ratios at various locations in a number of galaxies.

d) Concluding remarks

We have presented the above discussion to illustrate the complexity of the problems we encounter if a simple relation between the abundances of heavy elements and the total mass to gas mass ratio, like equation (1), is to be tested. It is very difficult to draw any conclusions from this discussion other than the obvious one that the uncertainties are large. We find, however, some interesting correlations suggesting a variation of the mass function with radius. No clear relationship exists between the line strength ratio log [OIII] / H and type or size of a galaxy.