Annu. Rev. Astron. Astrophys. 2002. 40: 539-577 Copyright © 2002 by Annual Reviews. All rights reserved

5. COSMOLOGY WITH X-RAY CLUSTERS

5.1. The cosmological mass function

The mass distribution of dark matter halos undergoing spherical collapse in the framework of hierarchical clustering is described by the Press-Schechter distribution (PS, Press &Schechter 1974). The number of such halos in the mass range [M, M + dM] can be written as

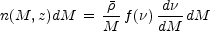(10)

where is the cosmic mean density. The function f depends only on the variable = _c(z) / _M, and is normalized so that f () d = 1. _c(z) is the linear-theory overdensity extrapolated to the present time for a uniform spherical fluctuation collapsing at redshift z. This quantity conveys information about the dynamics of fluctuation evolution in a generic Friedmann background. It is convenient to express it as _c(z) = ₀(z) [D(0) / D(z)], where D(z) is the linear fluctuation growth factor, which depends on the density parameters contributed by matter, _m and by cosmological constant, (e.g. Peebles 1993). The quantity ₀(z) has a weak dependence on _m and (e.g. Kitayama & Suto 1997). For a critical-density Universe it is ₀ = 1.686, independent of z.

The r.m.s. density fluctuation at the mass scale M, _M, is connected to the fluctuation power spectrum, P(k), by the relation

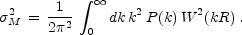(11)

The dependence of the power spectrum on the wavenumber k is usually written as P(k) k^n_pr T²(k), where T(k) is the transfer function, which depends both on the cosmological parameters of the Friedmann background and on the cosmic matter constituents (e.g. fraction of cold, hot and baryonic matter, number of relativistic species; see Kolb & Turner 1989). For a pure cold dark matter (CDM) model, T(k) depends to a good approximation only on the shape parameter = _m h (e.g. Bardeen et al. 1986), while a correction to this dependence needs to be introduced to account for the presence of the baryonic component (e.g. Eisenstein & Hu 1999). The Harrison-Zel'dovich spectrum is generally assumed with the primordial index, n_pr = 1, consistent with the most recent analyses of the CMB anisotropies (de Bernardis et al. 2001 and references therein). The amplitude of P(k) is usually expressed in terms of ₈, the r.m.s. density fluctuation within a top-hat sphere of 8 h^-1 Mpc radius. Finally, in Equation 11 W(x) is the Fourier representation of the window function, which describes the shape of the volume from which the collapsing object is accreting matter. The comoving fluctuation size R is connected to the mass scale M as R = (3M/4 )^1/3 for the top-hat window, i.e. W(x) = 3(sin x - x cos x) / x³.

In their original derivation of the cosmological mass function, Press & Schechter (1974) obtained the expression f () = (2)^-1/2 exp(- ²/2) for Gaussian density fluctuations. Despite its subtle simplicity (e.g., Monaco 1998), the PS mass function has served for more than a decade as a guide to constrain cosmological parameters from the mass function of galaxy clusters. Only with the advent of the last generation of N-body simulations, which are able to span a very large dynamical range, significant deviations of the PS expression from the exact numerical description of gravitational clustering have been noticed (e.g. Gross et al. 1998, Governato et al. 1999, Jenkins et al. 2001, Evrard et al. 2002). Such deviations are interpreted in terms of corrections to the PS approach. For example, incorporating the effects of non-spherical collapse (Sheth et al. 2001) generalizes the above PS expression for f () to

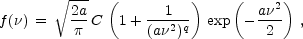(12)

where a = 0.707, C = 0.3222 and q = 0.3 (Sheth & Tormen 1999). The above equation reduces to the PS expression for a = 1, C = 1/2 and q = 0. Fitting formulae for f (), which reproduce N-body results to an accuracy of about 10% (e.g. Evrard et al. 2002) are now currently used to derive cosmological constraints from the evolution of the cluster population.

In practical applications, the observational mass function of clusters is usually determined over about one decade in mass. Therefore, it probes the power spectrum over a relatively narrow dynamical range, and does not provide strong constraints on the shape of the power spectrum. Using only the number density of nearby clusters of a given mass M, one can constrain the amplitude of the density perturbation at the physical scale R (M / _{m crit})^1/3 containing this mass. Since such a scale depends both on M and on _m, the mass function of nearby (z 0.1) clusters is only able to constrain a relation between ₈ and _m. In the left panel of Figure 12 we show that, for a fixed value of the observed cluster mass function, the implied value of ₈ from Equation 12 increases as the density parameter decreases.

Figure 12. The sensitivity of the cluster mass function to cosmological models. (Left) The cumulative mass function at z = 0 for M > 5 × 1014h-1 M for three cosmologies, as a function of 8, with shape parameter = 0.2; solid line: m = 1; short-dashed line: m = 0.3, = 0.7; long-dashed line: m = 0.3, = 0. The shaded area indicates the observational uncertainty in the determination of the local cluster space density. (Right Evolution of n( > M, z) for the same cosmologies and the same mass-limit, with 8 = 0.5 for the m = 1 case and 8 = 0.8 for the low-density models.

Determinations of the cluster mass function in the local Universe using a variety of samples and methods indicate that _m = 0.4 - 0.6, where 0.4 - 0.6, almost independent of the presence of a cosmological constant term providing spatial flatness (e.g. Bahcall & Cen 1993, Eke et al. 1996, Girardi et al. 1998, Viana & Liddle 1999, Blanchard et al. 2000, Pierpaoli et al. 2001, Reiprich & Böhringer 2002, Seljak 2002, Viana et al. 2002). It is worth pointing out that formal statistical uncertainties in the determination of ₈ from the different analyses are always far smaller, 5%, than the above range of values. This suggests that current discrepancies on ₈ are likely to be ascribed to systematic effects, such as sample selection and different methods used to infer cluster masses. We comment more on such differences in the following section. Completely independent constraints on a similar combination of ₈ and _m can be obtained with measurements of the cosmic gravitational lensing shear (e.g. Mellier 1999). The most recent results give _m^0.6 = 0.45 ± 0.05 (van Waerbecke et al. 2001, and references therein).

The growth rate of the density perturbations depends primarily on _m and, to a lesser extent, on , at least out to z ~ 1, where the evolution of the cluster population is currently studied. Therefore, following the evolution of the cluster space density over a large redshift baseline, one can break the degeneracy between ₈ and _m. This is shown in a pictorial way in Figure 1 and quantified in the right panel of Figure 12: models with different values of _m, which are normalized to yield the same number density of nearby clusters, predict cumulative mass functions that progressively differ by up to orders of magnitude at increasing redshifts.