Annu. Rev. Astron. Astrophys. 2002. 40: 539-577 Copyright © 2002 by Annual Reviews. All rights reserved

5.2. Deriving _m from cluster evolution

An estimate of the cluster mass function is reduced to the measurement of masses for a sample of clusters, stretching over a large redshift range, for which the survey volume is well known.

Velocity dispersions for statistical samples of galaxy clusters have been provided by the ESO Nearby Abell Cluster Survey (ENACS; Mazure et al. 2001) and, more recently, by the 2dF survey (de Propris et al. 2002). Application of this method to a statistically complete sample of distant X-ray selected clusters has been pursued by the CNOC (Canadian Network for Observational Cosmology) collaboration (e.g. Yee et al. 1996). The CNOC sample includes 16 clusters from the EMSS in the redshift range 0.17 z 0.55. Approximately 100 redshifts of member galaxies were measured for each cluster, thus allowing an accurate analysis of the internal cluster dynamics (Carlberg et al. 1997b). The CNOC sample has been used to constrain _m through the M / L_opt method (e.g. Carlberg et al. 1997b), yielding _m 0.2 ± 0.05. Attempts to estimate the cluster mass function n( > M) using the cumulative velocity dispersion distribution, n( > _v), were made (Carlberg et al. 1997b). This method, however, provided only weak constraints on _m owing to to the narrow redshift range and the limited number of clusters in the CNOC sample (Borgani et al. 1999, Bahcall et al. 1997). The extension of such methodology to a larger and more distant cluster sample would be extremely demanding from the observational point of view, which explains why it has not been pursued thus far.

A conceptually similar, but observationally quite different method to estimate cluster masses, is based on the measurement of the temperature of the intra-cluster gas (see Section 2). Based on the assumption that gas and dark matter particles share the same dynamics within the cluster potential well, the temperature T and the velocity dispersion _v are connected by the relation k_BT = µ m_{p v}², where = 1 would correspond to the case of a perfectly thermalized gas. If we assume spherical symmetry, hydrostatic equilibrium and isothermality of the gas, the solution of Equation 5 provides the link between the total cluster virial mass, M_vir, and the ICM temperature:

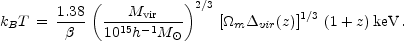(13)

_vir(z) is the ratio between the average density within the virial radius and the mean cosmic density at redshift z (_vir = 18² 178 for _m = 1; see Eke et al. 1996 for more general cosmologies). Equation 13 is fairly consistent with hydrodynamical cluster simulations with 0.9 1.3 (e.g. Bryan & Norman 1998, Frenk et al. 2000; see however Voit 2000). Such simulations have also demonstrated that cluster masses can be recovered from gas temperature with a ~ 20% precision (e.g. Evrard et al. 1996).

Observational data on the M_vir-T relation show consistency with the T M_vir^2/3 scaling law, at least for T 3 keV clusters (e.g. Allen et al. 2001), but with a ~ 40% lower normalization. As for lower-temperature systems, Finoguenov et al. (2001) found some evidence for a steeper slope. Such differences might be due to a lack of physical processes in simulations. For example, energy feedback from supernovae or AGNs and radiative cooling (see Section 2, above) can modify the thermodynamical state of the ICM and the resulting scaling relations.

Measurements of cluster temperatures for flux-limited samples of clusters were made using modified versions of the Piccinotti et al. sample (e.g. Henry & Arnaud 1991). These results have been subsequently refined and extended to larger samples with the advent of ROSAT, Beppo-SAX and, especially, ASCA. With these data one can derive the X-ray Temperature Function (XTF), which is defined analogously to Equation 7. XTFs have been computed for both nearby (e.g. Markevitch 1998, see Pierpaoli et al. 2001, for a recent review) and distant (e.g. Eke et al. 1998, Donahue & Voit 1999, Henry 2000) clusters, and used to constrain cosmological models. The mild evolution of the XTF has been interpreted as a case for a low-density Universe, with 0.2 _m 0.6 (see Figure 13). The starting point in the computation of the XTF is inevitably a flux-limited sample for which (L_X) can be computed. Then the L_X - T_X relation is used to derive a temperature limit from the sample flux limit (e.g. Eke et al. 1998). A limitation of the XTFs presented so far is the limited sample size (with only a few z 0.5 measurements), as well as the lack of a homogeneous sample selection for local and distant clusters. By combining samples with different selection criteria one runs the risk of altering the inferred evolutionary pattern of the cluster population. This can give results consistent even with a critical-density Universe (Colafrancesco et al. 1997, Viana & Liddle 1999, Blanchard et al. 2000).

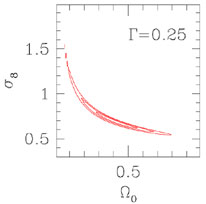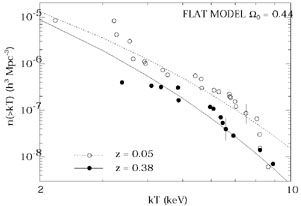
Figure 13. (Left) The cumulative X-ray temperature function for the nearby cluster sample by Henry & Arnaud (1991) and for a sample of moderately distant clusters (from Henry 2000). (Right) Probability contours in the 8 - m plane from the evolution of the X-ray temperature function (adapted from Eke et al. 1998).

Another method to trace the evolution of the cluster number density is based on the XLF. The advantage of using X-ray luminosity as a tracer of the mass is that L_X is measured for a much larger number of clusters within samples well-defined selection properties. As discussed in Section 3, the most recent flux-limited cluster samples contain now a large (~ 100) number of objects, which are homogeneously identified over a broad redshift baseline, out to z 1.3. This allows nearby and distant clusters to be compared within the same sample, i.e. with a single selection function. The potential disadvantage of this method is that it relies on the relation between L_X and M_vir, which is based on additional physical assumptions and hence is more uncertain than the M_vir - _v or the M_vir-T relations.

A useful parameterization for the relation between temperature and bolometric luminosity is

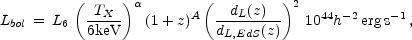(14)

with d_L(z) the luminosity-distance at redshift z for a given cosmology. Several independent analyses of nearby clusters with T_X 2 keV consistently show that L₆ 3 is a stable result and 2.5-3 (e.g. White et al. 1997, Wu et al. 1999, and references therein). For cooler groups, 1 keV, the L_bol - T_X relation steepens, with a slope ~ 5 (e.g. Helsdon & Ponman 2000).

The redshift evolution of the L_X - T relation was first studied by Mushotzky & Scharf (1997) who found that data out to z 0.4 are consistent with no evolution for an Einstein-de-Sitter model (i.e., A 0). This result was extended to higher redshifts using cluster temperatures out to z 0.8 as measured with ASCA and Beppo-SAX data (Donahue et al. 1999, Della Ceca et al. 2000, Henry 2000). The lack of a significant evolution seems to hold beyond z = 1 according to recent Chandra observations of very distant clusters (Borgani et. al. 2001b, Stanford et al. 2001, Holden et al. 2002), as well as Newton-XMM observations in the Lockman Hole (Hashimoto et al. 2002). Figure 14 shows a summary of the observational results on the L_X - T. The high redshift points generally lie around the local relation, thus demonstrating that it is reasonable to assume A 1 implying at most a mild positive evolution of the L_bol - T_X relation. Besides the relevance for the evolution of the mass-luminosity relation, these results also have profound implications for the physics of the ICM (see Section 2).

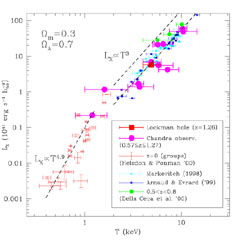Figure 14. The (bolometric) luminosity-temperature relation for nearby and distant clusters and groups compiled from several sources (see Borgani et al. 2001b, Holden et al. 2002). The two dashed lines at T > 2 keV indicate the slope = 3, with normalization corresponding to the local LX - T relation (lower line) and to the relation of Equation 14 computed at z = 1 for A = 1. The dashed line at T < 1 keV shows the best-fitting relation found for groups by Helsdon & Ponman (2000).

Kitayama & Suto (1997) and Mathiesen & Evrard (1998) analyzed the number counts from different X-ray flux-limited cluster surveys (Figure 7) and found that resulting constraints on _m are rather sensitive to the evolution of the mass-luminosity relation. Sadat et al. (1998) and Reichart et al. (1999) analyzed the EMSS and found results to be consistent with _m = 1. Borgani et al. (2001b) analyzed the RDCS sample to quantify the systematics in the determination of cosmological parameters induced by the uncertainty in the mass-luminosity relation (Borgani et al. 1998). They found 0.1 _m 0.6 at the 3 confidence level, by allowing the M - L_X relation to change within both the observational and the theoretical uncertainties. In Figure 15 we show the effect of changing in different ways the parameters defining the M - L_X relation, such as the slope and the evolution A of the L_X - T relation (see Equation 14), the normalization of the M-T relation (see Equation 13), and the overall scatter _M-LX. We assume flat geometry here, i.e. _m + = 1. In general, constraints of cosmological models based on cluster abundance are not very sensitive to (see Figure 12). To a first approximation, the best fit _m has a slight dependence on for open geometry: _{m m,fl} + 0.1(1 - _m,fl - ), where _m,fl is the best fit value for flat geometry.

Constraints on _m from the evolution of the cluster population, like those shown in Figures 13 and 15, are in line with the completely independent constraints derived from the baryon fraction in clusters, f_bar, which can be measured with X-ray observations. If the baryon density parameter, _bar, is known from independent considerations (e.g. by combining the observed deuterium abundance in high-redshift absorption systems with predictions from primordial nucleosynthesis), then the cosmic density parameter can be estimated as _m = _bar / f_bar (e.g. White et al. 1993b). For a value of the Hubble parameter h 0.7, this method yields f_bar 0.15 (e.g. Evrard 1997; Ettori 2001). Values of f_bar in this range are consistent with _m = 0.3 for the currently most favored values of the baryon density parameter, _bar 0.02 h^-2, as implied by primordial nucleosynthesis (e.g. Burles & Tytler 1998) and by the spectrum of CMB anisotropies (e.g. de Bernardis et al. 2001, Stompor et al. 2001, Pryke et al. 2002).

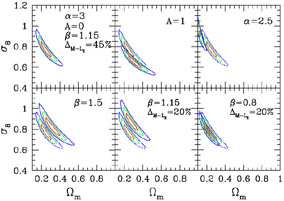Figure 15. Probability contours in the 8-m plane from the evolution of the X-ray luminosity distribution of RDCS clusters. The shape of the power spectrum is fixed to = 0.2. Different panels refer to different ways of changing the relation between cluster virial mass, M, and X-ray luminosity, LX, within theoretical and observational uncertainties (see also Borgani et al. 2001b). The upper left panel shows the analysis corresponding to the choice of a reference parameter set. In each panel, we indicate the parameters which are varied, with the dotted contours always showing the reference analysis.

Figure 15 demonstrates that firm conclusions about the value of the matter density parameter _m can be drawn from available samples of X-ray clusters. In keeping with most of the analyses in the literature, based on independent methods, a critical density model cannot be reconciled with data. Specifically, _m < 0.5 at 3 level even within the full range of current uncertainties in the relation between mass and X-ray luminosity.

A more delicate issue is whether one can use the evolution of galaxy clusters for high-precision cosmology, e.g., 10% accuracy. Serendipitous searches of distant clusters from XMM and Chandra data will eventually lead to a significant increase of the number of high- z clusters with measured temperatures. Thus, the main limitation will lie in systematics involved in comparing the mass inferred from observations with that given by theoretical models. A point of concern, for example, is that constraints on ₈ from different analyses of the cluster abundance differ by up to 30% from each other. While a number of previous studies found ₈ 0.9-1 for _m = 0.3 (e.g. Pierpaoli et al. 2001 and references therein), the most recent analyses point toward a low power spectrum normalization, ₈ 0.7 for _m = 0.3 (Borgani et al. 2001b, Reiprich & Böhringer 2002, Seljak 2002, Viana et al. 2002).

A thorough discussion of the reasons for such differences would require an extensive and fairly technical review of the analysis methods applied so far. For instance, a delicate point concerns the different recipes adopted for the mass-temperature and mass-luminosity conversions. The M-T relation, usually measured at some fixed overdensity from observational data, seems to have a lower normalization than that calibrated from hydrodynamical simulations (e.g. Finoguenov et al. 2001, Allen et al. 2001, Ettori et al. 2002). In turn, this provides a lower amplitude for the mass function implied by an observed XTF and, therefore, a smaller ₈. Several uncertainties also affect the L_X - T relation. The derived slope depends on the temperature range over which the fit is performed. We are also far from understanding the nature of its scatter, i.e. how much it is due to systematics, and how much it is intrinsic, inherent to complex physical conditions in the gas. For example, the contribution of cooling flows is known to increase the scatter in the L_X - T relation (e.g. Markevitch 1998, Allen & Fabian 1998, Arnaud & Evrard 1999). Adding such a scatter in the mass-luminosity conversion increases the amplitude of the mass-function, especially in the high-mass tail, thus decreasing the required ₈.

As an illustrative example, we show in Figure 15 how constraints in the ₈-_m plane move as we change the scatter and the amplitude of the M-L_X relation in the analysis of the RDCS. The upper left panel shows the result for the same choice of parameters as in the original analysis by Borgani et al. (2001b), which gives ₈ 0.7 for _m = 0.3. The central lower panel shows the effect of decreasing the scatter of the M-L_X relation by 20%, in keeping with the analysis by Reiprich & Böhringer (2002, see also Ettori et al. 2002). Such a reduced scatter causes ₈ to increase by about 20%. Finally, if the normalization of the M-T relation is decreased by ~ 30% with respect to the value suggested by hydrodynamical cluster simulations (lower right panel), ₈ is again decreased by ~ 20%.

In light of this discussion, a 10% precision in the determination of fundamental cosmological parameters, such as _m and ₈ lies in the future. With forthcoming datasets the challenge will be in comparing observed clusters with the theoretical clusters predicted by Press-Schechter-like analytical approaches or generated by numerical simulations of cosmic structure formation.