7. NEUTRINOS

7.1. The decaying-neutrino hypothesis

Experiments now indicate that neutrinos possess nonzero rest mass and make up at least part of the dark matter (Sec. 4.4). If different neutrino species have different rest masses, then heavier ones can decay into lighter ones plus a photon. These decay photons might be observable, as first appreciated by Cowsik in 1977 [238] and de Rujula and Glashow in 1980 [239]. The strength of the expected signal depends on the way in which neutrino masses are incorporated into the standard model of particle physics. In minimal extensions of this model, radiative neutrino decays are characterized by lifetimes on the order of 10²⁹ yr or more [240]. This is so much longer than the age of the Universe that neutrinos are effectively stable, and would not produce a detectable signal. In other theories, however, such as those involving supersymmetry, their decay lifetime can drop to as low as 10¹⁵ yr [241]. This is within five orders of magnitude of the age of the Universe and opens up the possibility of significant contributions to the background light.

Decay photons from neutrinos with lifetimes this short are also interesting for another reason: their existence might resolve a number of longstanding astrophysical puzzles involving the ionization of hydrogen and nitrogen in the interstellar and intergalactic medium [242, 243]. As first pointed out by Melott in 1988 [244], these would be particularly well explained by neutrinos decaying on timescales of order ~ 10²⁴ s with rest energies m ~ 30 eV. This latter value fits awkwardly with current thinking on large-scale structure formation in the early Universe (Sec. 4.4). Neutrinos of this kind could help with so many other problems, however, that they have continued to draw the interest of cosmologists. Sciama and his colleagues, in particular, were led on this basis to develop a detailed scenario known as the decaying-neutrino hypothesis [93, 245, 246], in which the rest energy and decay lifetime of the massive -neutrino are given respectively by

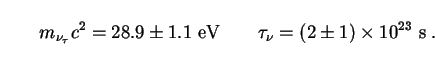(191)

The neutrino decays into a µ neutrino plus a photon (Fig. 28). Assuming that m >> m_µ, conservation of energy and momentum require this photon to have an energy E = 1/2 m c² = 14.4 ± 0.5 eV. The concreteness of this proposal has made it eminently testable. Some of the strongest bounds come from searches for line emission near 14 eV that would be expected from concentrations of decaying dark matter in clusters of galaxies. No such signal has been seen in the direction of the galaxy cluster surrounding the quasar 3C 263 [247], or in the direction of the rich cluster Abell 665 which was observed using the Hopkins Ultraviolet Telescope in 1991 [248]. It may be, however, that absorption plays a stronger role than expected along the lines of sight to these clusters, or that most of their dark matter is in another form [241, 249]. A potentially more robust test of the decaying-neutrino hypothesis comes from the diffuse background light. This has been looked at in a number of studies [250, 251, 252, 253, 254, 255, 256]. The task is a challenging one for several reasons. Decay photons of energy near 14 eV are strongly absorbed by both dust and neutral hydrogen, and the distribution of these quantities in intergalactic space is uncertain. It is also notoriously difficult, perhaps more so in this part of the spectrum than any other, to distinguish between those parts of the background which are truly extragalactic and those which are due to a complex mixture of competing foreground signals [257, 258]. We reconsider the problem here with the help of the formalism developed in Secs. 2 and 3, adapting it to allow for absorption by gas and dust.

Figure 28. Feynman diagrams corresponding to the decay of a massive neutrino (1) into a second, lighter neutrino species (2) together with a photon (). The process is mediated by charged leptons ( ) and the W boson (W).

7.2. Neutrino halos

To begin with, we take as our sources of background radiation the neutrinos which have become trapped in the gravitational potential wells surrounding individual galaxies. (Not all the neutrinos will be bound in this way; and we will deal with the others separately.) The comoving number density of these galactic neutrino halos is just that of the galaxies themselves: n₀ = 0.010 h₀³ Mpc^-3 from Eq. (172).

The wavelength of the neutrino-decay photons at emission (like those from axion decay in Sec. 6.5) can be taken to be distributed normally about the peak wavelength corresponding to E:

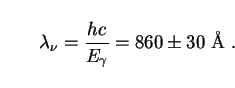(192)

This lies in the extreme ultraviolet (EUV) portion of the spectrum, although the redshifted tail of the observed photon spectrum will stretch across the far ultraviolet (FUV) and near ultraviolet (NUV) bands. (Universal conventions regarding the boundaries between these wavebands have yet to be established. For definiteness, we take them as follows: EUV = 100-912 Å, FUV = 912-2000 Å and NUV = 2000-4000 Å.) The spectral energy distribution (SED) of the neutrino halos is then given by Eq. (75):

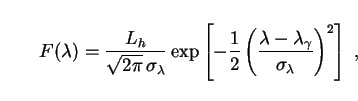(193)

where L_h, the halo luminosity, has yet to be determined. For the standard deviation we can follow the same procedure as with axions and use the velocity dispersion in the halo, giving = 2 v_c / c. We parametrize this for convenience using the range of uncertainty in the value of , so that ₃₀ / (30 Å).

The halo luminosity is just the ratio of the number of decaying neutrinos (N) to their decay lifetime (), multiplied by the energy of each decay photon (E). Because the latter is just above the hydrogen-ionizing energy of 13.6 eV, we also need to multiply the result by an efficiency factor () between zero and one, to reflect the fact that some of the decay photons are absorbed by neutral hydrogen in their host galaxy before they can leave the halo and contribute to its luminosity. Altogether, then:

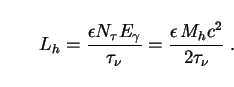(194)

Here we have expressed N as the number of neutrinos with rest mass m = 2E / c² per halo mass M_h.

To calculate the mass of the halo, let us follow reasoning similar to that adopted for axion halos in Sec. 6.3 and assume that the ratio of baryonic to total mass in the halo is comparable to the ratio of baryonic to total matter density in the Universe, (M_tot - M_h) / M_tot = M_bar / M_tot = _bar / (_bar + ). Here we have made also the economical assumption that there are no other contributions to the matter density, apart from those of baryons and massive neutrinos. It the follows that

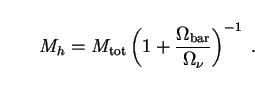(195)

We take M_tot = (2 ± 1) × 10¹² M following Eq. (175). For _bar we use the value (0.016 ± 0.005) h₀^-2 quoted in Sec. 4.2. And to calculate we put the neutrino rest mass m into Eq. (96), giving

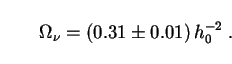(196)

Inserting these values of M_tot, _bar and into (195), we obtain

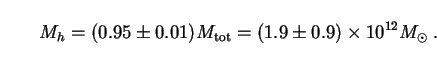(197)

The uncertainty h₀ in Hubble's constant scales out of this result. Eq. (197) implies a baryonic mass M_bar = M_tot - M_h 1 × 10¹¹ M, in good agreement with the observed sum of contributions from disk, bulge and halo stars plus the matter making up the interstellar medium in our own Galaxy.

The neutrino density (196), when combined with that of baryons, leads to a total present-day matter density of

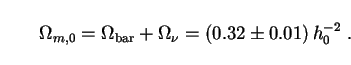(198)

As pointed out by Sciama [93], massive neutrinos are thus consistent with a critical-density Einstein-de Sitter Universe (_m,0 = 1) if

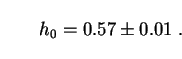(199)

This is just below the range of values which many workers now consider observationally viable for Hubble's constant (Sec. 4.2). But it is a striking fact that the same neutrino rest mass which resolves several unrelated astrophysical problems also implies a reasonable expansion rate in the simplest cosmological model. In the interests of testing the decaying-neutrino hypothesis in a self-consistent way, we will follow Sciama in adopting the narrow range of values (199) for Sec. 7 only.

7.3. Halo luminosity

To evaluate the halo luminosity (194), it remains to find the fraction of decay photons which escape from the halo. The problem is simplified by recognizing that the photo-ionization cross-section and distribution of neutral hydrogen in the Galaxy are such that effectively all of the decay photons striking the disk are absorbed. The probability of absorption for a single decay photon is then proportional to the solid angle subtended by the Galactic disk, as seen from the point where the photon is released.

We model the distribution of neutrinos (and their decay photons) in the halo with a flattened ellipsoidal profile which has been advocated in the context of the decaying-neutrino scenario by Salucci and Sciama [259]. This has

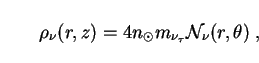(200)

with

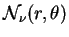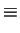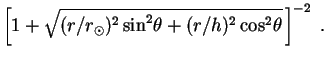Here r and are spherical coordinates, n = 5 × 10⁷ cm^-3 is the local neutrino number density, r = 8 kpc is the distance of the Sun from the Galactic center, and h = 3 kpc is the scale height of the halo. Although this function has essentially been constructed to account for the ionization structure of the Milky Way, it agrees reasonably well with dark-matter halo distributions which have derived on strictly dynamical grounds [260].

Defining x r / r, one can use (200) to express the mass M_h of the halo in terms of a halo radius (r_h) as

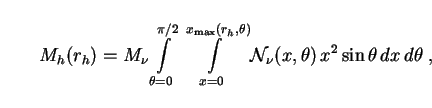(201)

where

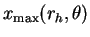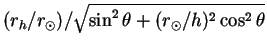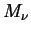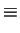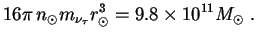Outside x > x_max, we assume that the halo density drops off exponentially and can be ignored. Using (201) it can be shown that halos whose masses M_h are given by (197) have scale radii r_h = (70 ± 25) kpc. This is consistent with evidence from the motion of Galactic satellites [75].

We now put ourselves in the position of a decay photon released at cylindrical coordinates (y, z) inside the halo, Fig. 29(a).

Figure 29. Panel (a): absorption of decay photons inside the halo. For neutrinos decaying at (y, z), the probability that decay photons will be absorbed inside the halo (radius rh) is essentially the same as the probability that they will strike the Galactic disk (radius rd, shaded). Panel (b): an ellipse of semi-major axis a, semi-minor axis b and radial arm r() subtends angles of , and () respectively.

It may be seen that the disk of the Galaxy presents an approximately elliptical figure with maximum angular width 2 and angular height 2, where

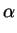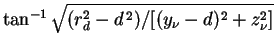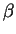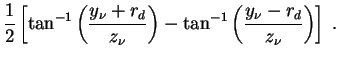			(202)

Here r_d is the disk radius, d = [(y² + z² + r_d²) - [(y² + z² + r_d²)² - 4y² r_d²]^1/2 / 2 y, y = r sin and z = r cos. In spherical coordinates centered on the photon, the solid angle subtended by an ellipse is

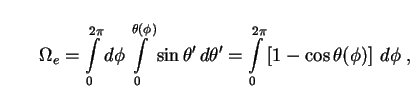(203)

where () is the angle subtended by a radial arm of the ellipse, as shown in Fig. 29(b). The cosine of this angle is expressed in terms of and by

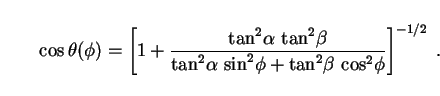(204)

The single-point probability that a photon released at (x,) will escape from the halo is then 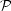_e = 1 - _e(, ) / 4. For a given halo size r_h, we obtain a good approximation to by averaging 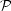_e over all locations (x, ) in the halo and weighting by the neutrino number density . Choosing r_d = 36 kpc as an effective disk radius [1], we obtain:

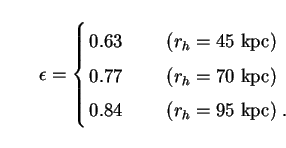(205)

As expected, the escape fraction of decay photons goes up as the scale size of the halo increases relative to that of the disk. As r_h >> r_d one gets 1, while a small halo with r_h r_d leads to 0.5.

With the decay lifetime , halo mass M_h and efficiency factor all known, Eq. (194) gives for the luminosity of the halo:

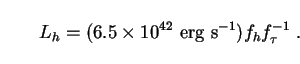(206)

Here we have introduced two dimensionless constants f_h and f in order to parametrize the uncertainties in M_h and . For the ranges of values given above, these take the values f_h = 1.0 ± 0.6 and f = 1.0 ± 0.5 respectively. Setting f_h = f = 1 gives a halo luminosity of about 2 × 10⁹ L, or less than 5% of the optical luminosity of the Milky Way (L₀ = 2 × 10¹⁰ h₀^-2 L), with h₀ as specified by Eq. (199).

The combined bolometric intensity of decay photons from all the bound neutrinos out to a redshift z_f is given by (16) as usual:

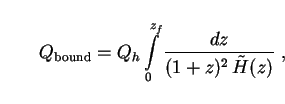(207)

where

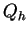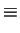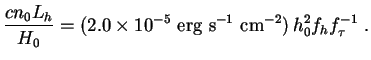The h₀-dependence in this quantity comes from the fact that we have so far considered only neutrinos in galaxy halos, whose number density n₀ goes as h₀³. Since we follow Sciama in adopting the Einstein-de Sitter (EdS) cosmology in this section, the Hubble expansion rate (33) is

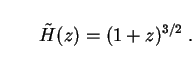(208)

Putting this into (207), we find

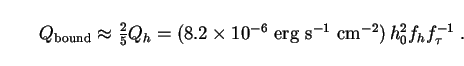(209)

(The approximation is good to better than 1% if z_f 8.) Here we have neglected absorption between the galaxies, an issue we will return to below. Despite their mass and size, dark-matter halos in the decaying-neutrino hypothesis are not very bright. Their combined intensity is about 1% of that of the EBL due to galaxies, Q_* 3 × 10^-4 erg s^-1 cm^-2. This is primarily due to the long decay lifetime of the neutrinos, five orders of magnitude longer than the age of the galaxies.

7.4. Free-streaming neutrinos

The cosmological density of decaying neutrinos in dark-matter halos is small: _,bound = n₀ M_h / _crit = (0.068 ± 0.032)h₀. With h₀ as given by (199), this amounts to less than 6% of the total neutrino density, Eq. (196). Therefore, as expected for hot dark matter particles, the bulk of the EBL contributions in the decaying-neutrino scenario come from neutrinos which are distributed on larger scales. We will refer to these collectively as free-streaming neutrinos, though some of them may actually be associated with more massive systems such as clusters of galaxies. (The distinction is not critical for our purposes, since we are concerned with combined contributions to the diffuse background.) Their cosmological density is found using (196) as _,free = - _,bound = 0.30h₀^-2 f_f, where the dimensionless constant f_f = 1.00 ± 0.05 parametrizes the uncertainties in this quantity.

To identify sources of radiation in this section we follow the same procedure as with vacuum energy (Sec. 5.6) and divide the Universe into regions of comoving volume V₀ = n₀^-1. The mass of each region is

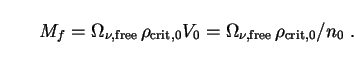(210)

The luminosity of these sources has the same form as Eq. (194) except that we put M_h M_f and drop the efficiency factor since the density of intergalactic hydrogen is too low to absorb a significant fraction of the decay photons within each region. Thus,

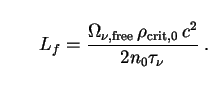(211)

With the above values for _,free and , and with _crit,0 and n₀ given by (24) and (172) respectively, Eq. (211) implies a comoving luminosity density due to free-streaming neutrinos of

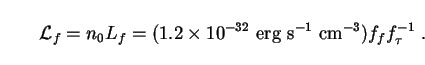(212)

This is 0.5h₀^-1 times the luminosity density of the Universe, as given by Eq. (20). To calculate the bolometric intensity of the background radiation due to free-streaming neutrinos, we replace L_h with L_f in (207), giving

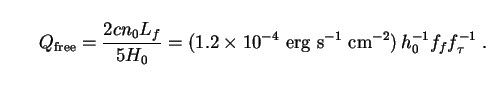(213)

This is of the same order of magnitude as Q_*, and goes as h₀^-1 rather than h₀². Taking into account the uncertainties in h₀, f_h, f_f and f, the bolometric intensity of bound and free-streaming neutrinos together is

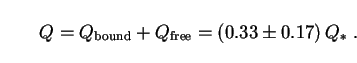(214)

In principle, then, these particles are capable of shining as brightly as the galaxies themselves, Eq. (41). Most of this light is due to free-streaming neutrinos, which are both more numerous than their halo-bound counterparts and unaffected by absorption at source.

7.5. Extinction by gas and dust

To obtain more quantitative constraints, we would like to determine neutrino contributions to the EBL as a function of wavelength. This is accomplished as in previous sections by putting the source luminosity (L_h for the galaxy halos or L_f for the free-streaming neutrinos) into the SED (193), and substituting the latter into Eq. (62). Now, however, we also wish to take into account the fact that decay photons encounter significant amounts of absorbing material as they travel through the intergalactic medium. The wavelength of neutrino decay photons, = 860 ± 30 Å, is just shortward of the Lyman- line at 912 Å, which means that these photons are absorbed almost as strongly as they can be by neutral hydrogen (this, of course, is one of the prime motivations of the theory). It is also very close to the waveband of peak extinction by dust. The simplest way to handle both these types of absorption is to include an opacity term (₀, z) inside the argument of the exponential, so that intensity reads

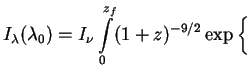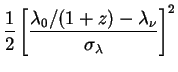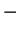			(215)

Here we have used (208) for 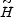(z). The prefactor I is given with the help of (206) for bound neutrinos and (211) for free-streaming ones as

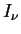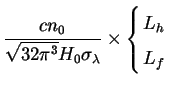			(216)

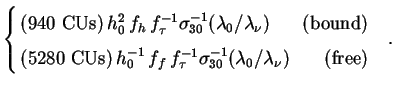The optical depth (₀, z) can be broken into separate terms corresponding to hydrogen gas and dust along the line of sight:

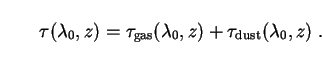(217)

Our best information about both of these quantities comes from observations of quasars at high redshifts. The fact that these are visible at all already places a limit on the degree of attenuation in the intergalactic medium.

We begin with the gas component. Zuo and Phinney [261] have developed a formalism to describe the absorption due to randomly distributed clouds such as quasar absorption-line systems and normalized this to the number of Lyman-limit systems at z = 3. We use their model 1, which gives the highest absorption below ₀ 2000 Å, making it conservative for our purposes. Assuming an EdS cosmology, the optical depth at ₀ due to neutral hydrogen out to a redshift z is given by

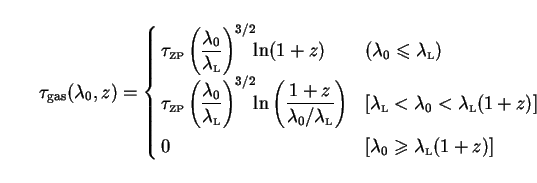(218)

where _L = 912 Å and _ZP = 2.0.

Dust is a more complicated and potentially more important issue, and we pause to discuss this critically before proceeding. The simplest possibility, and the one which should be most effective in obscuring a diffuse signal like that considered here, would be for dust to be spread uniformly through intergalactic space. A quantitative estimate of opacity due to a uniform dusty intergalactic medium has in fact been suggested [262], but is regarded as an extreme upper limit because it would lead to excessive reddening of quasar spectra [263]. Subsequent discussions have tended to treat intergalactic dust as clumpy [264], with significant debate about the extent to which such clumps would redden and/or hide background quasars, possibly helping to explain the observed "turnoff" in quasar population at around z ~ 3 [265, 266, 267, 268]. Most of these models assume an EdS cosmology. The effects of dust extinction could be enhanced if _m,0 < 1 and/or _,0 > 0 [267], but we ignore this possibility here because neutrinos (not vacuum energy) are assumed to make up the critical density in the decaying-neutrino scenario.

We will use a formalism due to Fall and Pei [269] in which dust is associated with damped Ly absorbers whose numbers and density profiles are sufficient to obscure a portion of the light reaching us from z ~ 3, but not to account fully for the turnoff in quasar population. Obscuration is calculated based on the column density of hydrogen in these systems, together with estimates of the dust-to-gas ratio, and is normalized to the observed quasar luminosity function. The resulting mean optical depth at ₀ out to redshift z is

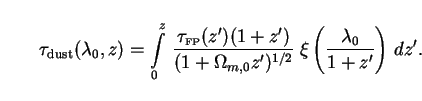(219)

Here () is the extinction of light by dust at wavelength relative to that in the B-band (4400 Å). If _FP(z) = constant and () ^-1, then _dust is proportional to ₀^-1[(1 + z)³ - 1] or ₀^-1[(1 + z)^2.5 - 1], depending on cosmology [262, 264]. In the more general treatment of Fall and Pei [269], _FP(z) is parametrized as a function of redshift so that

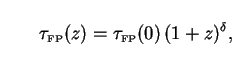(220)

where _FP(0) and are adjustable parameters. Assuming an EdS cosmology (_m,0 = 1), the observational data are consistent with lower limits of _*(0) = 0.005, = 0.275 (model A); best-fit values of _*(0) = 0.016, = 1.240 (model B); or upper limits of _*(0) = 0.050, = 2.063 (model C). We will use all three models in what follows.

The shape of the extinction curve () in the 300-2000 Å range can be computed using numerical Mie scattering routines in conjunction with various dust populations. Many people have constructed dust-grain models that reproduce the average extinction curve for the diffuse interstellar medium (DISM) at > 912 Å [270], but there have been fewer studies at shorter wavelengths. One such study was carried out by Martin and Rouleau [271], who extended earlier calculations of Draine and Lee [272] assuming: (1) two populations of homogeneous spherical dust grains composed of graphite and silicates respectively; (2) a power-law size distribution of the form a^-3.5 where a is the grain radius; (3) a range of grain radii from 50-2500 Å; and (4) solar abundances of carbon and silicon [273].

The last of these assumptions is questionable in light of recent work suggesting that heavy elements are less abundant in the DISM than they are in the Sun. Snow and Witt [274] report interstellar abundances of 214 × 10^-6/H and 18.6 × 10^-6/H for carbon and silicon respectively (relative to hydrogen). This reduces earlier values by half and actually makes it difficult for a simple silicate/graphite model to reproduce the observed DISM extinction curve. We therefore use new dust-extinction curves based on the revised abundances. In the interests of obtaining conservative bounds on the decaying-neutrino hypothesis, we also consider four different grain populations, looking in particular for those that provide optimal extinction efficiency in the FUV without drifting too far from the average DISM curve in the optical and NUV bands. We describe the general characteristics of these models below and show the resulting extinction curves in Fig. 30; details can be found in [256].

Figure 30. The FUV extinction (relative to that in the B-band) produced by five different dust-grain populations. Standard grains (population 1) produce the least extinction, while PAH-like carbon nanoparticles (population 3) produce the most extinction near the neutrino-decay line at 860 Å (vertical line).

Our population 1 grain model (Fig. 30, dash-dotted line) assumes the standard grain model employed by other workers, but uses the new, lower abundance numbers together with dielectric functions due to Draine [275]. The shape of the extinction curve provides a reasonable fit to observation at longer wavelengths (reproducing for example the absorption bump at 2175 Å); but its magnitude is too low, confirming the inadequacies of the old dust model. Extinction in the vicinity of the neutrino-decay line at 860 Å is also weak, so that this model is able to "hide" very little of the light from decaying neutrinos. Insofar as it almost certainly underestimates the true extent of extinction by dust, this grain model provides a good lower limit on absorption in the context of the decaying-neutrino hypothesis.

The silicate component of our population 2 grain model (Fig. 30, short-dashed line) is modified along the lines of the "fluffy silicate" model which has been suggested as a resolution of the heavy-element abundance crisis in the DISM [276]. We replace the standard silicates of population 1 by silicate grains with a 45% void fraction, assuming a silicon abundance of 32.5 × 10^-6 / H [256]. We also decrease the size of the graphite grains (a = 50 - 250 Å) and reduce the carbon depletion to 60% to better match the DISM curve. This mixture provides a better match to the interstellar data at optical wavelengths, and also shows significantly more FUV extinction than population 1.

For population 3 (Fig. 30, dotted line), we retain the standard silicates of population 1 but modify the graphite component as an approximation to the polycyclic aromatic hydrocarbon (PAH) nanostructures which have been proposed as carriers of the 2175 Å absorption bump [277]. PAH nanostructures consist of stacks of molecules such as coronene (C₂₄H₁₂), circumcoronene (C₅₄H₁₈) and larger species in various states of edge hydrogenation. They have been linked to the 3.4 µm absorption feature in the DISM [278] as well as the extended red emission in nebular environments [279]. With sizes in the range 7 - 30 Å, these structures are much smaller than the canonical graphite grains. Their dielectric functions, however, go over to that of graphite in the high-frequency limit [277]. So as an approximation to these particles, we use spherical graphite grains with extremely small radii (3 - 150 Å). This greatly increases extinction near the neutrino-decay peak.

Our population 4 grain model (Fig. 30, long-dashed line) combines both features of populations 2 and 3. It has the same fluffy silicate component as population 2, and the same graphite component as population 3. The results are not too different from those obtained with population 3, because extinction in the FUV waveband is dominated by small-particle contributions, so that silicates (whatever their void fraction) are of secondary importance. Neither the population 3 nor the population 4 grains fit the average DISM curve as well as those of population 2, because the Mie scattering formalism cannot accurately reproduce the behaviour of nanoparticles near the 2175 Å resonance. However, the high levels of FUV extinction in these models -- especially model 3 near 860 Å -- suit them well for our purpose, which is to set the most conservative possible limits on the decaying-neutrino hypothesis.

7.6. The ultraviolet background

We are now ready to specify the total optical depth (217) and hence to evaluate the intensity integral (215). We will use three combinations of the dust models just described, with a view to establishing lower and upper bounds on the EBL intensity predicted by the theory. A minimum-absorption model is obtained by combining Fall and Pei's model A with the extinction curve of the population 1 (standard) dust grains. At the other end of the spectrum, model C of Fall and Pei together with the population 3 (nanoparticle) grains provides the most conservative maximum-absorption model (for ₀ 800 Å). Finally, as an intermediate model, we combine model B of Fall and Pei with the extinction curve labelled as population 0 in Fig. 30.

The resulting predictions for the spectral intensity of the FUV background due to decaying neutrinos are plotted in Fig. 31 (light lines) and compared with observational limits (heavy lines and points). The curves in the bottom half of this figure refer to EBL contributions from bound neutrinos only, while those in the top half correspond to contributions from both bound and free-streaming neutrinos together.

Figure 31. The spectral intensity I of background radiation from decaying neutrinos as a function of observed wavelength 0 (light curves), plotted together with observational upper limits on EBL intensity in the far ultraviolet (points and heavy curves). The bottom four theoretical curves refer to bound neutrinos only, while the top four refer to bound and free-streaming neutrinos together. The minimum predicted signals consistent with the theory are combined with the highest possible extinction in the intergalactic medium, and vice versa.

They are best compared with an experimental measurement by Martin and Bowyer in 1989 [280], labelled "MB89" in Fig. 31. These authors used data from a rocket-borne imaging camera to search for small-scale fluctuations in the FUV EBL, and deduced from this that the combined light of external galaxies (and their associated halos) reaches the Milky Way with an intensity of 16-52 CUs over 1350-1900 Å. There is now some doubt as to whether this was really an extragalactic signal, and indeed whether it is feasible to detect such a signal at all, given the brightness and fluctuations of the Galactic foreground in this waveband [281]. Viable or not, however, it is of interest to see what a detection of this order would mean for the decaying-neutrino hypothesis. Fig. 31 shows that it would constrain the theory only weakly. The expected signal in this waveband lies below 20 CUs in even the most optimistic scenario where signal strength is highest and absorption is weakest. In the nominal "best-fit" scenario this drops to less than 7 CUs. As noted already (Sec. 7.3), the low intensity of the background light from decaying neutrinos is due to their long decay lifetime. In order to place significant constraints on the theory, one needs the stronger signal which comes from free-streaming, as well as bound neutrinos. This in turn requires limits on the intensity of the total background rather than that associated with fluctuations.

The curves in the upper half of Fig. 31 (with peak intensities of about 300, 700 and 2000 CUs at ₀ 900 Å) represent the combined EBL contributions from all decaying neutrinos. We let f_h and f_f take their minimum, nominal and maximum values respectively in (215), with the reverse order applying to f as well as h₀ (the latter change being due to the fact that the dominant free-streaming contribution goes as h₀^-1 rather than h₀²). Simultaneously we adopt the maximum, intermediate and minimum-absorption models for intergalactic dust, as above. Intensity is reduced very significantly in the maximum-absorption case (solid line): by 11% at 900 Å, 53% at 1400 Å and 86% at 1900 Å. The bulk of this reduction is due to dust, especially at longer wavelengths where most of the light originates at high redshifts. Comparable reduction factors in the intermediate-absorption case (short-dashed line) are 9% at 900 Å, 28% at 1400 Å and 45% at 1900 Å. In the minimum-absorption case (long-dashed line), most of the extinction is due to gas rather than dust at shorter wavelengths, and intensity is reduced by a total of 9% at 900 Å, 21% at 1400 Å and 31% at 1900 Å.

The most conservative constraints on the theory are obtained by comparing the lowest predicted intensities (solid line) with observational upper limits on total EBL intensity in the FUV band (Fig. 31). A word is in order about these limits, which can be usefully divided into two groups: those above and below the Lyman -line at 1216 Å. At the longest wavelengths we include two datapoints from Lillie and Witt's analysis of OAO-2 satellite data ([20], labelled "LW76" in Fig. 31); these were already encountered in Sec. 3. Close to them is an upper limit from the Russian Prognoz satellite by Zvereva ([282]; "Z82"). Considerably stronger broadband limits have come from rocket experiments by Paresce ([283]; "P79"), Anderson ([284]; "A79") and Feldman ([285]; "Fe81"), as well as an analysis of data from the Solrad-11 spacecraft by Weller ([286]; "We83").

A number of other studies have proceeded by establishing a correlation between background intensity and the column density of neutral hydrogen inside the Milky Way, and then extrapolating this out to zero column density to obtain the presumed extragalactic component. Martin [287] applied this correlation method to data taken by the Berkeley UVX experiment, setting an upper limit of 110 CUs on the intensity of any unidentified EBL contributions over 1400-1900 Å ("Ma91"). The correlation method is subject to uncertainties involving the true extent of scattering by dust, as well as absorption by ionized and molecular hydrogen at high Galactic latitudes. Henry [258] and Henry and Murthy [289] approach these issues differently and raise the upper limit on background intensity to 400 CUs over 1216-3200 Å. A good indication of the complexity of the problem is found at 1500 Å, where Fix [290] used data from the DE-1 satellite to identify an isotropic background flux of 530 ± 80 CUs ("Fi89"), the highest value reported so far. The same data were subsequently reanalyzed by Wright [288] who found a much lower best-fit value of 45 CUs, with a conservative upper limit of 500 CUs ("Wr92"). The former would rule out the decaying-neutrino hypothesis, while the latter does not constrain it at all. A third treatment of the same data has led to an intermediate result of 300 ± 80 CUs ([291]; "WP94").

Limits on the FUV background shortward of Ly have been even more controversial. Several studies have been based on data from the Voyager 2 ultraviolet spectrograph, beginning with that of Holberg [292], who obtained limits between 100 and 200 CUs over 500-1100 Å (labelled "H86" in Fig. 31). An analysis of the same data over 912-1100 Å by Murthy [293] led to similar numbers. In a subsequent reanalysis, however, Murthy [294 tightened this bound to 30 CUs over the same waveband ("Mu99"). The statistical validity of these results has been debated vigorously [295, 296], with a second group asserting that the original data do not justify a limit smaller than 570 CUs ("E00"). Of these Voyager-based limits, the strongest ("Mu99") is incompatible with the decaying-neutrino hypothesis, while the weakest ("E00") constrains it only mildly. Two new experiments have yielded results midway between these extremes: the DUVE orbital spectrometer [297] and the EURD spectrograph aboard the Spanish MINISAT 01 [298]. Upper limits on continuum emission from the former instrument are 310 CUs over 980-1020 Å and 440 CUs over 1030-1060 Å ("K98"), while the latter has produced upper bounds of 280 CUs at 920 Å and 450 CUs at 1000 Å ("E01").

What do these observational data imply for the decaying-neutrino hypothesis? Longward of Ly, Fig. 31 shows that they span very nearly the same parameter space as the minimum and maximum-intensity predictions of the theory (solid and long-dashed lines). Most stringent are Weller's Solrad-11 result ("We83") and the correlation-method constraint of Martin ("Ma91"). Taken on their own, these data constrain the decaying-neutrino hypothesis rather severely, but do not rule it out. Absorption (by dust in particular) plays a critical role in reducing the strength of the signal.

Shortward of Ly, most of the signal originates nearby and intergalactic absorption is far less important. Ambiguity here comes rather from the spread in reported limits, which in turn reflects the formidable experimental challenges in this part of the spectrum. Nevertheless it is clear that both the Voyager-based limits of Holberg ("H86") and Murthy ("Mu99"), as well as the new EURD measurement at 920 Å ("E01") are incompatible with the theory. These upper bounds are violated by even the weakest predicted signal, which assumes the strongest possible extinction (solid line). The easiest way to reconcile theory with observation is to increase the neutrino decay lifetime. If we require that I_th < I_obs, then the abovementioned EURD measurement ("E01") implies a lower bound of > 3 × 10²³ s. This rises to (5 ± 3) × 10²³ s and (26 ± 10) × 10²³ s for the Voyager limits ("H86" and "Mu99" respectively). All these numbers lie outside the range of lifetimes required in the decaying-neutrino scenario, = (2 ± 1) × 10²³ s. The DUVE constraint ("K98") is more forgiving but still pushes the theory to the edge of its available parameter space. Taken together, these data may safely be said to exclude the decaying-neutrino hypothesis. This conclusion is in accord with current thinking on the value of Hubble's constant (Sec. 4.2) and structure formation (Sec. 4.4), as well as more detailed analysis of the EURD data [299].

These limits would be weakened (by a factor of up to nearly one-third) if the value of Hubble's constant h₀ were allowed to exceed 0.57 ± 0.01, since the dominant free-streaming contributions to I(₀) go as h₀^-1. A higher expansion rate would however exacerbate problems with structure formation and the age of the Universe, the more so because the dark matter in this theory is hot. It would also mean sacrificing the critical density of neutrinos. Another possibility would be to consider lower neutrino rest masses, a scenario that does not conflict with other observational data until m c² 2 eV [300]. This would however entail a proportional reduction in decay photon energy, which would have to drop below the Lyman or hydrogen-ionizing limit, thus removing the whole motivation for the proposed neutrinos in the first place. Similar considerations apply to neutrinos with longer decay lifetimes.

Our conclusions, then, are as follows. Neutrinos with rest masses and decay lifetimes as specified by the decaying-neutrino scenario produce levels of ultraviolet background radiation very close to, and in some cases above experimental upper limits on the intensity of the EBL. At wavelengths longer than 1200 Å, where intergalactic absorption is most effective, the theory is marginally compatible with observation -- if one adopts the upper limits on dust density consistent with quasar obscuration, and if the dust grains are extremely small. At wavelengths in the range 900-1200 Å, predicted intensities are either comparable to or higher than those actually seen. Thus, while there is now good experimental evidence that some of the dark matter is provided by massive neutrinos, the light of the night sky tells us that these particles cannot have the rest masses and decay lifetimes attributed to them in the decaying-neutrino hypothesis.