


How do we compare the dark energy "reach" of different methods and different experiments? We cannot quantify the probative power of dark energy methods in a strictly model-independent way, since we do not know which aspects of the expansion history are most important to measure. Nevertheless, some useful figures of merit (FoMs) have been proposed to facilitate comparison of methods and experimental designs. Examples include the volume of the uncertainty ellipsoid for the dark energy parameters or the thickness of the ellipsoid in its narrowest direction [Huterer & Turner 2001]. In the Fisher matrix approach (Section 11.2), these correspond to the inverse square root of the determinant and the largest eigenvalue of the Fisher matrix, respectively. A special case of the volume FoM is the inverse area of the Fisher-matrix-projected ellipse in the w0 - wa plane,
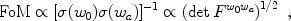 |
(37) |
where Fw0 wa is the Fisher matrix projected onto the w0 - wa plane. This choice was adopted by the Dark Energy Task Force as a metric for comparing methods and surveys and is shown in relative terms for Stage IV space-based experiments in Fig. 16. The DETF FoM provides a simple yet useful metric for comparison, as it takes into account the power of experiments to measure the temporal variation of w. For generalizations, see [Albrecht & Bernstein 2007].
11.2. Fisher information matrix
The Fisher information matrix formalism allows a quick and easy way to
estimate errors on cosmological parameters, given errors in observable
quantities, and is particularly useful in experimental design. The
Fisher matrix is defined as the (negative) Hessian of the log-likelihood
function  ,
,
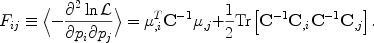 |
(38) |
The second equality follows by assuming that
 is Gaussian in the
observables; here
µ is the vector of mean values of the observables,
C is their covariance matrix, and ,i
denotes a derivative with respect to ith model parameter
pi. The parameter vector
is Gaussian in the
observables; here
µ is the vector of mean values of the observables,
C is their covariance matrix, and ,i
denotes a derivative with respect to ith model parameter
pi. The parameter vector
 includes both
cosmological and any other model parameters needed to characterize the
observations. This expression often simplifies — for example, for
N observable quantities with mean values
O
includes both
cosmological and any other model parameters needed to characterize the
observations. This expression often simplifies — for example, for
N observable quantities with mean values
O and
a covariance matrix C
that does not depend on the cosmological parameters, the Fisher matrix
becomes Fij =
and
a covariance matrix C
that does not depend on the cosmological parameters, the Fisher matrix
becomes Fij =

 ,
,  (
( O
O /
/  pi)
C
pi)
C
 -1(
-1( O
O /
/  pj).
pj).
By the Cramer-Rao inequality, a model parameter pi cannot be measured to a precision better than 1 / (Fii)1/2 when all other parameters are fixed, or a precision (Fii-1)1/2 when all other parameters are marginalized over. In practice, the Fisher matrix is a good approximation to the uncertainties as long as the likelihood can be approximated by a Gaussian, which is generally the case near the peak of the likelihood and therefore in cases when the parameters are measured with small errors. Conversely, if the errors are large, then the likelihood is typically non-Gaussian, and the constraint region is no longer elliptical but characteristically banana-shaped, as in Fig. 8. In this case, the Fisher matrix typically underestimates the true parameter errors and degeneracies, and one should employ a Monte Carlo approach to error estimation.