4. CURRENT STATUS

Since the supernova discoveries were announced in 1998, the evidence for an accelerating Universe has become substantially stronger and more broadly based. Subsequent supernova observations have reinforced the original results, and new evidence has accrued from other observational probes. In this section, we review these developments and discuss the current status of the evidence for cosmic acceleration and what we know about dark energy. In Section 7, we address the probes of cosmic acceleration in more detail, and we discuss future experiments in Section 8.

4.1. Cosmic microwave background and large-scale structure

An early and important confirmation of accelerated expansion was the independent evidence for dark energy from measurements of CMB anisotropy [Jaffe et al. 2001, Pryke et al. 2002] and of large-scale structure (LSS). The CMB constrains the amplitude of the primordial fluctuations that give rise to the observed structure as well as the distance to the last-scattering surface, r(z 1100). In order to allow sufficient growth of the primordial perturbations and not disrupt the formation of large-scale structure, dark energy must come to dominate the Universe only very recently (see Section 2.3), implying that its energy density must evolve with redshift more slowly than matter. This occurs if it has negative pressure, w < 0, cf. Eq. (5). Likewise, the presence of a component with large negative pressure that accounts for three-quarters of the critical density affects the distance to the last-scattering surface.

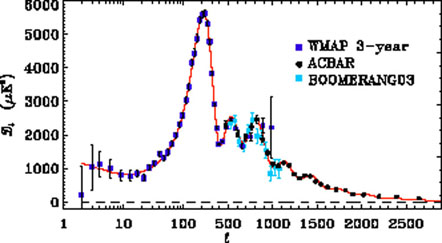
4.1.1 CMB     Anisotropies of the cosmic microwave background provide a record of the Universe at a simpler time, before structure had developed and when photons were decoupling from baryons, about 380,000 years after the Big Bang [Hu & Dodelson 2002]. The angular power spectrum of CMB temperature anisotropies, measured most recently by WMAP [Spergel et al. 2007] and by ground-based experiments that probe to smaller angular scales, is dominated by acoustic peaks that arise from gravity-driven sound waves in the photon-baryon fluid (see Fig. 5a). The positions and amplitudes of the acoustic peaks encode a wealth of cosmological information. They indicate that the Universe is nearly spatially flat to within a few percent. In combination with LSS or with independent H₀ measurement, the CMB measurements indicate that matter contributes only about a quarter of the critical density. A component of missing energy that is smoothly distributed is needed to square these observations - and is fully consistent with the dark energy needed to explain accelerated expansion.

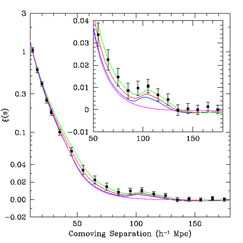Figure 5. Left panel: Angular power spectrum measurements of the CMB temperature fluctuations from WMAP, Boomerang, and ACBAR. Red curve shows the best-fit CDM model. From [Reichardt et al. 2008]. Right panel: Detection of the baryon acoustic peak in the clustering of luminous red galaxies in the SDSS [Eisenstein et al. 2005]. Shown is the two-point galaxy correlation function in redshift space; inset shows an expanded view with a linear vertical axis. Curves correspond to CDM predictions for M h2=0.12 (green), 0.13 (red), and 0.14 (blue). Magenta curve shows a CDM model without BAO.

4.1.2. Large-scale Structure     Baryon acoustic oscillations (BAO), so prominent in the CMB anisotropy, leave a subtler characteristic signature in the clustering of galaxies, a bump in the two-point correlation function at a scale ~ 100 Mpc that can be measured today and in the future can provide a powerful probe of dark energy (see Section 7.3). Measurement of the BAO signature in the correlation function of SDSS luminous red galaxies (see Fig. 5b) constrains the distance to redshift z = 0.35 to a precision of 5% [Eisenstein et al. 2005]. This measurement serves as a significant complement to other probes, as shown in Fig.8.

The presence of dark energy affects the large-angle anisotropy of the CMB (the low- multipoles) through the integrated Sachs-Wolfe (ISW) effect. The ISW arises due to the differential redshifts of photons as they pass through time-changing gravitational potential wells, and it leads to a small correlation between the low-redshift matter distribution and the CMB anisotropy. This effect has been observed in the cross-correlation of the CMB with galaxy and radio source catalogs [Boughn & Crittenden 2004, Fosalba & Gaztanaga 2004, Afshordi, Loh & Strauss 2004, Scranton et al. 2003]. This signal indicates that the Universe is not described by the Einstein-de Sitter model (_M = 1), a reassuring cross-check.

Weak gravitational lensing [Schneider 2006, Munshi et al. 2006], the small, correlated distortions of galaxy shapes due to gravitational lensing by intervening large-scale structure, is a powerful technique for mapping dark matter and its clustering. Detection of this cosmic shear signal was first announced by four groups in 2000 [Bacon, Refregier & Ellis 2000, Kaiser, Wilson & Luppino 2000, Van Waerbeke et al. 2000, Wittman et al. 2000]. Recent lensing surveys covering areas of order 100 square degrees have shed light on dark energy by pinning down the combination ₈ (_M / 0.25)^0.6 0.85 ± 0.07, where ₈ is the rms amplitude of mass fluctuations on the 8 h^-1 Mpc scale [Jarvis et al. 2006, Hoekstra et al. 2006, Massey et al. 2007]. Since other measurements peg ₈ at 0.8, this implies that _M 0.25, consistent with a flat Universe dominated by dark energy. In the future, weak lensing has the potential to be the most powerful probe of dark energy [Huterer 2002, Hu 2002], and this is discussed in Section 7 and Section 8.

4.2. Recent supernova results

A number of concerns were raised about the robustness of the first SN evidence for acceleration, e.g., it was suggested that distant SNe could appear fainter due to extinction by hypothetical grey dust rather than acceleration [Drell, Loredo & Wasserman 2000, Aguirre 1999]. Over the intervening decade, the supernova evidence for acceleration has been strengthened by results from a series of SN surveys. Observations with the Hubble Space Telescope (HST) have provided high-quality light curves [Knop et al. 2003] and have extended SN measurements to redshift z 1.8, providing evidence for the expected earlier epoch of deceleration and disfavoring dust extinction as an alternative explanation to acceleration [Riess et al. 2001, Riess et al. 2004, Riess et al. 2007]. Two large ground-based surveys, the Supernova Legacy Survey (SNLS) [Astier et al. 2006] and the ESSENCE survey [Miknaitis et al. 2007], have been using 4-meter telescopes to measure light curves for several hundred SNe Ia over the redshift range z ~ 0.3-0.9, with large programs of spectroscopic follow-up on 6- to 10-m telescopes. Fig. 6 shows a compilation of SN distance measurements from these and other surveys. The quality and quantity of the distant SN data are now vastly superior to what was available in 1998, and the evidence for acceleration is correspondingly more secure (see Fig. 8).

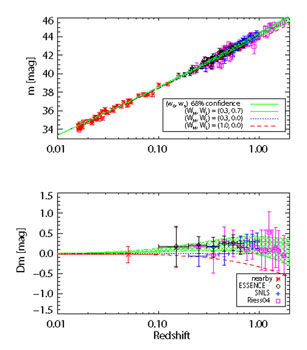Figure 6. SN Ia results: ESSENCE (diamonds), SNLS (crosses), low-redshift SNe (*), and the compilation of [Riess et al. 2004] which includes many of the other published SN distances plus those from HST (squares). Upper: distance modulus vs. redshift measurements shown with three cosmological models: M = 0.3, = 0 (dotted); M = 1, = 0 (dashed); and the 68% CL allowed region in the w0 - wa plane, assuming spatial flatness and a prior of M = 0.27 ± 0.03 (hatched). Lower: binned distance modulus residuals from the M = 0.3, = 0 model. Adapted from [Wood-Vasey et al. 2007].

4.3. X-ray clusters

Measurements of the ratio of X-ray emitting gas to total mass in galaxy clusters, f_gas, also indicate the presence of dark energy. Since galaxy clusters are the largest collapsed objects in the universe, the gas fraction in them is presumed to be constant and nearly equal to the baryon fraction in the Universe, f_{gas B} / _M (most of the baryons in clusters reside in the gas). The value of f_gas inferred from observations depends on the observed X-ray flux and temperature as well as the distance to the cluster. Only the "correct cosmology" will produce distances which make the apparent f_gas constant in redshift. Using data from the Chandra X-ray Observatory, [Allen et al. 2004, Allen et al. 2007] determined to a 68% precision of about ± 0.2, obtaining a value consistent with the SN data.

4.4. Age of the Universe

Finally, because the expansion age of the Universe depends upon the expansion history, the comparison of this age with independent age estimates can be used to probe dark energy. The ages of the oldest stars in globular clusters constrain the age of the Universe: 12 Gyr t₀ 15 Gyr [Krauss & Chaboyer 2003]. When combined with a weak constraint from structure formation or from dynamical measurements of the matter density, 0.2 < _M < 0.3, a consistent age is possible if -2 w -0.5; see Fig. 7. Age consistency is an important crosscheck and provides additional evidence for the defining feature of dark energy, large negative pressure. CMB anisotropy is very sensitive to the expansion age; in combination with large-scale structure measurements, for a flat Universe it yields the tight constraint t₀ = 13.8 ± 0.2 Gyr [Tegmark et al. 2006].

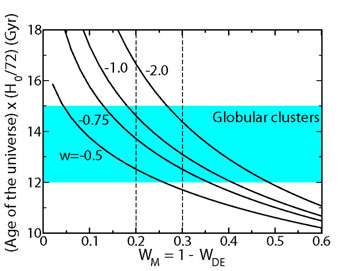Figure 7. Expansion age of a flat universe vs. M for different values of w. Shown in blue are age constraints from globular clusters [Krauss & Chaboyer 2003], and vertical dashed lines indicate the favored range for M. Age consistency obtains for -2 w -0.5.

4.5. Cosmological parameters

[Sandage 1970] once described cosmology as the quest for two numbers, H₀ and q₀, which were just beyond reach. Today's cosmological model is described by anywhere from 4 to 20 parameters, and the quantity and quality of cosmological data described above enables precise constraints to be placed upon all of them. However, the results depend on which set of parameters are chosen to describe the Universe as well as the mix of data used.

For definiteness, we refer to the "consensus cosmological model" (or CDM) as one in which k, H₀, _B, _M, , t₀, ₈, and n_S are free parameters, but dark energy is assumed to be a cosmological constant, w = -1. For this model, [Tegmark et al. 2006] combined data from SDSS and WMAP to derive the constraints shown in the second column of Table 1.

Table 1: Cosmological parameter constraints from [Tegmark et al. 2006].

Parameter	Consensus model	Fiducial model
0	1.003 ± 0.010	1 (fixed)
DE	0.757 ± 0.021	0.757 ± 0.020
M	0.246 ± 0.028	0.243 ± 0.020
B	0.042 ± 0.002	0.042 ± 0.002
8	0.747 ± 0.046	0.733 ± 0.048
nS	0.952 ± 0.017	0.950 ± 0.016
H0 (km/s/Mpc)	72 ± 5	72 ± 3
T0 (K)	2.725 ± 0.001	2.725 ± 0.001
t0 (Gyr)	13.9 ± 0.6	13.8 ± 0.2
w	-1 (fixed)	-0.94 ± 0.1
q0	-0.64 ± 0.03	-0.57 ± 0.1

To both illustrate and gauge the sensitivity of the results to the choice of cosmological parameters, we also consider a "fiducial dark energy model", in which spatial flatness (k = 0, ₀ = 1) is imposed, and w is assumed to be a constant that can differ from -1. For this case the cosmological parameter constraints are given in the third column of Table 1.

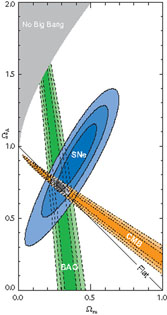
Although w is not assumed to be -1 in the fiducial model, the data prefer a value that is consistent with this, w = -0.94 ± 0.1. Likewise, the data prefer spatial flatness in the consensus model in which flatness is not imposed. For the other parameters, the differences are small. Fig. 8 shows how different data sets individually and in combination constrain parameters in these two models; although the mix of data used here differs from that in Table 1 (SNe are included in Fig. 8), the resulting constraints are consistent.

Regarding Sandage's two numbers, Table 1 reflects good agreement with but a smaller uncertainty than the direct H₀ measurement based upon the extragalactic distance scale, H₀ = 72 ± 8 km/s/Mpc [Freedman et al. 2001]. However, the parameter values in Table 1 are predicated on the correctness of the CDM paradigm for structure formation. The entries for q₀ in Table 1 are derived from the other parameters using Eq. (6). Direct determinations of q₀ require either ultra-precise distances to objects at low redshift or precise distances to objects at moderate redshift. The former is still beyond reach, while for the latter the H₀ / q₀ expansion is not valid.

Figure 8. Left panel: Constraints upon M and in the consensus model using BAO, CMB, and SNe measurements. Right panel: Constraints upon M and constant w in the fiducial dark energy model using the same data sets. From [Kowalski et al. 2008].

If we go beyond the restrictive assumptions of these two models, allowing both curvature and w to be free parameters, then the parameter values shift slightly and the errors increase, as expected. In this case, combining WMAP, SDSS, 2dFGRS, and SN Ia data, [Spergel et al. 2007] find w = -1.08 ± 0.12 and ₀ = 1.026_-0.015^+0.016, while WMAP+SDSS only bounds H₀ to the range 61-84 km/s/Mpc at 95% confidence [Tegmark et al. 2006], comparable to the accuracy of the HST Key Project measurement [Freedman et al. 2001].

Once we drop the assumption that w = -1, there are no strong theoretical reasons for restricting attention to constant w. A widely used and simple form that accommodates evolution is w = w₀ + (1 - a)w_a (see Section 6). Future surveys with greater reach than that of present experiments will aim to constrain models in which _M, _DE, w₀, and w_a are all free parameters (see Section 8). We note that the current observational constraints on such models are quite weak. Fig. 9 shows the marginalized constraints on w₀ and w_a when just three of these four parameters are allowed to vary, using data from the CMB, SNe, and BAO, corresponding to w₀ -1 ± 0.2, w_a ~ 0 ± 1 [Kowalski et al. 2008]. While the extant data are fully consistent with CDM, they do not exclude more exotic models of dark energy in which the dark energy density or its equation-of-state parameter vary with time.

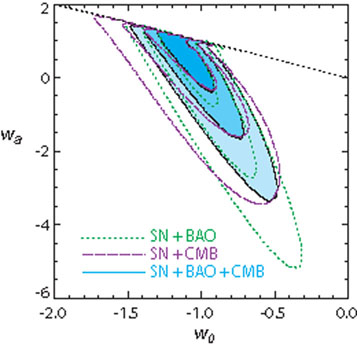Figure 9. 68.3%, 95.4%, and 99.7% C.L. marginalized constraints on w0 and wa in a flat Universe, using data from SNe, CMB, and BAO. The diagonal line indicates w0 + wa = 0. From [Kowalski et al. 2008].