Annu. Rev. Astron. Astrophys. 2004. 42: 275-316 Copyright © 2004 by Annual Reviews. All rights reserved

4. COSMIC RAY SCATTERING AND ACCELERATION IN A TURBULENT INTERSTELLAR MEDIUM

Cosmic rays scatter off magnetic waves and MHD turbulence as the particles propagate along magnetic field lines, and they generate waves and turbulence if they stream much faster than the local Alfvén speed. Observations of cosmic rays at the Earth and of radio and X-ray emissions produced by cosmic rays at their sources and throughout the Galaxy suggest the ISM is filled with irregularities on the scale of a particle gyroradius. This ranges from 1 AU to 1 pc for protons with energies between a few GeV and the knee of the cosmic ray energy distribution at 10¹⁵ eV. This section reviews the connection between cosmic rays and turbulence. It is not known if the turbulence that scatters cosmic rays has the same origin as the turbulence on larger scales, i.e., whether it is part of an energy cascade from these larger scales. It could be generated locally, for example, by the cosmic rays themselves or in other small scale instabilities (see also section 3, Interstellar Turbulence I), and it could be more similar to scintillation turbulence, which has the same small scale (Section 5) than molecular cloud turbulence, which is presumably generated on much larger scales. Other reviews of cosmic rays are in Cesarsky (1980), Berezinskii et al. (1990), Drury et al. (2001), Jokipii (2001), Ptuskin (2001), and Schlickeiser (2002).

The important point about cosmic rays from the perspective of this review is that they scatter frequently, diffusing rather than streaming through the Galaxy. Their total path length determined from the ratio of secondary to primary nuclei is equivalent to 10⁴ Galactic disk crossings at GeV energies (Engelmann et al. 1990, Higdon & Lingenfelter 2003). Their flight time determined from isotope ratios ranges from ~ 15 My for a leaky-box model with a small halo (Simpson & Garcia-Munoz 1988, Yanasak et al. 2001) to 10⁸ years for a diffusion model in a ~ 5 kpc halo (Ptuskin & Soutoul 1998). They scatter so frequently that their flux at the Earth is isotropic to within 5 × 10^-4 (Cutler & Groom 1991, Munakata et al. 1997), even though there are only a handful of nearby sources (i.e., Geminga, Vela, Lupus Loop, Loop III - see Ptuskin & Soutoul 1998, Jones et al. 2001, Taillet & Maurin 2003).

The scattering distance, , is the step size in a random walk over the Galactic thickness H (Achterberg, Blandford & Reynolds 1994). For N random isotropic scatterings, H = N^1/2 , so for total distance travelled vt = N with v ~ c particle speed, we get = H² / vt = 0.2 pc (H / kpc)² / (t / 15 My) at GeV energies. This is a very small distance on galactic scales, but still much larger than a gyroradius, R_G = _r sin mc² / (ZeB₀) for rest mass m, relativistic _r = v / c, and = (1 - _r²)^-1/2, magnetic field strength B(Gauss) and charge Ze with e = 4.803 × 10^-10 esu. In the expression for R_G, the angle of particle motion with respect to the field line is . Taking _r ~ 1 and sin ~ 1, we get R_G ~ 3.3 × 10¹² E_GeV/ (ZB _{µ G}) cm for hadron particle energy E_GeV in GeV and field strength B _{µ G} in microGauss. Thus, the mean scattering distance for GeV energies is ~ 10⁵ gyroradii and the gyroradius has the same scale as the Solar system.

The relative amplitude of the magnetic irregularities B / B₀ that have the size R_G may be determined from the random walk of angular deflections, , which build up in proportion to the square root of the number N_G of gyrations as ~ N_G^1/2 B / B for small B / B. The scattering frequency is v / = ² / t, and the number of gyrations is N_G = t for gyrofrequency = v / R_G. Thus, = (B / B)² and B / B₀ = (R_G / )^1/2 ~ 2 × 10^-3 when ~ 0.2 pc. Evidently, magnetic fluctuations of less than one percent on 0.1 AU scales can isotropize cosmic rays with GeV energies; in general, a wide spectrum of fluctuations is needed to scatter the full energy range. This level of irregularity is much smaller than observed on > 10 pc scales from pulsar dispersion measures, which suggest B ~ 5 µG and <B> ~ 1.5 µG (Rand & Kulkarni 1989). It is also smaller than the integrated fluctuations found by scintillation on scales less than 3.5 pc, which give B ~ 0.9 µG and <B> ~ 3 µG (Minter & Spangler 1997), and smaller than B / B ~ 1 from optical polarization (Heiles 1996, Fosalba et al. 2002). A spectrum of magnetic energy fluctuations like the Kolmogorov or Kraichnan spectra will make B / B much smaller on the scale of the gyroradius than these observed field irregularities. Such a spectrum will also give the required rigidity dependence for the diffusion coefficient (Strong & Moskalenko 1998). The rigidity of a cosmic ray is _r mc² / Ze.

Cosmic rays can also scatter off strong magnetic irregularities having a scale comparable to or larger than R_G (Jokipii 1987). Inverting the above expression and integrating over a spectrum of waves (k / k_min)^-q, the mean free path is ~ (B / B)² R_G(k_min R_G)^1-q (Schlickeiser 1989). For B / B ~ 1 and a particle gyroradius that fits inside the compressed region, R_G k_min^-1, this gives ~ R_G. If the scattering arises in a network of strong shocks in a supersonically turbulent medium, then the mean free path for diffusion will be about the shock separation. Because the gyroradius of GeV protons is less than the collision mean free path for atoms and ions, collisional MHD models of compressible turbulence do not apply to these small scales (see Interstellar Turbulence I and Section 4.2 below).

4.1. Cosmic Ray Scattering in Magnetic Waves

The field line fluctuations that scatter cosmic rays could be coherent waves, stochastic turbulence, or shock fronts. One common view of waves is that they are weak fluctuations compared with the mean field, with wave travel times much longer than an oscillation period and a well-defined dispersion relation between frequency and wavenumber. Particles in such a wave field interact successively with many crests, travelling rapidly along the field until their cumulative pitch angle deviation becomes large and they begin to interact with a different wave train. A turbulent medium is not so regular but particle interactions with a broad wave spectrum can be similar as long as the particle sees a magnetic perturbation with the right wavelength after each gyration. In both cases the field can be treated as static for the fast-moving particles.

Much of the history of cosmic ray theory is based on observations of the solar wind, which contains a mixture of weak and strong fluctuations, depending on frequency (Dröge 1994; Goldstein, Roberts & Matthaeus 1995). Perhaps ~ 15% of it is in the form of slab-like Alfvén waves (k ~ 0) and ~ 85% is two-dimensional (2D) magnetic turbulence (k_|| ~ 0, Bieber, Wanner & Matthaeus 1996). Here, k and k_|| are wavenumbers perpendicular and parallel to the mean field. The solar wind observations led to the quasilinear theory of cosmic ray propagation (Jokipii 1966), which assumes the field is uniform in space and unchanging in time over a particle gyration. Interstellar applications of this theory may be appropriate at high spatial frequencies where weak electron perturbations scatter radio waves (Section 5), or near shock fronts where weak waves on either side scatter relativistic particles back and forth (Section 4.3), or for waves that are excited by the cosmic rays themselves (Chandran 2000a). The waves cause cosmic rays to diffuse in both momentum and space (e.g., Schlickeiser 1994). Momentum diffusion means that velocities change and isotropize; space diffusion means that cosmic rays spread out slowly to more uniform densities. The two diffusion coefficients are inversely related: Higher momentum diffusion means lower spatial diffusion as the particles isotropize their velocities more easily.

There are two types of waves that could be important for cosmic ray scattering. Alfvén waves are transverse oscillations with a restoring force from field line tension and a frequency less than the ion gyro frequency. Their dispersion relation between frequency and wavenumber k is ² = v_A² k² cos² for angle between the wave propagation vector and the average field. Their group and phase velocity parallel to the mean field is the Alfvén speed v_A = B / (4 _i)^1/2 for ion density _i. When thermal pressure with sound speed a contributes to the restoring force there are also magnetosonic waves with the dispersion relation

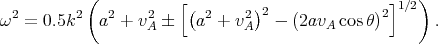(6)

The positive and negative signs are for fast and slow waves. For oblique propagation of magnetosonic waves, when cos ~ 0, the phase speed of the fast mode can be large along the field lines: v_A / cos in the low limit ( is the ratio of thermal to magnetic pressures, = 2(a / v_A)²) and a / cos in the high limit. This speed is important for cosmic rays because they also move quickly along the field lines and will resonate with the magnetic fluctuations in these waves. Oblique magnetosonic waves also have a magnetic pressure that varies slightly along the field as a result of the successive convergences and divergences of the velocity and field, which are in phase for fast waves and out of phase for slow waves. These field line changes create magnetic mirrors that enhance the scattering (Schlickeiser & Miller 1998, Ragot 2000).

The condition for resonance between a cosmic ray and a wave is (Jokipii 1966, Hall & Sturrock 1967, Hasselmann & Wibberenz 1968)

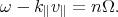(7)

This expression says that the Doppler shifted frequency of the magnetic wave, as viewed by the particle moving parallel to the field at speed v_|| = v µ vcos for pitch angle , equals an integer number, n, of the gyration frequency. For an Alfvén wave, = k_|| v_A, and for a fast mode at low , = k v_A. The case |n| 1 is gyroresonance. For wave spectra that decrease with k as a power law, only the lowest-order resonances (n = ± 1) are important (Cesarsky & Kulsrud 1973).

Magnetosonic waves have an additional resonance for n = 0 (Lee & Völk 1975, Fisk 1976, Achterberg 1981), when particles stay between two crests by moving along the field at the parallel wave speed. Such a particle slows down when it hits the compressive part of the wave ahead of it (by the mirror effect), and it speeds up if the compressive part hits the particle from behind. As a particle oscillates between crests, it can have a parallel velocity that resonates with another wave moving faster along the field, and then jump over to become trapped between two new crests. For a broad wave spectrum, the particle jumps from one wave to the next, gaining energy on average. This process is called transit time acceleration of particles or transit time damping (TTD) of waves (Miller 1997, Schlickeiser & Miller 1998). TTD increases the parallel component of cosmic ray momentum by mirror scattering in the wave frame. The mirror force depends on the square of the perpendicular component of the velocity (Section 4.2), so TTD must operate with the pitch-angle scattering of gyroresonance to maintain momentum isotropy (Miller 1997).

A particle that interacts with an Alfvén wave can resonate only with the wavelength that is equal to the parallel gyrolength in the Doppler shifted frame, (v_A - v_||)2 / . A particle that interacts with magnetosonic waves can respond to the whole wave spectrum because it can choose the wave direction where the parallel wave speed equals its own (Schlickeiser & Miller 1998, Schlickeiser & Vainio 1999). In practice, such a wave field may not have the appropriate because wave damping is larger at higher .

TTD was originally thought to be such an important energy loss for the waves that the fast mode would not be important for cosmic rays (Schlickeiser 1994, Minter & Spangler 1997, Tsap 2000). Damping is large for high because the thermal particles resonate with the waves and only highly parallel modes exist (Holman et al. 1979, Foote & Kulsrud 1979). However, << 1 in the solar wind and in much of the cool dense phase of the ISM, and observations of the solar wind show that oblique and fast modes dominate over plane-parallel Alfvén waves (Tu, Marsch & Thieme 1989; Bieber, Wanner & Matthaeus 1996; Matthaeus, Goldstein & Roberts 1990). Thus, TTD particle acceleration could be important in parts of the ISM where is small. The waves still have to be nearly isotropic to get effective scattering, though, and they should not be damped by other processes, such as ion-neutral or viscous friction. Such damping is important in most of the neutral medium where < 1 is otherwise favorable for TTD (Kulsrud & Pearce 1969, Felice & Kulsrud 2001). This leaves few places where wave damping is low enough that TTD might be important.

Alfvén wave scattering is questionable too because of the extreme anisotropy of the fluctuations that may cascade down from pc scales to the gyroradius. Anisotropic turbulence produces tiny perpendicular irregularities that average out over a particle gyration (Chandran 2000a, 2001; Lerche & Schlickeiser 2001; Yan & Lazarian 2002; Teufel, Lerche & Schlickeiser 2003). The result is a scattering coefficient that is many orders of magnitude less than in the isotropic case. For this reason, Yan & Lazarian (2003a) reconsidered TTD scattering by fast modes at moderate , emphasizing the isotropy of the fast waves and considering ISM regions where wave damping at particular cosmic ray energies is relatively small. The resolution of this damping problem for wave scattering is far from clear.

4.2. Other Scattering Mechanisms

The energy of fast cosmic ray gyrations is adiabatically invariant during slow changes in the magnetic field amplitude, so an increasing field puts more energy into the gyromotion while removing it from the parallel motion. This change, combined with momentum conservation, causes fast particles with high pitch angles to bounce off converging field lines. The mirror force is -M_|| B for magnetic moment M = mv² / 2B with particle mass m. This type of scattering involves very long wavelengths parallel to the field (Ragot 1999, 2000; Felice & Kulsrud 2001; Lu et al. 2002). The mirror sources could also be molecular clouds and clumps (Chandran 2000b).

Electric fields can also scatter cosmic rays. The flow of plasma at speed U transverse to a magnetic field generates an electric field, E = -u × B, that can be important in the parallel direction when the magnetic field has at least 2D structure, and it is convected around by turbulent motions (Fedorov et al. 1992, le Roux et al. 2002).

Transport transverse to the mean field occurs as individual field lines wander (Jokipii & Parker 1969, Bieber & Matthaeus 1997, Michalek & Ostrowski 1998, Giacalone & Jokipii 1999, Kóta & Jokipii 2000). This is important for radial diffusion in the solar wind, which has a spiral field (Chen & Bieber 1993), for diffusion in oblique shock fronts (Duffy et al. 1995), and for diffusion in the vertical direction out of the Galaxy. Magnetic fields with irregularities smaller than the gyroradius cause particles to skip over field lines, giving anomalous diffusion (Parker 1964; Chuvilgin & Ptuskin 1993; Casse, Lemoine & Pelletier 2002; Otsuka & Hada 2003; Erlykin et al. 2003). Braided field lines can lead to sub-diffusion (Getmantsev 1963), when the mean squared particle position in the cross field direction increases as the square root of time, instead of directly with time as in normal diffusion. Compound diffusion has both cross-field diffusion and diffusion along the field lines (Kirk et al. 1996). Cross diffusion requires a lot of perpendicular structure to the field lines over a diffusion length for the particle motion parallel to the field (Qin, Matthaeus & Bieber 2002). For ISM turbulence, the cross-field diffusion coefficient is 0.1-0.2 of the parallel coefficient (Chandran & Maron 2004a).

Shocks provide another site for cosmic ray scattering. Blandford & Ostriker (1980) considered an ISM made of cleared hot cavities from supernovae and showed how the resulting shocks could scatter and accelerate cosmic rays. Bykov & Toptygin (1985) extended this model to include secondary shocks that arise in the turbulence caused by the supernovae. Klepach, Ptuskin & Zirakashvili (2000) included stellar wind shocks. The composite spectrum of cosmic rays from an ensemble of shocks in a supersonically turbulent medium was determined by Schneider (1993). In such a medium, the summed energy distribution for cosmic rays from all of the shocks is close to a power law, but there can be flat parts or bumps, unlike the energy distribution from a single shock (see also Achterberg 1990, Bykov & Toptygin 1993).

4.3. Cosmic Ray Acceleration

Cosmic rays gain energy as they scatter off randomly moving parts of the ISM (Fermi 1949). This is momentum diffusion and called the second-order Fermi mechanism because the energy gained per collision depends on the second power of the rms turbulent speed. It is reminiscent of the thermalization of a star cluster with the light particles gaining speed as they approach equilibrium with the heavy particles. Scott & Chevalier (1975) first applied this mechanism to supernova remnants, using random motions inside the remnant for scattering sites. Supernovae are a likely source for cosmic rays because the cosmic ray energy density, ~ 1 eV cm^-3, divided by a ~ 15 My lifetime in the Galaxy, is about 5% of the total supernova power (Baade & Zwicky 1934, Ginzburg & Syrovatskii 1964).

Cosmic ray acceleration by momentum diffusion occurs throughout a compressibly turbulent ISM, not just in supernova remnants (Kulsrud & Ferrari 1978, Ptuskin 1988, Dolginov & Silant'ev 1990, Bykov & Toptygin 1993, Webb et al. 2003, Chandran & Maron 2004b). In a system of many shocks, particles that are trapped in the weak magnetic turbulence of the ambient medium also get accelerated every time these regions are compressed (Jokipii 1987).

Multiple shock crossings at the edge of a supernova remnant also accelerate cosmic rays (see review in Blandford & Eichler 1987). If the field is parallel to the shock direction, then magnetic turbulence created ahead of the shock by the outward streaming particles (Wentzel 1974, Skilling 1975) scatters these particles back into the shock where they encounter more turbulence. The post-shock turbulence was formerly pre-shock turbulence that got compressed and amplified (Schlickeiser, Campeanu & Lerche 1993; Vainio & Schlickeiser 1998). If the field is oblique to the shock direction, then gyromotions (Jokipii 1987) and field line wandering cycle particles through the front (Ragot 2001). Each time a particle cycles through the front it gains energy from the converging flow. This is called the first-order Fermi mechanism (Fermi 1954) because the energy gained per crossing depends on the first power of the shock velocity. About 10^-3 of the incoming thermal particles are injected into cosmic rays (Pryadko & Petrosian 1997; Kang, Jones & Gieseler 2002; Bamba et al. 2003), with an efficiency depending on obliqueness (Ellison, Baring & Jones 1995; Kobayakawa, Honda, Samura 2002). Generally, the first-order mechanism dominates in strong shocks (Axford et al. 1977, Krymsky 1977, Bell 1978, Ostrowski 1994), although the second mechanism is more important downstream than upstream (Vainio & Schlickeiser 1998).

Shock acceleration explains the cosmic ray energy spectrum up to the "knee" at ~ 10¹⁵ eV. The particles that stay in the shock longest end up with the most energy. The spectrum is a distribution function in the number of shock crossings, considering the continuous loss of particles that are trapped in the downstream flow (e.g., Kato & Takahara 2003).

Observations of the edge sharpness of supernova remnants suggest the amplitude of MHD waves near the shock is ~ 60 times the average ISM value (Achterberg, Blandford & Reynolds 1994). Simonetti (1992) observed a factor of at least 10 in the magnetic wave amplitude from Faraday rotation irregularities in a supernova remnant compared with the adjacent line of sight. The X-ray synchrotron emission from supernova remnants is direct evidence for acceleration of relativistic electrons (Koyama et al. 1995, Aschenbach & Leahy 1999).

4.4. Generation of Turbulence by Cosmic Rays

A collection of particles with a high enough density cannot stream along a magnetic field much faster than the Alfvén speed because they generate magnetic irregularities that scatter them (Lerche 1967; Wentzel 1968a, 1969; Kulsrud & Pearce 1969; Tademaru 1969). The growth rate of the instability at wavenumber k for isotropic wave generation is (Cesarsky 1980)

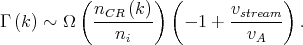(8)

The first term in the parenthesis represents the stabilizing effect of wave damping from ion gyromotions. The second term drives the instability with a rate proportional to the ratio of the streaming speed to the Alfvén speed. The influence of collective effects is in the ratio of the density of those cosmic rays that resonate with wavenumber k to the background density of thermal ions. The size of the magnetic irregularity produced is about 2 times the particle gyroradius (~ 10¹³ cm for GeV energy and µGauss field), so more energetic particles make larger-scale field distortions. These distortions are not at the bottom of a turbulent cascade, so they should not be anisotropic (Chandran 2000a). They could cascade to give the ISM scintillation. The upper limit to the cosmic ray energy that can generate waves sufficient for their own scattering is around 100 to 1000 Gev (Cesarsky 1980, Yan & Lazarian 2003a). Much higher energies are possible in a Galactic wind model where the boundary between diffusion and advection depends on energy and the streaming instability Landau damps in a highly ionized Galactic halo (Ptuskin et al. 1997).

Hall (1980) suggested that waves generated by cosmic rays would damp quickly and proposed instead that scintillation-scale structures result from mirror and firehose instabilities in the hot ISM phase. Both require pressure anisotropies, which Hall notes should arise at the level of 0.01-0.1 if the hot medium is turbulent. The firehose instability requires P_|| - P >B² / 4 for parallel and perpendicular pressures P_|| and P (Lerche 1966, Wentzel 1968b), and the mirror instability requires P - P_| > (B² / 4)(P_|| / B). These conditions are satisfied for anisotropy |P_||-P| / 2P_|| ~ 0.01-0.1 if the plasma = P / P_mag is very large, as might be the case in the hot intercloud medium if supernovae continuously sweep it free of gas and field.