Annu. Rev. Astron. Astrophys. 2004. 42: 275-316 Copyright © 2004 by Annual Reviews. All rights reserved

5. RADIO WAVE SCINTILLATION AS A DIAGNOSTIC FOR ISM TURBULENCE

One of the earliest indications that the ISM is turbulent came from scintillation observations of electron density fluctuations on very small scales. These fluctuations cause diffraction and refraction of radio signals from pulsars and a few extragalactic sources. Diffraction broadens pulsar images, spreads out the pulse arrival times, and narrows the frequency interval over which the pulses have a coherent behavior. The relative motion of the diffracting medium also modulates the pulsar intensity on a timescale of minutes. Refraction from larger structures causes the images to split or wander in position and to vary in intensity on timescales of days to months. Scintillation effects like these offer many diagnostics for electron density structures in the ionized interstellar medium, including H II regions, hot bubble edges and the ionized and hot intercloud media. Still, the origin of this turbulence is not clear. Because the scales are very small, typically 10¹⁵ cm or below, it could be part of a cascade from larger structures past the viscous length and down into the collisionless regime of MHD turbulence (section 4.11 in Interstellar Turbulence I), or it could be generated locally by cosmic ray streaming or other small-scale instabilities or by low-mass stellar winds and wakes (sections 3 and 4 in Interstellar Turbulence I). Here we review ISM scintillations. More extensive reviews may be found in Rickett (1977, 1990), Hewish (1992), and Cordes, Rickett & Backer (1988).

5.1. Theory of Diffraction and Refraction in the ISM

The index of refraction for radio waves is (Nicholson 1983)

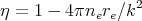(9)

with electron density n_e, classical electron radius r_e = e² / (m_e c²) = 2.8 × 10^-13 cm, and wavenumber of the radio signal k = 2 / for wavelength . The phase change of a signal that passes through a clump of size x with an excess index of refraction compared with a neighboring average region is kx . The transmitted signal adds constructively to the neighboring signal at a relative propagation angle if the difference in their path lengths, x sin, multiplied by k, equals the phase change. This gives ~ = 4 n_e r_e / k² for small . This phase change is random for each clump the signal meets, so after N = D / x such clumps on a path length D, the root mean square angular change of the signal from diffraction is _d = N^1/2.

The most important clump size has a cumulative scattering angle (D / x)^1/2 equal to the clump diffraction angle, _d = (kx)^-1. Evaluation of requires some knowledge of how n_e depends on x. For a turbulent medium, this relation comes from the power spectrum of electron density fluctuations,

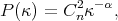(10)

where = 1 / x and = 11/3 for 3D turbulence with a Kolmogorov spectrum (we use here for the wavenumber of electron density fluctuations to distinguish it from the wavenumber k of the radio radiation used for the observation). The mean squared electron density fluctuation is obtained from the integral over phase space volume, P() 4 ² d. For logarithmic intervals, this is approximately n_e² = P() 4 ³ ~ 4 C_n² x^-3. Thus, we have x ~ (16 ² r_e² DC_n²)^{-1 / (-2)}. Using the wave equation, Cordes, Pidwerbetsky & Lovelace (1986) got essentially the same result with 4² replacing 16. The full theory more properly accounts for differences in the cumulative effects of the line-of-sight and transverse density variations. A recent modification considers power-law rather than Gaussian statistics for the clump size distribution (Boldyrev & Gwinn 2003).

For a reference set of parameters, e.g., GHz frequencies, kpc distances, and typical C_n² ~ 10^-4 meters^-20/3, the characteristic scale is x ~ 10¹⁰ cm. This small size implies that only pulsars and a few extragalactic radio sources can produce detectible diffraction effects at radio frequencies. The smallness compared with the collisional mean free path of electrons also implies that the fluctuations have to be collisionless (see Interstellar Turbulence I).

Many observable properties of small radio sources give information, either directly or indirectly, about x, which can be used to infer the strength and power index of the electron density fluctuation spectrum and its distribution on the line of sight. For example, the logarithm of the visibility of an interferometer is -4^{2 2} r_e² s^-2 SM where s is the baseline length and SM = ₀^D C_n² dz is the scattering measure. Spangler & Cordes (1998) found ~ 3.65 ± 0.08 using this baseline dependence for 4 pulsars. Very long baseline interferometry (VLBI) observations of pulsar image sizes measure angular broadening as a function of frequency (Lee & Jokipii 1975a; Cordes, Pidwerbetsky & Lovelace 1986) and determine SM (Spangler et al. 1986). For the reference parameters, _d ~ 0.15 mas.

Angular broadening gives a spread in path lengths for the radio waves, and this corresponds to a spread in arrival times of pulses, = D_d² / (2c) (Lee & Jokipii 1975b). Such pulse broadening scales as ^{2 / (-2)} SM^{2 / (-2)} D, so the frequency dependence gives and the absolute value gives SM for an assumed screen depth D. The flux density is correlated only over a small range of frequencies, _d ~ (2 )^-1 (Salpeter 1969, Lee & Jokipii 1975b).

Pulsar amplitudes vary on a timescale t_d = x / v ~ several minutes as a result of pulsar transverse motions v ~ 100 km s^-1 (Cordes 1986). Using the relations above, this can be rewritten t_d ~ (cD _d )^1/2 / (2^1/2 v). If pulsar distances and proper motions are also known, along with the dispersion measure, then the distribution of scattering material on the line of sight can be modeled (Harrison & Lyne 1993, Cordes & Rickett 1998).

Longer time variations (Sieber 1982) result from the changing refraction of radio signals in moving structures that have the diffraction angular size _d or larger (Rickett, Coles & Bourgois 1984; Blandford & Narayan 1985). This angular size corresponds to a physical size for the refracting elements x_r = D _d. For typical _d ~ 0.1 mas, x_r ~ 1.5 × 10¹² cm at D = 1 kpc. The corresponding refraction scintillation time is t_r = x_r / v ~ days. Time variations over months are also observed from larger interstellar structures.

The relative rms amplitude of the source is the modulation index, m = <(I - <I>)²>^1/2 / <I>. For diffraction this can be 100%, but for refraction it is typically less than ~ 30% (Stinebring & Condon 1990, LaBrecque et al. 1994, Stinebring et al. 2000). The modulation index depends on the strength of scattering, which involves a length scale equal to the geometric mean of the scale for angular broadening and the dominant scale for electron density fluctuations, (D _d x)^1/2. This is the Fresnel length, r_F = (D / k)^1/2, which is the transverse size of some object at distance D that is just small enough to show diffraction effects. When r_F / x_d is high, there are many diffracting elements of size x_d inside each refracting element of size D _d, so diffraction is strong. For weak diffraction, the total phase change on the line of sight is small and the dominant clump size is the Fresnel length itself (Lovelace et al. 1970, Lee & Jokipii 1975c, Rickett 1990). In this case, the modulation index scales approximately with (r_F / x_d)^-2 < 1 (Lovelace et al. 1970). The modulation index measures interstellar properties in this weak limit because then m^{2 ( + 2) / 2} D ^{/ 2}C_n², giving a diagnostic for C_n² and (Rickett 1977). Small m usually corresponds to high frequencies, where diffraction is relatively unimportant.

Time variations can be visualized with a dynamic spectrum, which is a gray scale plot of intensity on a coordinate system of time versus frequency (Figure 2). Diffraction alone gives a random dynamic spectrum from the motion of unresolved objects of size x, but larger refractive structures, which disperse their radio frequencies over larger angles, ~ -2 / (from the above expression ~ 4 n_e r_e / k²), sweep a spectrum of frequencies past the observer (Hewish 1980). The intensity peaks on a dynamic spectrum (averaged over many pulses) then appear as streaks with slope dt / d = -2D _d / ( v) (Cordes, Pidwerbetsky & Lovelace 1986); this can be used as a diagnostic for v. The right-hand part of Figure 2 is the 2D power spectrum of the dynamic spectrum. Stinebring et al. (2001) and Hill et al. (2003) suggest that the arcs arise from interference between a central image and a faint scattering halo 20-30 times larger.

Figure 2. Dynamic spectrum of pulsar PSR B1929+10 (left) plotting flux density linearly with grayscale. The vertical columns are spectra, and many spectra are aligned horizontally in time. Intervening fluctuations in the electron density cause the signal to drift in both frequency and arrival time. A 2D Fourier transform of the dynamic spectrum is shown on the right. The crisscross pattern in the dynamic spectrum causes the parabolic boundary in the Fourier transform distribution. The grayscale for the secondary spectrum is logarithmic from 3 dB above the noise to 5 dB below the maximum (from Hill et al. 2003).

Strong refraction can result in multiple images that produce interference fringes on a dynamic spectrum (Cordes & Wolszczan 1986; Rickett, Lyne & Gupta 1997). Multiple images imply that refraction, which determines the image separation, bends light more than diffraction, which determines the size. Because large-scale fluctuations dominate refraction, this observation implies either > 4, so that small wavenumbers dominate (Cordes, Pidwerbetsky & Lovelace 1986; Romani, Narayan & Blandford 1986), or there is additional structure on 10¹² cm scales that is not part of a power law power spectrum (Rickett, Lyne & Gupta 1997).

5.2. Observations

Radio scintillation has been used to determine many properties of electron density fluctuations in the ISM. Diffraction and refraction come from the same electrons, so the ratio of their strengths is proportional to the ratio of the amplitudes of the electron density fluctuations on two different scales. From this ratio Armstrong, Rickett & Spangler (1995) derived the power spectrum of the fluctuations spanning > 6 orders of magnitude in scale. They determined C_n² = 10^-3 m^-20/3 and = 11/3 between 10⁶ cm and 10¹³ cm. They also suggested from rotation measures (RM = ₀^D n_e B_|| dz) that the same power law extends up to 10¹⁷ or 10¹⁸ cm.

Cordes, Weisberg & Boriakoff (1985) found = 3.63 ± 0.2 using the relation between _d and . They mapped the spatial distribution of C_n² from _d observations of 31 pulsars, suggesting the Galaxy contains both thin and thick disk components. For the thin component, C_n² ~ 10^-3-1 m^-20/3 assuming = 11/3 and for the thick component, with H > 0.5 kpc, C_n² ~ 10^-3.5 m^-20/3. The rms level of electron density fluctuations at the dominant scale x ~ 10¹⁰ cm, which comes from the integral over the power spectrum (see above), was found to be <n_e²>^1/2 ~ 5 × 10^-6 cm^-3 for the high latitude medium, for which <n_e> ~ 0.03 cm^-3 from dispersion measures, and <n_e²>^1/2 ~ 10^-4.2-10^-3.3 cm^-3 for the low latitudes.

Bhat, Gupta & Rao (1998) observed 20 pulsars for three years to average over refraction variations and determined C_n² in the local ISM from _d. They observed an excess of scattering material at the edge of the local bubble, which also produced multiple images of one of these pulsars (Gupta, Bhat & Rao 1999). The edge of the local bubble may also have been seen by Rickett, Kedziora-Chudczer & Jauncey (2002) as a source of scattering in a quasar. Bhat & Gupta (2002) found a similar enhancement at the edge of Loop I, where SM ~ 0.3 pc m^-20/3 and the density enhancement is a factor of ~ 100 over the surrounding gas. They also found excess scattering for more distant pulsars from the Sagittarius spiral arm.

Lazio & Cordes (1998a, b) used the angular sizes of radio sources and other information on lines of sight to the Galactic center and outer Galaxy to suggest that the scattering material is associated with the surfaces of molecular clouds. Ionized cloud edges were also suggested by Rickett, Lyne & Gupta (1997) to explain multiple images. Spangler & Cordes (1998) observed _d from small sources behind six regions in the Cygnus OB1 association and found an excess in SM that was correlated with the emission measure, indicating again that scattering is associated with H II regions. This result is consistent with the high cooling rate required by the dissipation of this turbulence, which implies high temperatures (Zweibel, Ferriere & Shull 1988; Spangler 1991; Minter & Spangler 1997).

The relation v ~ (cD _d )^1/2 / (2^1/2 t_d) combined with pulsar distances and proper motions led Gupta (1995) to determine a 1 kpc scale height for the scattering layer from long-term observations of 59 pulsars. Cordes & Rickett (1998) also used this method to find that scattering is rather uniformly distributed toward two pulsars, but for three lines of sight it was concentrated toward the pulsar, including Vela where the supernova remnant is known to contribute to the scattering (Desai et al. 1992); six other pulsars in that study had significant scattering from either a foreground spiral arm or H II regions.

Bhat, Gupta & Rao (1999) compared _d obtained from _d with the angular size of the refraction pattern, _r ~ (v / D)(dt / d) from dynamic spectra. They showed that _r / _d < 1 for all 25 pulsars that had this data, implying that diffraction dominates refraction and therefore < 4. They also compared C_n² from _r on the refractive scale with C_n² from _d on the diffractive scale to determine the slope of the power spectrum directly (as did Armstrong et al. 1995). They found the Kolmogorov value = 11/3 to within the accuracy in most cases, but six pulsars, mostly nearby, gave slightly higher ~ 3.8. The longest-term variations had significantly more power than an extrapolation of the Kolmogorov spectrum, however, and the modulation indices were large, leading them to suggest an additional component of scattering electrons at scales of 10¹⁴ to 10¹⁵ cm. The same data led Bhat, Rao & Gupta (1999) to derive <C_n²> ~ 10^-3.8 m^-20/3 and <r_F / x_d> ~ 45, indicating strong scattering.

Lambert & Rickett (2000) looked at the correlation between the modulation index for long-term variations from refraction and the relative decorrelation bandwidth, _d / , which comes from diffraction. The correlation at 610 MHz for 28 sources fit Kolmogorov scaling ( = 11/3) better than a shock-dominated model ( = 4) model but at 100 MHz the Kolmogorov fit was not as good. They suggested that the minimum turbulent length was large, 10¹⁰ to 10¹² cm instead of < 10⁹ cm (Armstrong, Rickett & Spangler 1995). An excess of electron density structure at large scales could also explain the discrepancy.

Stinebring et al. (2000) monitored the modulation index of 21 pulsars for five years and found low values (< 50%) that bracket 3.5 < < 3.7 with no perceptible inner (smallest) scale for most of the pulsars. For the Crab, Vela, and four others, enhanced modulation indices were consistent with an inner scale of 10¹⁰ cm. Rickett, Lyne & Gupta (1997) suggested this excess scattering could be from AU-sized ionized clumps at cloud edges.

An inner scale of 5 × 10⁶ - 2 × 10⁷ cm was found by Spangler & Gwinn (1990) after noting that interferometer baselines shorter than this had scintillation with ~ 4 whereas longer baselines had near the Kolmogorov value, -11/3. They suggested the inner scale is caused by a lack of turbulence smaller than the ion gyroradius, v_th / for thermal speed v_th, or by the ion inertial length, v_A / , whichever is larger. This value of the inner scale is consistent with an origin of the scattering in the warm ionized medium or in H II regions, but not in the hot coronal medium, which has much larger minimum lengths.

Shishov et al. (2003) studied pulsar PSR B0329+54 over a wide range of frequencies and found a power spectrum for electron density fluctuations with a slope of -3.5 ± 0.05 for lengths between 10⁸ cm and 10¹¹ cm. This spectrum is expected for turbulence in the Iroshnikov-Kraichnan model (see Interstellar Turbulence I). Shishov et al. noted how other lines of sight though the galaxy gave different spectra and suggested that the nature of the turbulence varies from place to place. They also found refraction effects on a scale of 3 × 10¹⁵ cm corresponding to electron density fluctuations of strength n_e ~ 10^-2 cm^-3 and suggested these were neutral clouds with an overall filling factor of ~ 0.1.

Scattering image anisotropy suggests anisotropic turbulence (see Interstellar Turbulence I). Lo et al. (1993) observed 2:1 anisotropy in images of Sgr A^*, Wilkinson, Narayan & Spencer (1994) found scale-dependent anisotropic images of Cygnus X-3, Frail et al. (1994) observed 3:1 anisotropy in scattering of light from Galactic center OH/IR stars, whereas Trotter, Moran & Rodriguez (1998) observed axial ratios of 1.2-1.5 for quasar light that scatters through a local H II region. A ratio of 4:1 was found for another quasar by Rickett, Kedziora-Chudczer & Jauncey (2002). Spangler & Cordes (1998) observed anisotropic scattering with axial ratio of 1.8 surrounding the Cygnus OB association and Desai & Fey (2001) observed axial ratios of ~ 1.3 toward the same region. The actual anisotropy of local fluctuations cannot be determined from these observations because many different orientations blend on the line of sight (Chandran & Backer 2002)

Extreme scattering events are observed in some extragalactic radio sources and a few pulsars. Their modulation is strong, 50%, they can last for several months, and they have light profiles that are flat-bottom with spikes at the end, or smooth bottom with no spikes (Fiedler et al. 1994). They may result from supernova shocks viewed edge-on (Romani, Blandford & Cordes 1987) or ionized cloud edges in the Galaxy halo (Walker & Wardle 1998). Some appear correlated with the edges of local radio loops (Fiedler et al. 1994, Lazio et al. 2000), in support of the shock model. The actual scattering process could be a combination of refractive defocusing, during which an intervening electron cloud produces a lens that diverges the light and makes the source dimmer (Romani et al. 1987, Clegg et al. 1998), or stochastic broadening by an excess of turbulence in a small cloud (Fiedler et al. 1987). Lazio et al. (2000) found an excess SM = 10^-2.5 kpc m^-20/3 associated with an event, corresponding to C_n² ~ 10^{7 -1}(D / 100 pc)^-1 m^-20/3 for ratio of the line-of-sight extent (D) to the transverse extent. Fiedler et al. (1994) suggested <n_e²>^1/2 ~ 10² / cm^-3. This high level of scattering along with an observed increase in angular size during the brightness minimum (Lazio et al. 2000) suggests the scattering cloud is not part of a power spectrum of turbulence but is an additional AU-size feature (Lazio et al. 2000).

5.3. Summary of Scintillation

The amplitude, slope, and anisotropy of the power spectrum of interstellar electron density fluctuations have been observed by scintillation experiments. Estimates for the inner scale of these fluctuations range from 10⁷ cm to 10¹⁰ cm or more. The shorter of these lengths is about the ion gyroradius in the warm ionized medium (Spangler & Gwinn 1990). This is much smaller than the mean free path for electron collisions so the fluctuations are collisionless (see Interstellar Turbulence I). A lower limit to the largest scale of ~ 10¹⁸ cm was inferred from rotation measures assuming a continuous power law for fluctuations, but this assumption is uncertain. The slope of the power spectrum is usually close to the Kolmogorov value, -11/3, and distinct from the slope for a field of discontinuities, which is -4. Deviations from the Kolmogorov slope appear in some studies, and may be from a large inner scale, >> 10⁹ cm, an excess of scattering sites having size ~ 1-10 AU, or a transition in the scaling properties of the turbulence.

Scintillation arises from both the low-density, diffuse, ionized ISM and the higher-density H II regions, ionized cloud edges, and hot shells, where the amplitude of the power spectrum increases. On average, the relative fluctuations are extremely small, <n_e²>^1/2 / <n_e> ~ 10^-2 on scales that dominate the diffraction at GHz radio frequencies, x ~ 10¹⁰ cm (Cordes et al. 1985). For a Kolmogorov spectrum, they would be larger on larger scales in proportion to L^2/3; if the spectrum is continuous up to pc scales, the absolute fluctuation amplitude there would be ~ 1 (Lee & Jokipii 1976). Anisotropy of scattered images is at the level of 50%, which is consistent with extremely large intrinsic anisotropies ( × 1000) from MHD turbulence (sections 4.11 and 4.13 in Interstellar Turbulence I) if many orientations on the line of sight are blended together.