APPENDIX

RELAXATION TIME IN SPHEROIDS AND DISKS

A test particle moving at velocity v along a trajectory that passes a stationary field star of mass m with impact parameter b is deflected by the attraction of the field star. For a distant passage, it acquires a transverse velocity component |v| 2Gm / (bv) to first order (BT08 eq. 1.30). Encounters at impact parameters small enough to produce deflections where this approximation fails badly are negligibly rare and relaxation is driven by the cumulative effect of many small deflections.

If the density of field stars is n per unit volume, the test particle will encounter n = 2 b b nv stars per unit time with impact parameters between b and b + b. Assuming stars to have equal masses, each encounter at this impact parameter produces a randomly directed v that will cause a mean square net deflection per unit time of

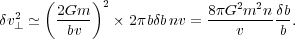(A1)

The total rate of deflection from all encounters is the integral over impact parameters, yielding

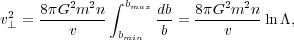(A2)

where ln ln(b_max / b_min) is the Coulomb logarithm. Typically one chooses the lower limit to be the impact parameter of a close encounter, b_min 2Gm / v², for which |v| is overestimated by the linear formula, while the upper limit is, say, the half-mass (or effective) radius, R, of the stellar distribution beyond which the density decreases rapidly. The vagueness of these definitions is not of great significance to an estimate of the overall rate because we need only the logarithm of their ratio. The Coulomb logarithm implies equal contributions to the integrated deflection rate from every decade in impact parameter simply because the diminishing gravitational influence of more distant stars is exactly balanced by their increasing numbers.

Note that the first order deflections that give rise to this steadily increasing random energy come at the expense of second order reductions in the forward motion of the same particles that we have neglected (Hénon 1973). Thus the system does indeed conserve energy, as it must.

We define the relaxation time to be the time needed for v² v², where v is the typical velocity of a star. Thus

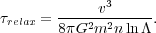(A3)

To order of magnitude, a typical velocity v² GNm / R, where N is the number of stars each of mean mass m, yielding N. Defining the dynamical time to be _dyn = R / v and setting N ~ R³ n, we have

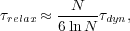(A4)

which shows that the collisionless approximation is well satisfied in galaxies, which have 10⁸ N 10¹¹ stars. Including the effect of a smooth dark matter component in this estimate would increase the typical velocity, v, thereby further lengthening the relaxation time.

This standard argument, however, assumed a pressure-supported quasi-spherical system in several places. Rybicki (1972) pointed out that the flattened geometry and organized streaming motion within disks affects the relaxation time in two important ways. First, the assumption that the typical encounter velocity is comparable to the orbital speed v = (GNm / R)^1/2 is clearly wrong; stars move past each other at the typical random speeds in the disk, say v with ~ 0.1, causing larger deflections and decreasing the relaxation time by a factor ³.

Second, the distribution of scatterers is not uniform in 3D, as was implicitly assumed in eq. (A1). Assuming a razor thin disk, changes the volume element from 2 v b b for 3D to 2v b in 2D, which changes the integrand in eq.& (A2) to b^-2 and replaces the Coulomb logarithm by the factor (b_min^-1 - b_max^-1). In 2D therefore, relaxation is dominated by close encounters. Real galaxy disks are neither razor thin, nor spherical, so the spherical dependence applies at ranges up to the typical disk thickness, z₀, beyond which the density of stars drops too quickly to make a significant further contribution to the relaxation rate. Thus we should use z₀ / b_min for disks. More significantly, the local mass density is also higher, so that N ~ R² z₀n. These considerations shorten the relaxation time by the factor (z₀ / R) ln(R / z₀). An additional effect of flattened distribution of scatterers is to determine the shape of the equilibrium velocity ellipsoid, as discussed in Section 10.3.

A third consideration for disks is that the mass distribution is much less smooth than is the case in the bulk of pressure supported galaxies. A galaxy disk generally contains massive star clusters and giant molecular clouds whose influence on the relaxation rate turns out to be non-negligible (see Section 10).