


Most of the behavior discussed so far, such as the non-linear evolution of instabilities, causes changes to the host galaxy on a dynamical time scale. The broad topic of secular evolution in galaxies describes changes that occur more gradually, such as the secular formation of pseudo-bulges (see Kormendy 1993, Kormendy & Kennicutt 2004 for excellent reviews, and also Kormendy's chapter in this volume), the formation of rings (e.g. Buta & Combes 1996), or dynamical friction between components (Section 9.8). The discussion in this section concerns processes that scatter disk stars only.
It has long been realized that old stars in the solar neighborhood have larger peculiar motions relative to the local standard of rest (hereafter LSR) than do young stars (e.g. Wielen 1977, Nordström et al. 2004, Aumer & Binney 2009); see also Freeman's chapter). Postulating that older stars were born with larger random speeds, say in a thicker disk, is unattractive because it makes the present epoch of low velocity dispersion special. Some mechanism to scatter stars must therefore be invoked to create the larger random speeds of older stars.
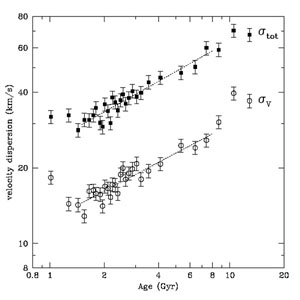
The trends presented in Fig. 16 use the revised ages (Holmberg et al. 2007) assigned to the GCS stars (see Soderblom 2010, for a review). Figs. 2, 3 & 4 of Aumer & Binney (2009) show the dispersions estimated as a function of color on the main sequence; while blue stars are necessarily young, red stars are expected to have a range of ages. The dispersions of the supposed oldest stars estimated by Holmberg et al. (2007) are no greater than those estimated by Aumer & Binney (2009) for their reddest stars, suggesting that the "older" bins in Fig. 16 include stars having a wide range of ages, as argued by Reid et al. (2007). It should be noted that the reported dispersions are simple second moments of the perhaps complex velocity distributions (see Fig. 1).
 |
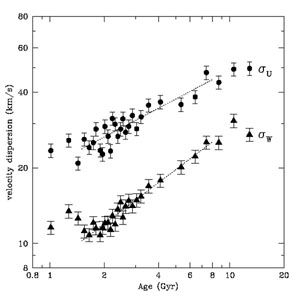 |
Figure 16. The dispersion of stars in all
three components, and the total dispersion of the GCS sample of solar
neighborhood stars using revised ages
(Holmberg et
al. 2007).
The radial, azimuthal and vertical components are
|
A reliable determination of the variation of dispersion as a function
of time could provide another useful constraint on the scattering
mechanism (e.g. BT08, Section 8.4).
Quillen & Garnett
(2000)
and
Seabroke & Gilmore
(2007)
argued that
the dispersion may saturate for stars above a certain age; with a much
older surge to account for the highest velocities. However,
Aumer & Binney
(2009)
found better fits to the data with continuous acceleration,
and deduced  ~
t0.35, with t being the current age of
the stellar generation, in tolerable agreement, in fact, with 0.38 for
the logarithmic slope of
~
t0.35, with t being the current age of
the stellar generation, in tolerable agreement, in fact, with 0.38 for
the logarithmic slope of
 tot in
Fig. 16.
tot in
Fig. 16.
Three principal scattering agents have been discussed: dense gas clumps in the disk, massive black holes in the halo, and recurrent short-lived spirals. Note that the first two are essentially collisional processes that accelerate the relaxation rate (see the Appendix), while the changescaused by spirals can increase random motion without leading to a more relaxed DF. As none in isolation fits the data, a combination of spirals and gas clumps seems to be favored. Minor mergers and the effects of halo substructure are discussed in Section 11.
An orbiting mass clump induces a collective spiral wake in the surrounding disk that enhances its mass and size by substantial factors (Julian & Toomre 1966), a complication that is ignored in many studies of cloud scattering. Since molecular gas is mostly concentrated in spiral arms (Nieten et al. 2006, Gratier et al. 2010, Efremov 2010, see also the chapter by Bania), it is probably futile to draw a sharp distinction between spiral arms and the wakes of dense gas clumps, and a correct treatment would be to calculate the effects of the combined star and gas disk. Binney & Lacey (1988) took a step in this direction, but a full calculation may remain unreachable for some time if one tries to include a self-consistent treatment of the formation and dispersal of the gas clumps: molecular gas concentrations probably grow in the converging gas flow into a spiral arm, and are subsequently dispersed by star formation.
Treating spirals and mass clumps in the disk as distinct scattering agents may be justified, therefore, if the wakes of cloud complexes can be lumped with spirals into a single scattering agent that is distinct from the clouds that caused them. At the very least, this simplifying assumption separates the problem into tractable pieces.
Lynden-Bell & Kalnajs (1972) showed that stars are scattered by a slowly changing potential perturbation only near resonances. More precisely, a spiral potential that grows and decays adiabatically, i.e. on a time-scale long compared with the orbital and epicyclic periods, will not cause a lasting change to a star's E and Lz. Wave-particle interactions become important near the resonances, where stars experience secular changes through "surfing" on the potential variations at CR or through a periodic forcing close to their epicyclic frequency at the Lindblad resonances. Either case produces a lasting change to a star's orbit.
The width of a resonance, i.e. the range of orbit frequencies of stars that are strongly affected, depends only on the amplitude of the potential when the perturbation is long-lived. But perturbations of shorter lifetimes have a broader range of frequencies and more stars experience lasting changes.
The discussion in Section 2.4 and Fig. 3 indicates that stars that lose (gain) Lz near the ILR (OLR) move onto more eccentric orbits, which is the root cause of heating by spirals. Exchanges at CR move stars to new orbits also, but with no change to the energy of non-circular motion, as discussed in Section 10.2.
Significant heating by spiral waves over a large part of a disk requires them to be transient; a quasi-steady pattern, of the type envisaged by Bertin & Lin (1996) say, will cause localized heating at an exposed resonance, while stars elsewhere will move through the pattern without otherwise being affected. Barbanis & Woltjer (1967), Carlberg & Sellwood (1985) and Binney & Lacey (1988) calculated the heating caused by transient spirals. Jenkins & Binney (1990), De Simone et al. (2004), and Minchev & Quillen (2006) presented numerical studies of the consequences for a disk of test particles subject to some assumed set of spiral wave perturbations.
It is important to realize that the vertical oscillations of stars are little affected by spiral potential variations (Section 2.6 and Carlberg 1987). In the absence of heavy clumps that can redirect disk velocities (Section 10.3), the increasing in-plane motions in simulations of initially cool, thin disks may ultimately cause the velocity ellipsoid to become sufficiently anisotropic as to cause it to thicken through mild buckling instabilities (Section 8.1). This may account for claims (e.g. McMillan & Dehnen 2007) that disks thicken due to spiral heating.
10.2. Churning by Transient Spirals
Studies of the metallicities and ages of nearby stars (Edvardsson et al. 1993, Nordström et al. 2004) found that older stars tend to have lower metallicities on average. As the ages of individual stars are disputed (Reid et al. 2007, Holmberg et al. 2007), the precise form of the relation is unclear. However, there seems to be general agreement that there is a spread of metallicities at each age, which is also supported by other studies (Chen et al. 2003, Haywood 2008, Stanghellini & Haywood 2010). The spread seems to be more than twice that expected from simple blurring of the gradient by stellar epicyclic excursions. In the absence of radial mixing, a metallicity spread amongst coeval stars is inconsistent with a simple chemical evolution model in which the metallicity of the disk rises monotonically in each annular bin.
Sellwood & Binney (2002) showed that scattering at CR causes very effective mixing. In a few Gyr, multiple transient spirals caused stars to diffuse in radius. Churning of the stellar disk occurs at corotation of the spirals with no associated heating, and is able to account for the apparent metallicity spread with age. Roskar et al. (2008ab) presented more detailed simulations that included infall, star formation and feedback that confirmed this behavior. Schön-rich & Binney (2009) developed the first chemical evolution model for the MW disk to include radial churning.
Many years before the discovery of giant molecular gas clouds,
Spitzer &
Schwarz-schild (1953)
postulated their existence to account for the secular heating of disk stars.
Lacey (1984)
extended their calculation to 3D
and concluded that cloud scattering should cause the vertical
dispersion,  z,
to be intermediate between the radial,
z,
to be intermediate between the radial,
 R, and azimuthal,
R, and azimuthal,

 ,
components.
16 This result seems
physically plausible on energy equipartition grounds: scattering by
massive clouds redirects the peculiar motions of stars through random
angles, and therefore isotropizes the motions as far as the epicycle
gyrations allow.
,
components.
16 This result seems
physically plausible on energy equipartition grounds: scattering by
massive clouds redirects the peculiar motions of stars through random
angles, and therefore isotropizes the motions as far as the epicycle
gyrations allow.
Despite the fact that redirecting peculiar motions happens much more
rapidly than they can be increased by the same scatterers, the data do
not reveal Lacey's expected axis ratio. The second moments of the
velocity distribution of solar neighborhood stars in the three
orthogonal directions (Fig. 16 and
Wielen 1977,
Aumer & Binney
2009)
satisfy the inequality
 z <
z <

 <
<
 R. The ratio
of the two in-plane components is in reasonable agreement with
expectations from epicyclic motions, but the vertical component is the
smallest, and this remains true for all groups when the stars are
subdivided according to color or estimates of their ages.
Gerssen et
al. (2000)
also observed a flattened ellipsoid in the disk of NGC 2895.
R. The ratio
of the two in-plane components is in reasonable agreement with
expectations from epicyclic motions, but the vertical component is the
smallest, and this remains true for all groups when the stars are
subdivided according to color or estimates of their ages.
Gerssen et
al. (2000)
also observed a flattened ellipsoid in the disk of NGC 2895.
Carlberg (1987) and Jenkins & Binney (1990) therefore developed the plausible argument that spirals drive up the in-plane components more rapidly than scattering is able to redirect those motions into the vertical direction, thereby accounting for the observed axis ratios of the velocity ellipsoid. Sellwood (2000) cited their argument as offering strong support for the transient spiral picture, but it now seems to be incorrect.
Ida et al. (1993) claimed that cloud scattering alone would lead to the vertical component being the smallest, with the precise axis ratio depending on the local slope of the rotation curve. Their simulations (Shiidsuke & Ida 1999), and others (e.g. Villumsen 1985, Hänninen & Flynn 2002), confirmed their expectation.
Sellwood (2008b)
resolved this disagreement using simulations of test
particles in the sheared sheet (see
Section 3.6). Scattering by
randomly distributed co-orbiting massclumps confirmed the
flattened velocity ellipsoid predicted by
Ida et al.
(1993).
Fig. 17 reveals why Ida's prediction differs
from Lacey's: Lacey, as others
(Spitzer &
Schwarz-schild 1953,
Binney & Lacey
1988),
assumed that cloud scattering is local, but the
ln term in the
formulae in the Appendix
implies that distant encounters dominate any scattering process in 3D,
at least to distances a few times the disk thickness. Distant
scatterers in the flattened geometry of a disk must predominantly
affect the in-plane star velocities, and couple much less strongly to
the vertical component. Fig. 17 shows the
equilibrium ratio
term in the
formulae in the Appendix
implies that distant encounters dominate any scattering process in 3D,
at least to distances a few times the disk thickness. Distant
scatterers in the flattened geometry of a disk must predominantly
affect the in-plane star velocities, and couple much less strongly to
the vertical component. Fig. 17 shows the
equilibrium ratio
 z /
z /
 R when
scatterers beyond the finite range
dmax artificially exert no forces. The ratio settles to
something close to Lacey's energy equipartition prediction when none
but the closest heavy clumps perturb the stars, but the equilibrium
ellipsoid flattens in separate experiments as more distant clouds are
included, tending towards Ida's result with no artificial cut off.
R when
scatterers beyond the finite range
dmax artificially exert no forces. The ratio settles to
something close to Lacey's energy equipartition prediction when none
but the closest heavy clumps perturb the stars, but the equilibrium
ellipsoid flattens in separate experiments as more distant clouds are
included, tending towards Ida's result with no artificial cut off.
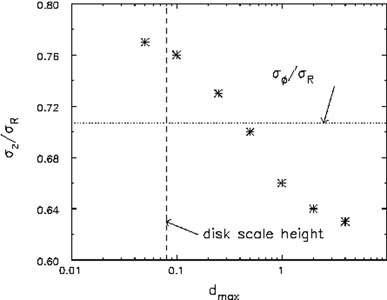 |
Figure 17. The equilibrium axis ratio of the velocity ellipsoid of particles plotted as a function of the limiting range of the perturbation forces from the heavy particles. See Sellwood (2008b) for a description of the calculations. |
Thus the shape of the local velocity ellipsoid, Fig. 16 is apparently consistent with cloud scattering, and does not require concurrent spiral arm scattering, as seemed attractive. However, the data do not imply that spirals are unimportant: cloud scattering seems unable to generate the random speeds of the oldest stars (e.g. Lacey 1991, Hänninen & Flynn 2002), and there are hints in Fig. 16 of some evolution of the velocity ellipsoid shape that may demand a compound origin.
The possibility that the dark matter halos of galaxies are made up of massive black holes (BHs) is not yet excluded. Lacey & Ostriker (1985) calculated the consequences for the stars in the disk of the MW, assuming the BHs to have orbits characteristic of a pressure-supported halo and to impart impulses to disk stars as they pass through the disk. The high speeds of their encounters with disk stars would cause the velocity dispersion to rise as t1/2, while the predicted shape of the velocity ellipsoid is in reasonable agreement with that observed.
Lacey & Ostriker
(1985)
addressed a number of issues with their model, such as the
X-ray accretion luminosity as the BHs pass through the gas disk, the
accumulation of BHs in the galactic center through dynamical
friction, and the survival of dwarf galaxies. They also acknowledged
that it does not predict the correct variation of
 tot
with Galactic radius. BT08 (Section 7.4.4) added that the idea could be
ruled out on the grounds that wide binary star systems would be
disrupted too quickly.
tot
with Galactic radius. BT08 (Section 7.4.4) added that the idea could be
ruled out on the grounds that wide binary star systems would be
disrupted too quickly.
If disk scattering is dominated by spirals, as argued below, then scattering by BHs would be needed merely to redirect the peculiar motions into the vertical direction. This reviewer is not aware of any such calculation, but since passing BHs scatter stars in the direction perpendicular to their orbits, it seems unlikely that they could redirect peculiar motion without also increasing in-plane motions. However, if this expectation is too pessimistic and the desired axis ratio could be achieved with lower BH masses, many of the other objections are weakened.
The extraordinary phase-space structure of the solar neighborhood (Dehnen 1998, Nordström et al. 2004 and Fig. 1) indicates that there is little in the way of an underlying smooth component and the stellar distribution is broken into several "streams" (Bovy et al. 2009). The features are too substantial to have simply arisen from groups of stars that were born with similar kinematics (e.g. Eggen 1996), as confirmed in detailed studies (Famaey et al. 2007, Bensby et al. 2007, Bovy & Hogg 2009).
Thus it is clear that the entire DF has been sculptured by dynamical processes. Were the large part of the spread in velocities caused by multiple scatterings off molecular clouds in the disk, or off black holes in the halo, the distribution should approximate the simple double Gaussian proposed by K. Schwarzschild (see BT08 Section 4.4.3). The vertical velocity distribution (Nordström et al. 2004), on the other hand, does have a relaxed appearance, as noted by Seabroke & Gilmore (2007).
Various dynamical agents have been proposed to account for kinematic features in the solar neighborhood. Kalnajs (1991) argued that the OLR of the bar in the MW might be close to the solar circle. Features in the subsequently-released HIPPARCOS data have also been attributed to the OLR of the bar (Raboud et al. 1998, Dehnen 2000, Fux 2001), while Sellwood (2010) attributed another to a recent ILR.
De Simone et al. (2004) were able to produce distributions of stars with a similar degree of substructure in simulations of test particles moving in the adopted potential perturbations representing a succession of short-lived spiral transients; see also Minchev & Quillen (2006). Other models that included both bars and spirals were presented by Quillen (2003), Chakrabarty (2007), and Antoja et al. (2009), while Helmi et al. (2006) suggested that some of the substructure may also be caused by satellite infall (see also Section 11).
Since spirals (and bars) are inefficient at exciting vertical motions, another scattering process needs to be invoked to redirect in-plane random motion into vertical motion. The influence of clumps in the disk, which are known to exist, seems consistent with the relaxed appearance of the vertical velocity distribution. Furthermore, the observed axes of the velocity ellipsoid, except possibly for the youngest stars (Fig. 16), are consistent with the prediction of cloud scattering. Thus cloud scattering seems to be just sufficient to redirect velocities, which they are good at, but not to contribute significantly to heating.
16 The ratio
 R /
R /


 2
2 /
/
 (BT08, eq. 8.117)
is forced by epicyclic motions of disk stars.
Back.
(BT08, eq. 8.117)
is forced by epicyclic motions of disk stars.
Back.