4.3. ORBITS AND RESONANCES

Before starting on our quest for understanding the main bar formation and evolution processes, let me first give a brief and considerably simplified description of some basic notions of orbital structure theory. Readers interested in more thorough and rigorous treatments can consult Arnold (1989) and Lichtenberg & Lieberman (1992).

Let me consider a very simple potential composed of an axisymmetric part (including all axisymmetric components) and a rigid bar rotating with a constant angular velocity _p. It is in general more convenient to work in a frame of reference which co-rotates with the bar, in order to have a time-independent potential (Binney & Tremaine 2008) and I will simplify things further by restricting myself to 2D motions. Any regular galactic orbit in this potential ⁴ can be characterised by two fundamental frequencies, _i, i = 1,2. In the epicyclic approximation these are , the angular frequency of rotation around the galactic centre, and , the epicyclic frequency, i.e., the frequency of radial oscillations. We say that an orbit is resonant if there are two integers l and m such that

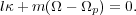(4.1)

The most important resonances for our discussions here will be the Lindblad resonances (inner and outer) and the corotation resonance. The inner Lindblad resonance (hereafter ILR) occurs for l = -1 and m = 2. Therefore, in a frame of reference co-rotating with the bar, such orbits will close after one revolution around the centre and two radial oscillations (Fig. 4.2).

Figure 4.2. Examples of epicyclic orbits. Left panel: A non-resonant orbit. Central panel: Orbit at inner Lindblad resonance, i.e., for (l, m) = (-1,2). Right panel: Orbit at corotation resonance, i.e., for l = 0. In all three panels, the dashed line gives the circular (guiding) orbit.

Contrary to regular orbits, chaotic orbits (often also called irregular orbits) do not have two fundamental frequencies and this property can be used to distinguish them from regular orbits with the help of what is often called a frequency analysis (Binney & Spergel 1982; Laskar 1990). Let us also briefly mention the so-called sticky orbits. Information on the dynamics and properties of such orbits can be found in Contopoulos (2002). Here we will only mention that, classified by eye, such orbits can be seen as being, say, regular over a given interval of time and then, within a relatively short time, turning to chaotic. Not too many years ago the existence and effect of non-regular orbits on the structure and dynamics of galaxies was generally neglected, but it is becoming progressively clear that this was wrong, so that such orbits are now known to play a considerable role in many fields of galactic dynamics.

By definition, resonant orbits close after a certain number of revolutions and a certain number (not necessarily the same) of radial oscillations, and are often referred to as periodic orbits. Several studies of such orbits in various bar potentials have been made in 2D cases ⁵ (e.g., Contopoulos & Papayannopoulos 1980; Athanassoula et al. 1983; Contopoulos & Grosbøl 1989). They show that, in the equatorial plane, the main supporters of the bar are a family of orbits elongated along the bar, named x₁ and having l = -1 and m = 2. Examples of members of this family can be seen in Fig. 4.3 here, or in Fig. 7 of Contopoulos & Papayannopoulos (1980), or Fig. 2 of Skokos et al. (2002a). In most cases there is another family of orbits with l = -1 and m = 2, but which are oriented perpendicularly to the bar and are named x₂. These play a crucial role in determining the gas flow in the bar and the morphology of the inner kpc region in the centre of the galaxy and will be discussed further by Isaac Shlosman (this volume). Finally there are also two main families of periodic orbits at CR, examples of which can be seen, e.g., in Fig. 3 and 4 of Contopoulos & Papayannopoulos (1980).

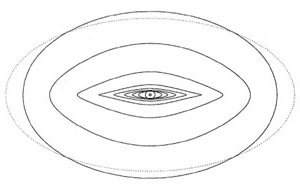Figure 4.3. Examples of orbits of the x1 family. The outline of the bar is given by a dashed line (reproduced from Athanassoula 1992a).

Periodic orbits can be stable or unstable and this can be tested by considering another orbit very near the periodic one in phase space, i.e., with very similar values of positions and velocities. If the periodic orbit is stable, then the new orbit will stay in the immediate surroundings of the periodic one and `wrap' itself around it. It can then be said that this new orbit is `trapped' by the periodic one. Examples of trapped orbits can be seen in Fig. 3.19 of Binney & Tremaine (2008). The bar can then be considered as a superposition of such orbits, trapped around members of the x₁ family, which will thus be the backbone of the bar. On the other hand, if the periodic orbit is unstable, then this second orbit will leave the vicinity of the periodic orbit, and the distance between the two orbits in phase space will increase with time, even though initially they were very near.

The calculation of periodic orbits is straightforward, yet such orbits can reveal crucial information on galactic structure and dynamics. A good example is the work of Contopoulos (1980), who, with simple considerations on closed orbits, was able to show that bars cannot extend beyond their CR. Further work on periodic orbits coupled to hydrodynamic simulations gave an estimate of the lower limit to the bar length, and the ratio of the corotation radius to the bar length was found to be in the range of 1.2 ± 0.2 (Athanassoula 1992a, 1992b). Note, however, that the lower limit is only an estimate, and not a strict limit as the upper limit. Nevertheless, several other methods and works, including observational, gave results within the above-quoted range, as reviewed by Elmegreen (1996) and by Corsini (2011). The bars for which 1.0 < < 1.4 are called fast, contrary to bars with > 1.4, which are called slow.

Finally, a straightforward superposition (with some smoothing) of stable periodic orbits offers a very simple, yet most useful tool for studying morphological or kinematical structures in disk galaxies and has been successfully applied to bars, box/peanuts and rings (e.g., Patsis et al. 1997; Bureau & Athanassoula 1999; Patsis et al. 2002, 2003; Patsis 2005; Patsis et al. 2010).

⁴ A number of concepts and results discussed in this section are much more general, and can be applied to a more general class of potentials. Back

⁵ 3D cases will be discussed in Section 4.8.2. Back