


4.8.1. Peanuts: input from simulations, orbits and observations
When bars form in N-body simulations they have a thin vertical density profile, similar to that of the disk. In other words, it is the in-plane rearrangement of the disk material that creates the bar, when initially near-planar and near-circular orbits become more elongated and material gets trapped around the stable periodic orbits of the x1 family, as already discussed in Section 4.3 and 4.6.4. This configuration, however, lasts for only a short while, after which the bar buckles out of the plane and becomes asymmetric with respect to the equatorial plane, as shown, e.g., in Combes et al. (1990) and Raha et al. (1991), and as is illustrated in the middle central panel of Fig. 4.1. This evolutionary phase, which can be called the asymmetry phase, is also very short-lived and soon the side-on view displays a clear peanut or boxy shape. During the peanut formation phase the strength of the bar decreases considerably (Combes et al. 1990; Raha et al. 1991; Debattista et al. 2004, 2006; Martínez-Valpuesta & Shlosman 2004; Martínez-Valpuesta et al. 2006; Athanassoula 2008a). Two examples of this decrease can be seen in Fig. 4.9, one for an MH-type simulation (where the bar strength decrease starts only at roughly 6 Gyrs) and another for an MD-type simulation (where it already starts at roughly 3 Gyrs). This decrease can sometimes be very important, so that it could get erroneously interpreted as a bar destruction.
These boxy/peanut structures had been observed in real galaxies many times, well before being seen in simulations. Due to the fact that they extend vertically well outside the disk, they were called bulges. More specifically, if they have a rectangular-like (box-like) outline they are called boxy bulges, and if their outline is more reminiscent of a peanut, they are called peanut bulges. Sometimes, however, this distinction is not made and the words `boxes' or `peanuts' are used indiscriminately, or the more generic term `boxy/peanut' is used instead. A number of kinematical or photometrical observations followed and comparisons of their results with orbits and with simulations established the link of boxy/peanut bulges to bars (Kuijken & Merrifield 1995; Athanassoula & Bureau 1999; Bureau & Athanassoula 1999; Bureau & Freeman 1999; Merrifield & Kuijken 1999; Lütticke et al. 2000; Aronica et al. 2003; Chung & Bureau 2004; Athanassoula 2005b; Bureau & Athanassoula 2005; Bureau et al. 2006).
4.8.2. Peanut-related orbital structure
Considerable information on boxy/peanut structures can be obtained with the help of orbital structure theory. In 3D the orbital structure is much more complex than in 2D, as expected. Thus, the x1 family has many sections (i.e., energy ranges) where its members are vertically unstable, and, at the energies where there is a transition from stability to instability, a 3D family can bifurcate (i.e., emerge). The orbits that are trapped around the stable l = 1, m = 2, n ≠ 0 periodic orbits of this family can participate in the boxy/peanut structure (Patsis et al. 2003). They were discussed by Pfenniger (1984) and by Skokos et al. (2002a, b), who presented and described a number of relevant families. Since these orbits bifurcate from the x1 and create vertically extended structures, they were named by Skokos et al. (2002a) by adding a vi, i = 1, 2, ... after the x1, i.e., x1 vi, i = 1, 2, ..., where i is the order of the bifurcation. Projected on the (x, y) plane, their shape is very similar to that of the members of the planar x1 family. Good examples of such periodic orbits can be seen in Fig. 9 of Pfenniger (1984), or Fig. 7 to 10 of Skokos et al. (2002a).
4.8.3. Peanuts as parts of bars: shape and extent
Contrary to what has been very often said and written, boxy/peanut bulges are not bars seen edge-on. The correct statement is that boxy/peanut bulges are the inner parts of bars seen edge-on. The evidence for this was put together and discussed in Athanassoula (2005b) and I will only summarise it briefly here. Orbital structure theory shows that not all planar periodic orbits of the x1 family are vertically unstable. In fact, the ones in the outer part of the bar are stable. Therefore, the outer part of the bar will stay thin and only the part within a given radius will thicken, so that the peanut will be shorter than the bar. This gives the bar an interesting form. As a very rough approximation, one can think of the bar as a rectangular parallelepiped box (like a shoe box), from the two smallest sides of which (perpendicular to the bar major axis) stick out thin extensions. Of course this is a very rough picture and the shape of the `box' is in fact much more complex than a rectangular parallelepiped, while the extensions have shapes which are difficult to describe. The best is to look at an animation 7 where one can see a bar from a simulation, from various viewing angles.
How much longer is the bar than the peanut? The answer to this question is not unique and depends on which one of the x1 vi families sets the end of the peanut, on the galactic potential and on the bar pattern speed (Patsis et al. 2003).
Figure 4.13 gives an estimate of the ratio of boxy/peanut to thin bar length, for one of my simulations. In general, it is much easier to obtain an estimate of this ratio for simulations than for observed galaxies, because one can view snapshots from any desired angle. Thus, the length of the bar can be obtained from the face-on view (lower panel) as the major axis of the largest isophotal contour that has a bar shape. This of course introduces an uncertainty of a few to several percent, but is about as good as one can achieve with difficult quantities such as the bar length 8. The size of the boxy/peanut part can be found from the edge-on view (upper panel). This also introduces an uncertainty, probably much larger than that of the bar length (AM02), but even so one can get reasonable estimates of the ratio of the two extents, and certainly make clear that the thin part of the bar can be much longer than the thick boxy/peanut part. Further discussion of this, and further examples can be found in Athanassoula (2005b), Athanassoula & Beaton (2006) and Athanassoula (2008a).
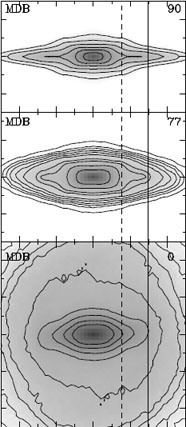 |
Figure 4.13. Three views of the baryonic components (disk and bulge) of a simulation. For each panel the inclination angle is given in the upper right corner, the value of 77 degrees corresponding to the inclination of the Andromeda galaxy (M 31). The solid vertical line gives an estimate of the bar length from the face-on view, while the dashed vertical line gives an estimate of the length of the boxy/peanut structure, as obtained from the side-on view. |
Estimates of the ratio of boxy/peanut to thin bar length can also be obtained from observations. Nevertheless, information for observed galaxies can be obtained from only one viewing angle and these estimates are less precise than the corresponding simulation ones. Figure 4.14 allows us to get an estimate for NGC 2654. Lütticke et al. (2000) made a cut along the major axis of this edge-on disk galaxy and from the projected surface density profile along it they obtained the thin bar length (confront with method (vi) from AM02). They also made cuts parallel to this and offset above or below it and from them could obtain the extent of the bar/peanut part. In this way, Lütticke et al. (2000) were able to measure the ratio of extent of the thin part of the bar to the extent of the thick boxy/peanut part and show clearly that the former can be much longer than the latter.
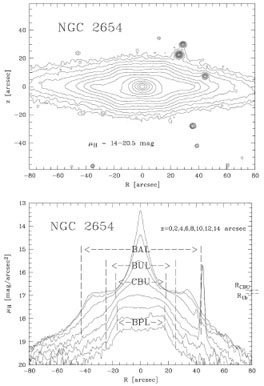 |
Figure 4.14. Upper panel: Isophotes for the edge-on disk galaxy NGC 2654 in the near-infrared. Lower panel: Surface brightness profiles from cuts along, or parallel to the major axis of this edge-on disk galaxy. From the cut along the major axis (uppermost curve), it is possible to obtain an estimate of the projected bar length - BAL on the plot. The size of the boxy/peanut bulge is obtained from cuts parallel to the major axis, but offset from it above or below the equatorial plane - BPL on the plot. (Figure 1 of Lütticke et al. 2000, reproduced with permission © ESO). |
4.8.4. The boxy/peanut system in the Milky Way
The bar shape described in the previous section has important implications for the structure of the Milky Way. It is now well established that our Galaxy is barred (e.g., de Vaucouleurs 1964; Binney et al. 1991; Blitz & Spergel 1991). The thick component which can be seen to extend outside the Galactic plane in the near-infrared COBE (COsmic Background Explorer) image is often referred to as the COBE / DIRBE (Diffuse Infrared Background Experiment) bar, or the thick bar. About ten years later, further evidence started accumulating and was initially interpreted as due to the existence of a second bar, longer than the first one and considerably thinner (Hammersley et al. 2000; Benjamin et al. 2005; Cabrera-Lavers et al. 2007; López-Corredoira et al. 2007; Cabrera-Lavers et al. 2008; Churchwell et al. 2009). This second bar has been named the Long bar. The existence of a second bar is very common in barred galaxies and about a fourth or a fifth of disk galaxies have both a primary or main bar and a secondary or inner bar (Erwin & Sparke 2002; Laine et al. 2002; Erwin 2011). However, the ratio of the lengths of the two presumed Milky Way bars is totally incompatible with what is observed in double-barred external galaxies (Romero-Gómez et al. 2011), and it would be very dangerous to assume that our Galaxy has morphological characteristics so different from those of external galaxies.
There are two very important clues that can help us understand the nature of the bar system in the Milky Way. The first one is that the COBE / DIRBE bar is thick while the Long bar is thin, their ratio of minor (z-) axis to major axis being of the order of 0.3 and 0.03, respectively. The second one is that the COBE / DIRBE bar is shorter than the Long bar by a factor of roughly 0.8. These clues, taken together with the discussion in Sections 4.8.2 and 4.8.3, point clearly to a solution where the thick COBE / DIRBE bar and the thin bar are just parts of the same single bar, the former being its thick boxy/peanut part and the latter being its outer thin part. This alternative was first proposed for our Galaxy by Athanassoula (2006, 2008b) and first tested by Cabrera-Lavers et al. (2007) using their red-clump giant measurements. This suggestion was disputed at the time, because a number of observations (Hammersley et al. 2000; Benjamin et al. 2005; Cabrera-Lavers et al. 2008) argued that the position angles of the COBE / DIRBE bar and of the Long bar are considerably different, with values between 15 and 30 degrees for the former and around 43 degrees for the latter.
Yet this difference in orientations is not a very strong argument. First, due to our location within the Galaxy, the estimates for the Galactic bar position angles are much less accurate than the corresponding estimates for external galaxies. Thus, Zasowski et al. (2012) find the position angle of the Long bar to be around 35 degrees, i.e., much closer to that of the COBE / DIRBE bar than the 43 degrees estimated in previous works. Second, if the shape of the outer isodensity contours of the thin part of the bar are, in the equatorial plane, more rectangular-like than elliptical-like - as is often the case in external galaxies (e.g., Athanassoula et al. 1990; Gadotti 2008, 2011) - the Long bar position angle will appear to be larger than what it actually is. A third is that our Galaxy could well have an inner ring, of the size of the bar. N-body simulations have shown that, in such cases, there is often within the ring a short, leading segment near the end of the bar. Examples can be found in Fig. 2 in AM02, Fig. 3 and 12 in A03, Fig. 2 in Romero-Gómez et al. (2011), or Fig. 1 in Martínez-Valpuesta & Gerhard (2011). Such a segment can spuriously increase the observed position angle of the Long bar.
In view of all the above comments, the small difference between the position angle of the COBE / DIRBE bar and that of the Long bar should not be a major concern. I thus still believe that my initial proposal, that the COBE / DIRBE and the Long bar are parts of the same bar, is correct.
7 http://lam.oamp.fr/recherche-14/dynamique-des-galaxies/scientific-results/milky-way/bar-bulge/how-many-bars-in-mw, or in http://195.221.212.246:4780/dynam/movie/MWbar. Back.
8 A discussion of the various methods that can be used to measure a bar length in simulations, in ensembles of orbits and/or in observations, and of their respective advantages and disadvantages can be be found in AM02, Patsis et al. (2002), Michel-Dansac & Wozniak (2006) and Gadotti et al. (2007). Back.