Copyright © 2009 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2009. 47:
159-210 Copyright © 2009 by Annual Reviews. All rights reserved |
5.1. General description and identification
Elliptical galaxies are recognizable by their smooth, symmetric, and deceptively simple-looking appearance. Figure 13 shows some typical elliptical galaxies drawn from the SDSS, using the classifications reported by NED. In this case, we had to reject about one-third of the classifications as obviously incorrect. Figure 12 shows the distribution of their broad-band properties along with the S0s. They are concentrated, uniformly red, and follow a reasonably tight size-luminosity relation.
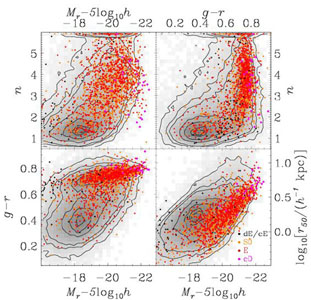 |
Figure 12. Distribution of elliptical and lenticular galaxy types in optical broadband properties. Similar to Figure 8, but now showing S0 galaxies (orange), E galaxies (red), dE galaxies (black) and cD galaxies (magenta). |
The past two decades of research, however, have revealed the complexity of their dynamical structure, their star-formation history, and their assembly history. In general terms they are dynamically supported by velocity dispersion, but often with significant rotational support as well. Their stellar populations are old, ongoing star-formation is rare, and their cold gas content is low (around or less than 1%). However, there are numerous indications that at least some ellipticals were assembled late, after the hey-day of their star-formation. In addition, the small amount of star-formation that does occur in ellipticals seems to be similar in nature to that in spirals: molecular clouds in gas disks forming stars, at the same (low) efficiency found in spirals.
Among luminous ellipticals there are two discernible classes, those with and without cores (Section 5.3; Kormendy et al. 2009 and references therein). The ellipticals with nuclear cores, relative to those without, tend to be more luminous, have b / a closer to unity, have boxier isophotes, less rotational support, and more signs of triaxiality.
Among lower luminosity ellipticals there are at least three classes: low surface brightness, exponential galaxies typed as dE or sometimes Sph (such as NGC 205); high surface brightness, concentrated galaxies usually typed as cE (such as M32); and ultra-compact dwarfs with r50 as small as 10 pc (Drinkwater et al. 2004). Kormendy et al. (2009) reviews the distinction between the first two classes, arguing that the cE population is most similar to the giant elliptical population. Ferrarese et al. (2006) presents the alternative argument for dE galaxies.
Relative to S0s, the surface brightness profiles of ellipticals appear to have no "edge," as S0s do. However, in their other properties - sizes, profile shapes, colors, symmetry, and smoothness - Es and S0s are very similar. Thus, the recent literature on very large samples is plagued with "elliptical" or "early-type" samples that actually include a fair number of S0s as well as early-type or edge-on spirals. Interestingly, these interlopers do not appear to affect many of the scaling relations we discuss here; nevertheless, they can be important in some circumstances and we emphasize again the importance of separating these two populations.
Although many astrophysicists typically think of ellipticals as de Vaucouleurs profile galaxies, in fact they have a range of Sérsic indices, whose values depend rather strongly on luminosity (as has been recognized for a long time; Caon, Capaccioli & D'Onofrio 1993, Prugniel & Simien 1997). The first row of Figure 6 shows this distribution, which reveals that selecting ellipticals using a strict cut in Sérsic index will exclude a significant (and luminosity-dependent) fraction of viable elliptical galaxy candidates. Kormendy et al. (2009) demonstrate this trend most clearly with a careful analysis of elliptical surface brightness profiles.
These structural trends are mostly independent of environment, as Figure 6 shows (Blanton et al. 2005a, Park et al. 2007). With the exception of the most luminous cases, red galaxies of a given luminosity are no more or less likely to be concentrated when they are found in dense regions. This result suggests that any process that turns spiral galaxies into ellipticals acts similarly in dense and underdense regions.
One shortcoming of the 2D Sérsic profile is that when examined
carefully few ellipticals actually have precisely elliptical
isophotes. One way of quantifying this non-ellipticity is to consider
the residuals of the actual isophotes relative to perfect ellipses.
If one Fourier transforms these residuals, the
cos4 term is
of order 1% of the isophotal radius for many ellipticals
(Bender &
Moellenhoff 1987).
The fractional amplitude of this term a4 / a
is defined such that positive values are "diskier" than ellipses
while negative values are "boxier." Generally, boxy galaxies are
more luminous than disky galaxies and more likely to exhibit a core (e.g.,
Kormendy &
Djorgovski 1989;
also see Section 5.4).
term is
of order 1% of the isophotal radius for many ellipticals
(Bender &
Moellenhoff 1987).
The fractional amplitude of this term a4 / a
is defined such that positive values are "diskier" than ellipses
while negative values are "boxier." Generally, boxy galaxies are
more luminous than disky galaxies and more likely to exhibit a core (e.g.,
Kormendy &
Djorgovski 1989;
also see Section 5.4).
The structure of the central regions of ellipticals are now observable
for large samples using HST imaging
(Ferrarese et
al. 2006,
Lauer et al. 2007a;
see in particular the review of
Kormendy
et al. 2009).
Although these analyses have varied in
their details, they all find that the central stellar mass surface
density profiles can reasonably be modeled as a power law
 (r)
(r)
 r-
r- . As defined by
Lauer et
al. (1995),
galaxies with
. As defined by
Lauer et
al. (1995),
galaxies with
 ~ 0.0-0.3 are classified as "cores," and galaxies with
~ 0.0-0.3 are classified as "cores," and galaxies with
 ~
0.5-1.0 are classified as "cusps," or sometimes
"power-law," "extra-light," or just "coreless." There are of
course galaxies in between the extremes
(Rest et al. 2001).
~
0.5-1.0 are classified as "cusps," or sometimes
"power-law," "extra-light," or just "coreless." There are of
course galaxies in between the extremes
(Rest et al. 2001).
The ellipticals with cores are the most luminous galaxies, with MV - 5log10 h < -21, and correspondingly have distinctly higher global Sérsic indices, boxier isophotes, slower rotation, and more triaxiality (Ferrarese et al. 2006, Lauer et al. 2007a, Kormendy et al. 2009). An oft-used model for the shapes of elliptical galaxy cores is the "Nuker" model introduced by Lauer et al. (1995), which is close to a broken power law. This model does not accurately reflect the surface brightness profiles of ellipticals at galactic radii larger than r50, which tend to be closer to Sérsic profiles. Consequently, several researchers (e.g., Kormendy 1999, Trujillo et al. 2004, Ferrarese et al. 2006) have suggested the use of a Sérsic model altered to transition to a power law near the center. These cores are thought to be scoured by the gravitational effects of binary black holes during mergers (for a review see Kormendy et al. 2009).
For -21 < MV - 5log10 h < -18, ellipticals tend to be cuspy (Ferrarese et al. 2006). Relative to the Sérsic models, these coreless galaxies often actually have an "extra light" component. The central light typically has isophotes that deviate from ellipses, being "diskier" (a4 / a > 0). If cuspy elliptical galaxies form in mergers, the diskiness of the central light components suggest that the last of these mergers should have been "wet," with dissipative processes triggering star-formation and raising the central stellar surface density, and swamping the effects of black hole scouring (Kormendy et al. 2009).
5.4. Fundamental plane and dynamics
The SDSS survey has provided an unprecedented sample of galaxies with
reliable spectroscopic velocity dispersions, allowing a detailed
analysis of the fundamental plane (FP;
Djorgovski
& Davis 1987,
Faber et
al. 1987)
- the tight relationship among r50,
half-light surface brightness I50, and velocity dispersion
 .
Bernardi et
al. (2007)
selected nearby early-types according to concentration, color and
emission line strength and found that for a relationship like
r50
.
Bernardi et
al. (2007)
selected nearby early-types according to concentration, color and
emission line strength and found that for a relationship like
r50 

 I50
I50 , the best fit is
(
, the best fit is
( ~ 1.3,
~ 1.3,
 ~ -0.76),
in only mild disagreement with the previous findings of
Jørgensen,
Franx & Kjaergaard (1996)
based on more local samples
(
~ -0.76),
in only mild disagreement with the previous findings of
Jørgensen,
Franx & Kjaergaard (1996)
based on more local samples
( ~ 1.25,
~ 1.25,
 ~ -0.82).
~ -0.82).
The FP differs from a naïve prediction based on the virial
theorem. From dimensional analysis,
M = c
 2R /
G, where
c is a structural constant that depends on the orbital structure,
the mass density profile, the surface brightness profile, and an
appropriately weighted mass-to-light ratio, R is a characteristic
radius, and G is the gravitational constant. Indeed, the rotation
of these parameters into the
2R /
G, where
c is a structural constant that depends on the orbital structure,
the mass density profile, the surface brightness profile, and an
appropriately weighted mass-to-light ratio, R is a characteristic
radius, and G is the gravitational constant. Indeed, the rotation
of these parameters into the
 -space of
Bender, Burstein
& Faber (1992)
was motivated by this virial interpretation. In this case, for a constant
mass-to-light ratio the FP parameters become
(
-space of
Bender, Burstein
& Faber (1992)
was motivated by this virial interpretation. In this case, for a constant
mass-to-light ratio the FP parameters become
( = 2,
= 2,
 = -1),
rather different than the observed ones. Several possible explanations
exist for the deviation from this relation: (a) a variation of the
stellar mass to dynamical mass ratio; (b) a variation of the stellar
mass-to-light ratio; or (c) "non-homology," that is, a variation in
the nature of ellipticals that changes c. Most analyses now favor
the first explanation, with a dynamical to stellar mass
ratio that scales as (CREN PUT THIS EQUATION IN)
= -1),
rather different than the observed ones. Several possible explanations
exist for the deviation from this relation: (a) a variation of the
stellar mass to dynamical mass ratio; (b) a variation of the stellar
mass-to-light ratio; or (c) "non-homology," that is, a variation in
the nature of ellipticals that changes c. Most analyses now favor
the first explanation, with a dynamical to stellar mass
ratio that scales as (CREN PUT THIS EQUATION IN)
First, spectral synthesis modeling suggests that very little of that variation can be attributed to the stellar mass-to-light ratio (Padmanabhan et al. 2004, Bernardi et al. 2006, Trujillo, Burkert & Bell 2004, Proctor et al. 2008). Second, detailed modeling of the 2D dynamics using integral field measurements generally finds a variation of Mdyn / M∗ that is quantitatively similar to the virial estimates that assume homology (Cappellari et al. 2006, Thomas et al. 2007). Third, direct constraints on mass density profiles with strong gravitational lensing indicate that the dynamical mass to light ratio is changing (Bolton et al. 2008).
Nevertheless, as Cappellari et al. (2006) notes, it is curious that the simple virial estimate yields the same mass-to-light ratio trends as more complex and direct modelling. After all, the assumptions of homology must be wrong in detail, as Trujillo et al. 2004 point out. Cappellari et al. (2006) further caution that the virial estimate only works if the de Vaucouleurs estimate of r50 is used - notwithstanding the fact that the de Vaucouleurs model is incorrect for many of these galaxies!
The FP is a weak function of environment, as with all other scaling relationships. For example, Park et al. (2007) shows that the Faber-Jackson relationship does not vary significantly. The FP analysis of Bernardi et al. (2006) detected a 0.1 mag surface brightness shift between the highest and lowest density subsamples, which they estimated was consistent with an age difference of 1 Gyr between cluster and field ellipticals (see Section 5.7).
The apparent simplicity of the FP relationship masks a good deal of variability and complexity in elliptical dynamics. For example, ellipticals are known to occasionally contain multiple kinematically distinct components (Efstathiou, Ellis & Carter 1982), often in the form of rotating disks around the core (Bender 1988). In addition, the kinematics is often misaligned with the photometry or twists as a function of radius, often interpreted as a sign of triaxiality (e.g., Binney 1978, Schechter & Gunn 1979). The recent analysis of SAURON data has greatly increased our understanding of the variety and incidence of kinematic substructures and other features (e.g., Krajnovic et al. 2008).
The FP also masks the importance of rotation to the global dynamics of
many ellipticals. Traditionally, this importance has been quantified
by the ratio of rotation speed to central velocity dispersion,
V/ (originally due to
Illingworth
1977,
but see the latest discussion of
Binney 2005).
Using SAURON data,
Cappellari et
al. 2007
argue for a different estimator
(originally due to
Illingworth
1977,
but see the latest discussion of
Binney 2005).
Using SAURON data,
Cappellari et
al. 2007
argue for a different estimator
 r =
<R|V|> / <R (V2 +
r =
<R|V|> / <R (V2 +
 2)1/2>, where the averages are
weighted by
flux. This measurement requires 2D velocity maps but is apparently a
better tracer of the angular momentum content than
V /
2)1/2>, where the averages are
weighted by
flux. This measurement requires 2D velocity maps but is apparently a
better tracer of the angular momentum content than
V /  , which is
more significantly affected by
kinematically decoupled cores as well as projection effects.
, which is
more significantly affected by
kinematically decoupled cores as well as projection effects.
Figure 14 shows the distribution of
 r from
Emsellem et
al. (2007),
for the SAURON sample of Es and S0s.
The upper left panel shows the relationship between angular momentum
content and virial mass Mvir. The red points are the
"slow rotators" according to the SAURON definition
(
r from
Emsellem et
al. (2007),
for the SAURON sample of Es and S0s.
The upper left panel shows the relationship between angular momentum
content and virial mass Mvir. The red points are the
"slow rotators" according to the SAURON definition
( r <
0.1). For comparison, in the bottom two
panels we also show the distribution of the isophotal shape parameter
a4 / a
(Section 5.2) as a function of both
Mvir and
r <
0.1). For comparison, in the bottom two
panels we also show the distribution of the isophotal shape parameter
a4 / a
(Section 5.2) as a function of both
Mvir and
 r. The
upper right panel of Figure 14 shows
r. The
upper right panel of Figure 14 shows
 r versus
the observed ellipticity
r versus
the observed ellipticity
 within
r50. Overplotted is the approximate curve for an
oblate rotator with an isotropic velocity dispersion, seen edge-on.
within
r50. Overplotted is the approximate curve for an
oblate rotator with an isotropic velocity dispersion, seen edge-on.
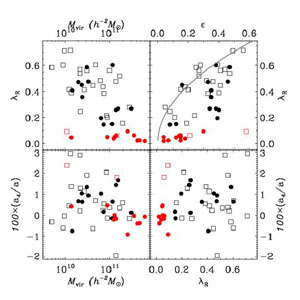 |
Figure 14. Distribution of E/S0 galaxy
properties from the SAURON sample of
Emsellem et
al. (2007).
Black symbols indicate
"fast rotators," while red points indicate "slow rotators".
Filled points indicate optically classified elliptical galaxies, while
open square symbols indicate S0s. Mvir indicates the
virial mass;
|
The most massive systems have a strong tendency to be the slowest
rotators, the closest to perfect ellipsoids, and the most
axisymmetric. Relative to the "fast rotators," these slow rotators
tend to have higher masses, flat or falling
 r
profiles, less cuspy centers (Section 5.2), more boxy
isophotes, more
kinematically decoupled cores, and greater kinematic misalignments
(indicating triaxiality). It is difficult to tell with the available
data whether there are some independent relationships among these
properties that are responsible for the others. However, the overall
trend is suggestive of the importance of major dry mergers in the
formation of these systems (e.g.,
Hernquist
1993),
but perhaps not minor dry mergers
(Burkert et
al. 2008).
r
profiles, less cuspy centers (Section 5.2), more boxy
isophotes, more
kinematically decoupled cores, and greater kinematic misalignments
(indicating triaxiality). It is difficult to tell with the available
data whether there are some independent relationships among these
properties that are responsible for the others. However, the overall
trend is suggestive of the importance of major dry mergers in the
formation of these systems (e.g.,
Hernquist
1993),
but perhaps not minor dry mergers
(Burkert et
al. 2008).
The lower mass systems have a stronger tendency to be "disky" and
are faster rotators. They tend to have disky isophotes as well as
aligned kinematics and photometry without twists (consistent with the
importance of rotation;
Cappellari et
al. 2007).
Detailed analysis of
their 2D dynamics suggests that they tend to have anisotropic velocity
dispersions, as their positions in the upper right panel of
Figure 14 suggests
(Cappellari et
al. 2007).
Interestingly, the
S0s, while always fast rotators, do not appear to be particularly
distinct from fast rotator ellipticals in their dynamics (though the
SAURON analysis is limited to radii
 r50).
r50).
Thus, though the FP is simple and appears to remain relatively constant
with environment, there are still only small samples available with
truly detailed 2D dynamics
( 100 nearby
ellipticals total).
Thus, nobody has explored whether these more detailed properties vary
with environment even as the FP remains relatively constant; such a
detection would be an important constraint on formation mechanisms.
100 nearby
ellipticals total).
Thus, nobody has explored whether these more detailed properties vary
with environment even as the FP remains relatively constant; such a
detection would be an important constraint on formation mechanisms.
In this section (as in this review as a whole) we have focused mainly on the properties of the luminous galaxies. Just as dwarf disk galaxies deviate from the Tully-Fisher relation, the dE galaxies deviate from extrapolations of the FP (Geha, Guhathakurta & van der Marel 2003, van Zee, Skillman & Haynes 2004), while cE galaxies do not (Kormendy et al. 2009). However, low luminosity ellipticals do follow a more general, but still regular, relationship described by Zaritsky, Gonzalez & Zabludoff (2006), a "fundamental manifold" for spheroids.
5.5. Brightest cluster galaxies and cD galaxies
Among ellipticals, brightest cluster galaxies (BCGs) and cD galaxies
form a special class
(Morgan
& Lesh 1965,
Sandage 1972).
BCGs are usually defined as the highest optical luminosity galaxy in any
reasonably massive cluster (> 1014
M ). A large
fraction of BCGs have a larger associated distribution of stars that
extends out into the host cluster, called the "cD" envelope for
historical reasons, but sometimes referred to as the "intracluster
light" (ICL).
). A large
fraction of BCGs have a larger associated distribution of stars that
extends out into the host cluster, called the "cD" envelope for
historical reasons, but sometimes referred to as the "intracluster
light" (ICL).
In Figure 12, BCGs and galaxies with cD envelopes
are shown as the magenta dots. BCGs are luminous and massive, with a
log-normal distribution of stellar mass with a mean of
M∗
~ 2 × 1011 h-2
M and dispersion
and dispersion
 lnM ~ 0.4
(Lin & Mohr 2004,
Hansen et
al. 2009,
Yang, Mo & van
den Bosch 2008).
These luminosities are a function of
the host cluster mass, with LK
lnM ~ 0.4
(Lin & Mohr 2004,
Hansen et
al. 2009,
Yang, Mo & van
den Bosch 2008).
These luminosities are a function of
the host cluster mass, with LK
 Mh0.2-0.3
for massive clusters
(Lin et al. 2004,
Hansen et
al. 2009)
and a steeper relationship at lower masses
(Yang et al. 2007,
Brough et
al. 2008).
Thus, as the total halo mass and luminosity rises, the
fractional contribution of the BCG decreases.
Mh0.2-0.3
for massive clusters
(Lin et al. 2004,
Hansen et
al. 2009)
and a steeper relationship at lower masses
(Yang et al. 2007,
Brough et
al. 2008).
Thus, as the total halo mass and luminosity rises, the
fractional contribution of the BCG decreases.
Tremaine &
Richstone (1977)
found hints that BCGs were not merely the
brightest members of a randomly sampled luminosity function for each
cluster. In particular, the second brightest galaxy is normally at
least 0.8 mag fainter than the first. In contrast, if the luminosities
randomly sampled almost any conceivable distribution, then the
expected magnitude "gap" between the first and second ranked cluster
galaxies would be about the same or less than
 ln
M, or about 0.4 mag
(Vale & Ostriker
2008,
Loh & Strauss
2006).
This "gap" in magnitude suggests an anti-correlation among galaxy
luminosities within the same cluster.
ln
M, or about 0.4 mag
(Vale & Ostriker
2008,
Loh & Strauss
2006).
This "gap" in magnitude suggests an anti-correlation among galaxy
luminosities within the same cluster.
The dry merger, or cannibalism, scenario for the growth of BCGs is consistent with the last two results. First, the dynamical friction time scales for galaxies tends to increase as the host cluster mass increases, explaining why a smaller fraction of the cluster luminosity is accreted onto the central galaxy as mass increases (Cooray & Cen 2005). Second, if the second ranked galaxy is close in mass to the BCG, it is drawn preferentially to the BCG and will merge with it. This process will open a gap between the masses and luminosities of the first and second ranked galaxies (for recent analyses see Loh & Strauss 2006, Milosavljevic et al. 2006).
Other hints that BCGs are special come from comparing their
fundamental plane relation to that of other ellipticals. This
comparison is complicated by the fact that BCGs are much brighter
than the typical elliptical.
Oegerle &
Hoessel (1991)
reported that BCGs roughly followed the fundamental plane defined by
lower luminosity galaxies. However, above Mr -
5log10 h ~ -22.3 and
 ~ 280 km
s-1, the velocity dispersion of BCGs becomes
a weaker function of luminosity, causing a deviation from the
extrapolation of the fundamental plane. This weakening has been verified
in modern data sets
(Lauer et
al. 2007b,
von der
Linden et al. 2007,
Bernardi et
al. 2007,
Desroches et
al. 2007).
However, at luminosities where BCGs and elliptical
populations overlap, the differences in their velocity dispersions are
< 5%
(von der
Linden et al. 2007,
Desroches et
al. 2007).
~ 280 km
s-1, the velocity dispersion of BCGs becomes
a weaker function of luminosity, causing a deviation from the
extrapolation of the fundamental plane. This weakening has been verified
in modern data sets
(Lauer et
al. 2007b,
von der
Linden et al. 2007,
Bernardi et
al. 2007,
Desroches et
al. 2007).
However, at luminosities where BCGs and elliptical
populations overlap, the differences in their velocity dispersions are
< 5%
(von der
Linden et al. 2007,
Desroches et
al. 2007).
Several large studies based on SDSS also indicate that the most
luminous BCGs typically are larger than the radius-luminosity relation
for typical ellipticals would predict (r50
 L
L , with
, with
 ~ 0.6).
Either BCGs and other ellipticals lie on different loci in
r50 - L space, or the locus they both live on
is curved such that r50 is a
stronger function of L at high luminosity. In fact, there is
evidence that both effects exist. At higher luminosities, the non-BCG
ellipticals appear to deviate from a power-law relation
(Desroches et
al. 2007,
von der
Linden et al. 2007),
with a local power law
~ 0.6).
Either BCGs and other ellipticals lie on different loci in
r50 - L space, or the locus they both live on
is curved such that r50 is a
stronger function of L at high luminosity. In fact, there is
evidence that both effects exist. At higher luminosities, the non-BCG
ellipticals appear to deviate from a power-law relation
(Desroches et
al. 2007,
von der
Linden et al. 2007),
with a local power law
 varying from 0.5 at Mr - 5log10
h ~ -20 to 0.7 at
Mr - 5log10 h ~ -24. Simultaneously,
BCGs appear to be larger than non-BCGs at a given magnitude, but the
literature has not converged on the details.
von der
Linden et al. (2007)
find that the BCGs are all 10% larger on average than non-BCG
ellipticals, constant with luminosity, defining a slightly different
fundamental plane.
Desroches et
al. (2007),
meanwhile, find that the BCGs define a
steeper relationship than the ellipticals, and that at
Mr - 5 log10 h ~ -22 the typical BCG
is smaller than the typical elliptical.
Bernardi et
al. (2007)
also find a steeper slope for BCGs,
but that the relationships converge near Mr -
5log10 h ~ -22.
varying from 0.5 at Mr - 5log10
h ~ -20 to 0.7 at
Mr - 5log10 h ~ -24. Simultaneously,
BCGs appear to be larger than non-BCGs at a given magnitude, but the
literature has not converged on the details.
von der
Linden et al. (2007)
find that the BCGs are all 10% larger on average than non-BCG
ellipticals, constant with luminosity, defining a slightly different
fundamental plane.
Desroches et
al. (2007),
meanwhile, find that the BCGs define a
steeper relationship than the ellipticals, and that at
Mr - 5 log10 h ~ -22 the typical BCG
is smaller than the typical elliptical.
Bernardi et
al. (2007)
also find a steeper slope for BCGs,
but that the relationships converge near Mr -
5log10 h ~ -22.
These results suffer from two major systematic effects First, there are some significant ambiguities in defining a "BCG", particularly for cluster catalogs (e.g., Miller et al. 2005) based on an incomplete redshift survey like the SDSS (even 5%-10% incompleteness matters; see von der Linden et al. 2007). Second, BCGs are large objects on the sky, and their photometry is not handled correctly by the SDSS (Section 3; Lauer et al. 2007b). All of the work cited here either reanalyzes the images (Bernardi et al. 2007, Desroches et al. 2007) or corrects the catalog parameters in an ad hoc way (von der Linden et al. 2007). No cross-comparison of their analyses has been published.
Many BCGs have an extended distribution of stars that is inconsistent with a single de Vaucouleurs profile extrapolated from small radii, or even with a more general Sérsic profile, known as a cD envelope or the ICL. Mihos et al. (2005) found that the Virgo Cluster has a particularly dramatic ICL component, with visible streams and other features that might suggest a tidal stripping or merging scenario for its formation. For a large sample of clusters, Gonzalez, Zabludoff & Zaritsky (2005) recently showed that detected ICL components are often discernably separate entities from the host BCGs, with well defined transitions in the surface brightness profile, axis ratio, and position angle. Zibetti et al. (2005) stacked images of many different SDSS clusters and statistically detected the ICL component. Zibetti et al. (2005) and a study of individual detections by Krick & Bernstein (2007) both conclude that of order 5%-20% of the total cluster optical light within 500 kpc or so comes from the ICL; the results of Gonzalez, Zabludoff & Zaritsky (2005) imply even more. If so, the stellar mass in the ICL is comparable to that in the BCG itself (or possibly 4-5 times the BCG mass if the analysis of Gonzalez, Zabludoff & Zaritsky (2005) is correct). Its existence appears consistent with the merger hypothesis for BCGs themselves.
The dynamics of the ICL component is poorly known in most cases, and
it is unclear to what degree is represents the dynamics of the cluster
as a whole. Some BCGs show the rising velocity dispersion profile at
large radius expected from the cluster dark matter distribution (most
notably those found in
Dressler 1979,
Kelson et
al. 2002).
However, the large studies of
Fisher,
Illingworth & Franx (1995)
and
Loubser et
al. (2008)
find that only a minority of cD envelopes have such a profile.
Interestingly, detectable rotation is seen in a number of cD
envelopes, with V /
 ~ 0.3.
~ 0.3.
5.6. Deviations from smooth profiles
In addition to boxiness and diskiness, elliptical galaxies often show other deviations from smooth elliptical isophotes, at least at very faint levels (Kormendy & Djorgovski 1989). The most common deviation from smoothness is due to dust features; as we outline in Section 5.8, many elliptical galaxies have a small but detectable amount of cold gas and associated dust. For example, Colbert, Mulchaey & Zabludoff (2001) find that about 75% of ellipticals have detectable dust extinction in the optical, irrespective of environment.
Elliptical galaxy profiles also often reveal shells or ripples, and other signs of recent interaction (Athanassoula & Bosma 1985). While Malin & Carter (1983) found that about 10% of all ellipticals had detectable features, perhaps unsurprisingly it appears that deeper observations reveal structure in a larger fraction. van Dokkum (2005) find that 70% of ellipticals have detectable tidal features down to 27-28 mag arcsec-2. For about 20% of those detections, a secondary object that appears responsible for the features is observed. These observations suggest that some growth of elliptical galaxies occurs through merging; however, precisely how much is difficult to infer from such observations. Colbert, Mulchaey & Zabludoff (2001) also searched their sample for tidal features, finding that the fraction of disturbed ellipticals is a strong function of environment, more common in isolated regions than in groups and clusters. Finally, ellipticals with more fine structure tend to be slightly bluer than those with less (Schweizer & Seitzer 1992) and perhaps lie on the bright side of the fundamental plane (Michard & Prugniel 2004).
A final deviation from a purely elliptical profile is that of isophotal twists. These features, which can be caused by triaxiality or by tidal effects, appear to be rare: a survey of Virgo ellipticals using HST / ACS reported only seven cases of isophotal twisting (some of these very marginal or related to central disks) out of 100 observed early-type galaxies (Ferrarese et al. 2006).
The spectra of elliptical galaxies are dominated by emission from the
surfaces of stars, typically K giants but comprising some mixture of
stellar types depending on the age, metallicity, and metal abundances of
the stellar population. For this reason ellipticals all have nearly
the same optical broad-band color, with a weak dependence of color on
galaxy luminosity (and equivalently, stellar mass or velocity
dispersion). This dependence is due to both age and metallicity trends
as a function of mass, as detailed spectroscopic analyses reveal.
Renzini (2006)
review the subject in detail. However, in brief,
Balmer absorption lines such as
H ,
H
,
H and
H
and
H tend
to trace age in old stellar populations, while metal-line indices such
as <Fe>; and Mg b yield information about the
metallicity and
tend
to trace age in old stellar populations, while metal-line indices such
as <Fe>; and Mg b yield information about the
metallicity and  abundances
in the stellar atmospheres.
abundances
in the stellar atmospheres.
Based on high signal-to-noise optical spectroscopy of morphologically
selected E and S0 galaxies,
Thomas et
al. (2005)
show that the
metallicity (or iron abundance) and
[ / Fe] ratio are both
correlated with velocity dispersion (or mass). As found previously,
the Mg b indicator is much more tightly correlated to mass than
<Fe> (e.g.
Worthey 1998
and references therein). Similar
results have also been found with large samples of (lower
signal-to-noise) SDSS galaxies (e.g.,
Eisenstein et
al. 2003,
Bernardi et
al. 2006,
Gallazzi et
al. 2006,
Jimenez et
al. 2007).
/ Fe] ratio are both
correlated with velocity dispersion (or mass). As found previously,
the Mg b indicator is much more tightly correlated to mass than
<Fe> (e.g.
Worthey 1998
and references therein). Similar
results have also been found with large samples of (lower
signal-to-noise) SDSS galaxies (e.g.,
Eisenstein et
al. 2003,
Bernardi et
al. 2006,
Gallazzi et
al. 2006,
Jimenez et
al. 2007).
Many ellipticals show evidence for recent star formation in their
optical spectra, and the incidence is higher in lower-mass galaxies
(Trager et
al. 2000,
Thomas et
al. 2005).
These conclusions have been strengthened by recent observations with
GALEX.
Yi et al. (2005),
Kaviraj et
al. (2007),
and
Schawinski et
al. (2007)
have all found evidence for recent
(  1 Gyr) star
formation in 15%-30% of morphologically selected elliptical galaxies, which
accounts for 1%-3% of the stellar mass of the galaxy.
1 Gyr) star
formation in 15%-30% of morphologically selected elliptical galaxies, which
accounts for 1%-3% of the stellar mass of the galaxy.
There appears to be some variation of these star-formation histories
with environment. Figure 15 shows
H ,
<Fe> and Mg b as a function of velocity
dispersion
,
<Fe> and Mg b as a function of velocity
dispersion  for E/S0
galaxies from
Thomas et
al. (2005).
Filled symbols correspond to galaxies in dense
regions, while unfilled symbols are for galaxies in underdense
regions. They appear to lie on somewhat different loci. According to
Thomas et
al. (2005),
based on these results the field early-type
galaxies are on average ~ 2 Gyr younger and slightly more
metal-rich, while both populations show comparable
[
for E/S0
galaxies from
Thomas et
al. (2005).
Filled symbols correspond to galaxies in dense
regions, while unfilled symbols are for galaxies in underdense
regions. They appear to lie on somewhat different loci. According to
Thomas et
al. (2005),
based on these results the field early-type
galaxies are on average ~ 2 Gyr younger and slightly more
metal-rich, while both populations show comparable
[ / Fe]
ratios.
Bernardi et
al. (2006)
found qualitatively similar results,
though with a rather different analysis technique.
Schawinski et
al. (2007)
further found that early-types with recent star
formation were more prevalent in low density environments, even after
controlling for the fact that lower-mass (massive) galaxies are found
preferentially in underdense (dense) regions.
/ Fe]
ratios.
Bernardi et
al. (2006)
found qualitatively similar results,
though with a rather different analysis technique.
Schawinski et
al. (2007)
further found that early-types with recent star
formation were more prevalent in low density environments, even after
controlling for the fact that lower-mass (massive) galaxies are found
preferentially in underdense (dense) regions.
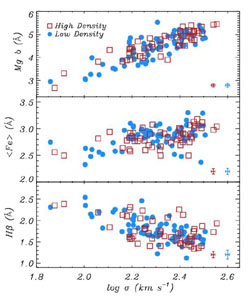 |
Figure 15. Dependence of E/S0 spectral
indices on |
The nature of elliptical galaxy stellar populations is an old, storied, and quite controversial one, and the limited space here cannot do it justice. However, we do note several investigations that have reached conclusions in conflict with those described above. First, recent Spitzer observations of the mid-IR (9-12 µ) spectra of ellipticals in nearby clusters have found that the vast majority are consistent with being purely passively evolving systems (Bressan et al. 2006, Bregman, Temi & Bregman 2006). Second, Trager, Faber & Dressler (2008) find that early-type galaxies in the Coma cluster show the same mean age as field ellipticals (though less scatter). The exact nature of the recent star formation in ellipticals, and its variation with environment, therefore appears to be in some doubt.
Elliptical galaxies contain a small amount of cold atomic and
molecular interstellar gas
(Faber &
Gallagher 1976).
When detected, the gas comprises
 1% of the total
mass of the system
(Knapp, Turner
& Cunniffe 1985),
so it is not a dominant baryonic component.
1% of the total
mass of the system
(Knapp, Turner
& Cunniffe 1985),
so it is not a dominant baryonic component.
Early observations showed that the H i detection rates in ellipticals are several times higher in objects with morphological fine structure such as visible dust lanes, shells, and ripples (Bregman, Hogg & Roberts 1992, van Gorkom & Schiminovich 1997), which themselves occur more frequently in field ellipticals (Malin & Carter 1983, Schweizer et al. 1990). This result indicates a close connection between the gas properties of a galaxy and visible signs of interaction.
The morphology of the
H i gas in early-type
galaxies generally
falls into two categories: most have disk- or ring-like structures
with regular kinematics, extending up to ~ 200 kpc in diameter,
while in others the H i
appears in an irregular, tail-like structure or in individual clouds
that are offset from the center of the galaxy
(Morganti et
al. 2006,
Oosterloo et
al. 2007).
Morganti et
al. (2006)
surveyed a representative subset of the SAURON galaxies and detected
H i emission in 70% of
the sample, with gas masses ranging from 106 to 109
M . They
found that
galaxies with H i
disks had the most ionized gas emission (see also
Serra et al. 2008),
but that the H i
properties were uncorrelated with either the age of the stellar
population or the stellar kinematics (fast vs. slow rotators).
Thus, most early-types seem to accumulate at least some gas,
irrespective of their evolutionary past.
. They
found that
galaxies with H i
disks had the most ionized gas emission (see also
Serra et al. 2008),
but that the H i
properties were uncorrelated with either the age of the stellar
population or the stellar kinematics (fast vs. slow rotators).
Thus, most early-types seem to accumulate at least some gas,
irrespective of their evolutionary past.
Surveys of molecular gas in elliptical galaxies have also rapidly advanced, although the samples remain relatively sparse. Combes, Young & Bureau (2007) reported that 28% of the SAURON sample has detectable CO. Similarly, Sage, Welch & Young (2007) detected CO emission in 33% of a volume-limited sample of field ellipticals; their survey was designed to detect at least 1% of the gas expected to have been returned to the interstellar medium by evolved stars in a Hubble time. From interferometric mapping, the molecular gas is typically in a rotationally supported disk 2-12 kpc in diameter (Young 2002, Young 2005). In many cases these gas disks contain higher specific angular momentum than the stars, or are counter-rotating with respect to the stars, suggesting an external origin (Young, Bureau & Cappellari 2008).
The analysis by Combes, Young & Bureau (2007) of CO-rich early-type galaxies also found that their sample obeyed the Kennicutt-Schmidt relation (Section 3.5; Kennicutt (1998b)) for disk and starburst galaxies, but at gas and star formation rate surface densities two orders of magnitudes lower. Further evidence for ongoing star formation in early-type galaxies was presented by Young, Bendo & Lucero (2008), who studied a sample of CO-rich E/S0 galaxies and found good spatial correspondence between the CO, 24 µm, and radio continuum emission, from which they concluded that the 24µm emission is predominantly due to star formation (rather than AGN or circumstellar in origin).
The nature of the gas in ellipticals is mysterious. Stellar recycling arguments suggest that they should contain about ten times the atomic hydrogen mass that they actually do. Additionally, the gas mass is not correlated with the stellar mass, which it would be if recycling were an important source (Ciotti et al. 1991, Sage, Welch & Young 2007). Where the recycled gas goes is an unsolved problem.