3. ESTIMATES OF COSMIC-RAY ENERGY DENSITY

Active star formation in galaxies leads to acceleration of protons and electrons via the Fermi-I diffusive shock acceleration mechanism in SN remnants. Under equilibrium conditions in a galaxy, a minimum-energy configuration of the magnetic field and the energetic particles may be attained. Energy densities of particles and magnetic fields may then be in approximate equipartition, implying that the energetic proton energy density, U_p, can be deduced from the detected level of synchrotron radio emission. In this radio-based approach U_p can be estimated if the source size, distance, radio flux, and radio spectral index are known.

In a -based approach, U_p can be obtained from the measured GeV-TeV spectral flux, which is mostly due to p-p interactions, as described the previous section. Only recently have such measurements become possible, at present only for 10 sources.

In the SN method, with an assumed fraction of SN kinetic energy that is channeled into particle acceleration, U_p can be estimated if the size of the star-forming region and SN rate are known, as well as an estimate for the proton residence timescale from the presence (or absence) of a galactic wind emanating from the star-forming region. This timescale is largely determined by the advection timescale (~ 10⁵yr) in SBGs, and by the ⁰-decay timescale (~ 10⁷yr) in low-SFR (quiescent) galaxies.

Expanding on our previous work (Persic & Rephaeli 2010), we show that the three methods give consistent results for U_p for a sample of 10 galaxies with widely varying levels of star formation activity, from very quiescent to extreme SBs. These are the only galaxies of their kind for which -ray data, in addition to radio data and SN rates, are available (see Table 1).

Table 1. Star-forming galaxies: the data.

Object	DL[1]	rs[2]	f1 GHz[3]	NT[4]	ne, th[5]	LTIR[6]	SFR[7]	SN[8]	Mgas[9]	L[10]	Notes
	(Mpc)	(kpc)	(Jy)		(cm-3)	(erg/s)	(M/yr)	(yr-1)	(M)	(erg/s)
Arp 220	74.7	0.25	0.3	0.65	300	45.75	253	3.5	9.24-0.11+0.10	< 42.25	SB
M 82	3.4	0.23	10.0	0.71	200	44.26	8.2	0.25	9.37-0.14+0.09	40.21-0.13+0.10	SB
NGC 253	2.5	0.20	5.6	0.75	400	44.23	7.7	0.12	9.20-0.11+0.10	39.76-0.19+0.14	SB
Milky Way	–	4.4	–	–	0.01	43.75	2.5	0.02	9.81-0.16+0.12	38.91-0.15+0.12	quiescent
M 31	0.78	4.5	4.0	0.88	0.01	42.98	0.43	0.01	9.88-0.15+0.11	38.66-0.10+0.09	quiescent
M 33	0.85	2.79	3.30	0.95	0.03	42.68	0.22	0.003	9.35-0.19+0.13	< 38.54	quiescent
LMC	0.049	2.4	285.0	0.84	0.01	42.45	0.13	0.002	8.86-0.18+0.12	37.67-0.05+0.05	quiescent
SMC	0.061	1.53	45.3	0.85	0.01	41.45	0.01	0.001	8.66-0.06+0.03	37.04-0.14+0.11	quiescent
NGC 4945	3.7	0.22	5.5	0.57	300	44.02	4.7	0.1-0.5	9.64-0.40+0.10	40.30-0.16+0.12	SB+Sy2
NGC 1068	16.7	1.18	6.6	0.75	300	45.05	50	0.2-0.4	9.71-0.19+0.11	41.32-0.23+0.15	SB+Sy2
[1]Distance (from Ackermann et al. 2012). [2]Effective radius of star-forming region. See text. Data are from Persic & Rephaeli 2010 and refs. therein (Arp 220, M 82, NGC 253), Beck & Gräve 1982 (M 31), Tabatabaei et al. 2007 (M 33), Weinberg & Nikolaev 2001 (LMC), Wilke et al. 2003 (SMC), Moorwood & Oliva 1994 ( NGC 4945), Spinoglio et al. 2005 (NGC 1068). [3]1 GHz flux density. Data are from Persic & Rephaeli 2010 and refs. therein (Arp 220, M 82, NGC 253)), Beck & Gräve 1982 (M 31), Tabatabaei et al. 2007 (M 33), Klein et al. 1989 (LMC), Haynes et al. 1991 (SMC), Elmouttie et al. 1997 ( NGC 4945), Kühr et al. 1981 (NGC 1068). [4]Non-thermal spectral radio index. Data are from Persic & Rephaeli 2010 and refs. therein (Arp 220, M 82, NGC 253), Beck & Gräve 1982 (M 31), Tabatabaei et al. 2007 (M 33), Klein et al. 1989 (LMC), Haynes et al. 1991 (SMC), Elmouttie et al. 1997 ( NGC 4945), Kühr et al. 1981 (NGC 1068). [5]Thermal electron density. Data are from Roy et al. 2010 (Arp 220), Petuchowski et al. 1994 (M 82), Kewley et al. 2000 and Corral et al. 1994 (NGC 253), Cox 2005 (Milky Way), Beck 2000 (M 31), Tabatabaei et al. 2008 (M 33), Points et al. 2001 (LMC), Sasaki et al. 2002 (SMC), Spoon et al. 2000 (NGC 4945), Kewley et al. 2000 (NGC 1068). [6]Total IR [i.e., (8-1000)µm] luminosity, in log (from Ackermann et al. 2012). [7]Star formation rate, from SFR = LIR / (2.2 × 1043 erg/s ) (Kennicutt 1998). [8]Core-collapse SN rate. Data are from Persic & Rephaeli 2010 and references therein (Arp 220, M 82, NGC 253), Diehl et al. 2006 (Milky Way), van den Bergh & Tammann 1991 (M 31, M 33, SMC, LMC; see also Pavlidou & Fields 2001), Lenain et al. 2010 and references therein (NGC 4945, NGC 1068). For NGC 1068 we also computed an upper limit to the SN rate (SN 0.39) using Mannucci et al.'s (2003) formula SN = (2.4 ± 0.1) × 10-2 [LFIR / (1010 L)] yr-1, being fFIR = 1.26 × 10-11(2.58 f60 + f100) erg cm-2s-1 (see Helou et al. 1988) with f60 190 Jy and f100 277 Jy. [9]Gas mass (neutral plus molecular hydrogen: MHI + MH2), in log. Data are from: Torres 2004 for Arp 220; Abdo et al. 2010a for M 82, NGC 253, and the Milky Way; Abdo et al. 2010b for M 31 and M 33Abdo et al. 2010c for the LMC; Abdo et al. 2010d for the SMC; and Lenain et al. 2010 for NGC 4945 and NGC 1068. [10]High-energy (> 100 MeV) -ray luminosity, in log (from Ackermann et al. 2012).

3.1. Particles and magnetic field

The population of NT electrons consists of primary (directly accelerated) and secondary (produced via ^± decays) electrons. While the exact form of the steady-state electron energy spectrum is not a single power law, at high energies the flattening of the spectrum due to Coulomb losses can be ignored, justifying the use of the approximate single power-law form. The combined (primary plus secondary) electron spectral density distribution is then

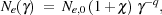(1)

where the electron Lorentz factor is in the range 1 2, Ne,0 is a normalization factor of the primary electrons, is the secondary-to-primary electron ratio, and q 2 is the spectral index. Ignoring the contribution of low-energy electrons with < 1, the electron energy density is Ue = Ne,0 (1 + ) me c2 ∫12 1-q d, where 2 is an upper cutoff whose exact value is irrelevant in the limit of interest, 2 >> 1. For q > 2 and 2 >> 1,

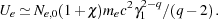(2)

For a population of electrons (specified by Eq. 1) traversing a homogeneous magnetic field of strength B in a region with (a spherically equivalent) radius r_s located at a distance d, standard synchrotron relations yield

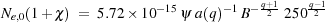(3)

where the scaled flux is f_{1 GHz} Jy, a(q) is defined and tabulated in, e.g., Tucker (1975), and (r_s / 0.1 kpc)^-3 (d / Mpc)² (f_{1 GHz} / Jy). Use of Eq.(2) then yields

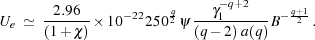(4)

In order to compute U_e from Eq.(4) we need to specify ₁ and B. To do so we make the following assumptions:

(i) The low-energy limit of the electron power-law spectrum, ₁, marks the transition (for decreasing energy) from Coulomb (Rephaeli 1979) to synchrotron losses. For an electron of energy , the synchrotron loss rate is

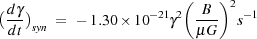(5)

whereas the Coulomb loss rate is

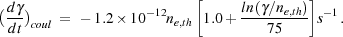(6)

(Rephaeli 1979). We then simply assume that electrons lose energy via Coulomb scattering for < ₁ and via synchrotron cooling for > ₁.

(ii) The particle energy density is in equipartition with that of the magnetic field, U_p + U_e = B² / 8 . In terms of the p/e energy density ratio, , the equipartition condition is U_p [1+ (1 + ) / ] = B² / 8, so that

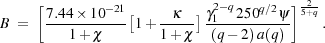(7)

Inserting Eq.(7) into Eq.(5) we get (d / dt)_{syn 1}^{2(9-q) / (5 + q)}. Once the value of n_e,th is specified (see Table 1), by equating Eqs.(5, 6) we deduce ₁.

The secondary-to-primary electron ratio , which appears in Eq.(7), depends on the injection p/e number ratio, r_p/e = (m_p / m_e)^(q_inj-1)/2, and on the gas optical thickness to p-p interactions. Given the branching ratios in p-p collisions, only a third of these collisions produce electrons. The mean free path of CR protons due to p-p interactions in a medium of density n_p is _pp = (_pp n_p)^-1; for protons with kinetic energy T ~ few TeV the cross section is _pp 50 mb = 5 × 10^-26 cm² (Baltrusaitis et al. 1984). For a typical SB ambient gas density n_p 150 cm^-3, _pp ~ 43 kpc. The probability for a single CR proton to undergo a pp interaction in its 3D random walk through a region of radius r_s ~ 0.25 kpc (also typical of SB nuclei) is then √3 r_s / _pp 0.01. Thus, in a typical SB environment, characterized by relatively strong non-relativistic shocks (q_inj = 2.2), the secondary to primary electron ratio is = ₀ √3 (r_s / _pp) 0.3. In a more quiescent environment, with typical values n_p 1 cm^-3 and r_s ~ 2.5 kpc, 0.03. The higher value found in SBs is in approximate agreement with results of detailed numerical starburst models for energies 10 MeV (plotted in, e.g., Paglione et al. 1996, Torres 2004, De Cea et al. 2009, Rephaeli et al. 2010).

To compute the p/e energy density, , we assume power-law spectra: (i) The electron spectral index q_e is deduced from the measured radio index , generally q_e = 2 + 1. (ii) The proton spectral index is assumed to be close to the injection value, q_p ~ q_inj 2.1-2.2, for the dense SB environments hosted in the central regions of some galaxies, and equal to the leaky-box value, q_p = q_inj + 2.7 (where 0.5 is the diffusion index) for more quietly star forming galaxies.

Finally, we obtain an explicit expression for U_p:

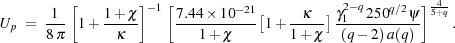(8)

Using Eq.(8), values of U_p can be obtained from the relevant observational quantities for our sample galaxies; these values are listed in Table 2. The quantities in Eq.(8) are usually well determined for our sample galaxies, except for the p/e energy density ratio , for which a spectral index, q_p, must be assumed. Given its possible values (i.e., q_p 2.1-2.2 in SB regions, and q_p 2.1-2.2 for quiescent galaxies), the uncertainty in the spectral index, q_p 0.1, translates to a factor of ~ 2 uncertainty on , i.e. typically an uncertainty of ~ 50% on U_p as deduced from Eq.(8).

3.2. Energetic particles and -ray emission

Based on the calculation of -ray emission from SFGs outlined in Section 1, U_p can be estimated directly from recent measurements of the nearby galaxies. In SBGs, such as M 82 and NGC 253, the central SB region (referred to also as the source region) with a radius of ~ 200-300 pc is identified as the main site of particle acceleration. The injected particle spectrum is assumed to have an index q = 2, the theoretically predicted N_p / N_e ratio is adopted, and equipartition is assumed. A measured radio index 0.7 in the source region implies q = 2 + 1 2.4 there, indicating a substantial steepening due to diffusion (D ^-), that cause the steady-state particle spectral index to be q₀+ above some break energy. The procedure is similar when star formation does not (largely) occur in a burst in the nuclear region, but proceeds more more uniformly across the disk.

For a source with ambient gas number density n_gas, proton energy density U_p, and volume V, the integrated hadronic emission from pp-induced ⁰ decay is

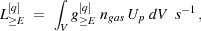(9)

with the integral emissivity g ^[] in units of photon s^-1(H-atom)^-1(eV/cm³)^-1 (Drury et al. 1994). Thus, U_p can be determined from measurements of L and n_gas(r), and the particles steady-state energy distributions can be numerically calculated in the context of the convection-diffusion model.

In addition to the high-energy detections of the two local SBGs M 82 and NGC 253 (Abdo et al. 2010a, Acciari et al. 2009; Acero et al. 2009), several galaxies with low SFR were also detected by the Fermi telescope. (i) the Andromeda galaxy M 31 (Abdo et al. 2010b), with U_p 0.35 eV cm^-3; (ii) the Large Magellanic Cloud (LMC) whose average spectrum, either including or excluding the bright star-forming region of 30 Doradus, suggests U_p 0.2-0.3 eV cm^-3 (Abdo et al. 2010c); (iii) SMC for which U_p 0.15 eV cm^-3 was deduced (Abdo et al. 2010d). For the Milky Way, the modeling of the Galactic diffuse HE emission along the lines outlined above requires an average U_p 1 eV cm^-3 (Strong et al. 2010; Ackermann et al. 2011). Our values for U_p determined from the measured GeV-TeV fluxes are listed in Table 2.

3.3. Energetic particles and Supernovae

The SN origin of energetic particles suggested early on; as a test of this hypothesis, we estimate of U_p by combining the SN rate with the proton residence time, _res, assuming a fiducial value for the fraction of SN kinetic energy that is channeled to particle acceleration. The residence time is determined from the p-p interaction time, and the two propagation timescales of advection and diffusion:

(i) The energy-loss timescale for pp interactions, _pp = (_pp c n_p)^-1; for protons with kinetic energy E 10 TeV for which _pp 50 mb, this timescale is

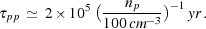(10)

(ii) Particle advection out of the disk mid-plane region in a fast SB-driven wind occurs on a timescale _adv determined from the advection velocity for which we adopt (except where noted otherwise) the nominal value v_adv ~ 1000 km s^-1, deduced from measurements of the terminal outflow velocity of ~ 1600-2200 km s^-1 in M 82 (Strickland & Heckman 2009; see also Chevalier & Clegg 1985 and Seaquist & Odegard 1991). For a homogeneous distribution of SNe within the SB nucleus of radius r_s, the advection timescale is

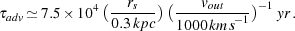(11)

(iii) As noted in the previous section, diffusion is likely to be random walk against magnetic field inhomogeneities, with an estimated central diffusion coefficient, D ~ 3 × 10²⁸ cm²/s, assuming a magnetic coherence scale of ~ 1 pc. Thus, diffusion out of the central 0.5 kpc is estimated to occur on a timescale

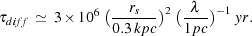(12)

Now, since the weighted residence time is

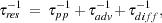(13)

it is expected that - under typical conditions in central SB regions - p-p collisions and advection, more so than diffusion, effectively determine the survival there of energetic protons.

During _res, the number of SN is _{SN res}; the kinetic energy deposited by each of these into the ISM is E_ej = 10⁵¹ erg (Woosley & Weaver 1995). Arguments based on the energetic particle energy budget in the Galaxy and SN statistics suggest that a fraction ~ 0.05-0.1 of this energy is available for accelerating particles (e.g., Higdon et al. 1998). Thus, the proton energy density can be expressed as

(14)

The resulting values of U_p in the sample galaxies are listed in Table 2.

Table 2. Star-forming galaxies: Proton energy densities⁺.

Object	-ray	radio	SN	other	rs	res
	meth.	meth.	meth.	meth.	(kpc)	(yr)
Arp 220	–	1027	1142	–	0.25	2.0E+4
M 82	250a,c	250	234	–	0.23	4.5E+4
NGC 253	220b,c	230	213	–	0.20	6.7E+4
Milky Way	1d	–	1.2	1j	4.4	2.0E+7
	6e	–	5	–	0.2	2.5E+6
M 31	0.36f	0.22	0.7	–	4.5	2.5E+7
M 33	<0.43f	0.38	0.7	–	2.8	2.0E+7
LMC	0.21-0.31g	0.22	0.4	–	2.5	4.4E+7
SMC	0.15h	0.39	1.1	–	1.5	1.4E+7
NGC 4945	200i	201	215	–	0.22	4.5E+4
NGC 1068	–	65	61	–	1.2	1.0E+6
+ Values are in eV cm-3. (a) Acciari et al. (2009; see also Persic et al. 2008, De Cea et al. 2009). (b) Acero et al. (2009). (c) Abdo et al. (2010a). (d) Strong et al. (2010). (e) Aharonian et al. (2006). (f) Abdo et al. (2010b), and Drury et al. (1994) for M 33. (g) Abdo et al. (2010c). (h) Abdo et al. (2010d). (i) Lenain et al. (2010). (j) Webber (1987).