


The RHS and VRHS classifications have always had a problem with early-type galaxies:
the En classification has no physical significance, unlike the stage classification for spirals;
the properties of S0s do not support the idea of them being a transition class between ellipticals and Sa, SBa galaxies (van den Bergh 1976, 1998).
Van den Bergh (1976) challenged the tuning fork by following the suggestion of Spitzer & Baade (1951; also Baade 1963) that S0s probably form a sequence parallel to spirals, rather than being in the juncture of the tuning fork between ellipticals and spirals. In a revised classification, van den Bergh proposed that S0s be classified as a sequence S0a - S0b - S0c parallel to the regular Hubble spiral sequence classification Sa - Sb - Sc (Fig. 19, lower left). In between these two sequences is a sequence of `anemic spirals': Aa - Ab - Ac, meaning spirals whose lower than average star formation rate and dust content implied a deficiency of Hi gas (discussed further in Lecture 4, Section 7). This view of the S0s is called `parallel sequence classification'. Although a reasonable point of view, the van den Bergh sequence did not gain much traction at least in part because of the absence, until recently, of any S0s than might be identified as type S0c.
Several recent studies have provided strong support for the parallel sequence idea:
Kormendy & Bender (2012): Sph galaxies & E galaxy dichotomies; edge-on disks embedded in environmentally modified Sph galaxies; S0c galaxy identified;
Cappellari et al. (2011): ATLAS3D kinematic classifications;
Laurikainen et al. (2011): Near-IR S0 Survey (revised view of S0 bulges and identification of some of the first van den Bergh S0c galaxies).
The problem with the En classification was at least partly solved by Kormendy & Bender (1996) who modified the Hubble E galaxy sequence to distinguish boxy versus disky Es (Fig. 19, upper right). Boxy Es show isophotes that have a negative value of the relative Fourier radius parameter a4 / a (Jedrezjewski 1987), are more luminous, have less rotation, and more velocity dispersion anisotropy than disky Es, which have a positive value of a4 / a. Figure 19 (upper left) shows two extreme examples of boxy and disky Es where the character is evident by eye. The E(b)5 is NGC 7029 while the E(d)5 is NGC 4697.
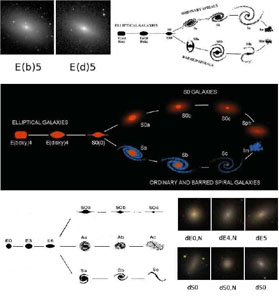 |
Figure 19. Two revisions of the Hubble tuning fork by Kormendy & Bender (1996, 2012). The van den Bergh (1976) parallel sequence classification schematic is shown at lower left, and several Sph galaxies are shown at lower right. All three modified tuning forks are reproduced with permission of the authors |
Further studies of E galaxies revealed that galaxies classified as dwarf ellipticals in the Virgo cluster are NOT the low-luminosity versions of regular ellipticals (Kormendy 1985; Kormendy et al. 2009). Instead, as we noted in the previous section, dE and dS0 galaxies are the progeny of late-type galaxies. Kormendy & Bender's (2012) reclassification of these objects as Sph galaxies, and their suggested location in parallel sequence classification is shown in Fig. 19, middle. Several examples are shown in Fig. 19, lower right.
Kormendy et al. (2009) carried out a very detailed study of high- and low-luminosity E galaxies and Sph galaxies. An E galaxy dichotomy exists in the sense that luminous Es have a `core' (an inner radial zone of what seems like `missing light', like a cone cut off at the top), while lower-luminosity Es appear to lack this missing light core, instead showing `extra light' in the manner of a power-law excess. B13 shows a comparison between three nucleated Sph galaxies and three genuine E galaxies (one of the core type, and two of the power-law type). Although the subtle differences are evident directly, the distinctions are best seen in the profiles and parameter correlations described by Kormendy et al. (2009).
ATLAS3D was a massive study of the detailed kinematics of 260 early-type galaxies (Emsellem et al. 2007, 2011; Cappellari et al. 2011). Based on a kinematic parameter, λR, Cappellari et al. (2011) independently came to the same conclusion as Kormendy & Bender (2012): the correct placement of S0s is parallel to spirals. Cappellari et al. (2011) showed that the best way to order early-type galaxies is kinematically, not morphologically. Their proposed revision to the Hubble tuning fork is shown in Fig. 20.
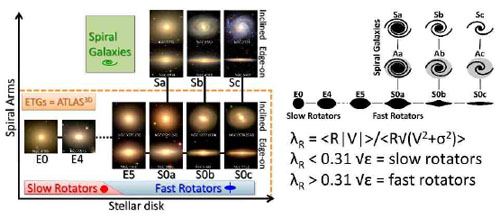 |
Figure 20. Atlas3D kinematic basis for parallel sequence classification, from Cappellari et al. (2011, reproduced with permission). |
The contribution of Laurikainen et al. (2011) to the parallel sequence classification idea involves the use of sophisticated two-dimensional photometric decomposition that led to both a revised view of the significance of S0 bulges (bulge-to-total luminosity ratio) and the discovery of a few genuine S0c galaxies. This is discussed further in Lecture 3 (Section 6).
Note that none of this necessarily completely negates the value of tuning fork classifications, because types such as En, S01, S02, S03, or E+n, S0-, S0°, and S0+ are still morphologically valid visual categories. A galaxy may be classified as type SA(rl)0+ and S0b, and the two classifications are more complimentary than contradictory. The same is true for the dE and dS0 categories. The revised tuning fork clarifies relationships between types and, most importantly, finds a proper `home' for the enigmatic Sph/dE/dS0 galaxies in the Hubble sequence.
The revisions to the tuning fork represent the coming to fruition of quantitative and interpretive galaxy classification. Quantitative morphology relies on derived photometric or kinematic parameters to determine relations between galaxy types such as, for example, the relation between spheroidal galaxies and Magellanic irregular galaxies, normal ellipticals and compact ellipticals, disky ellipticals and disk galaxies, and between spirals and S0s. Interpretive galaxy classification means `with a particular idea in mind', such as the nature versus nurture origin of S0 galaxies, or, for example, different subtypes of outer pseudorings (see Lecture 2, Section 5).
4.1. Does the continuity of galaxy morphology imply that secular evolution must be occurring?
To some extent it probably does, but apparent continuity can be misleading. For example, the VRHS classification of S0s from featureless systems with only a trace of a lens to systems with obvious rings or traces of spiral structure is clear continuity in galaxy morphology, but it does not necessarily mean that the placement of S0s between ellipticals and spirals is correct. The type `S0/a' automatically suggests a correct placement. Even so, some aspects of the VRHS could imply secular evolution, such as:
The smooth variation in bar strength (with numerous examples filling the continuum of forms from SA to SB). Does this imply evolution from SB to SA or vice-versa, or both? The simulations of Bournaud & Combes (2002) suggest that bar destruction by increasing central mass concentration followed by bar rejuvenation by external gas accretion could keep `apparent bar strength' as a continuum of forms just as recognised in the VRHS.
The seemingly smooth connection between rings and lenses. These features are found in the same general locations relative to bars, and in particular the radial profile of a lens can be very much like a ring of lower contrast on a steeply declining background [e.g., the lens of NGC 1553 (Kormendy 1984); as compared to the bright stellar inner ring of NGC 7702 (Buta 1991; see Fig. 20 of Buta & Combes 1996)]. Do lenses simply represent the dissolution of bars or bar-like features, or could many lenses be diffused (highly evolved) former rings? The latter could follow from the mere existence of inner, outer, and nuclear lenses in the same manner as inner, outer, and nuclear rings. Nevertheless, the virtually one-to-one connection between the sizes of bars and the diameters of inner lenses still suggests, as noted by Kormendy (1979), that such lenses formed by bar dissolution. A study of lens colours would aid greatly in further establishing these connections.
The smooth variations in ring morphologies, ranging from completely closed features to no ring at all, with a continuum of `pseudorings' in between. Does this mean that pseudorings evolve secularly into closed rings? Does it also mean that a galaxy with no ring could eventually become ringed? Even the simplest numerical simulations, such as those of Schwarz (1981, 1984a), Simkin et al. (1980), and Byrd et al. (1994), suggest that it might be possible for gravity torques acting on spiral segments to evolve a pseudoring pattern and eventually close it. It is not clear from such simulations, however, that pure (s)-variety spirals could evolve into pure (r)-variety spirals. Such evolution could depend on the evolution of the bar pattern speed as well.
The smooth variations in morphology along the spiral type sequence. Could a spiral evolve along this sequence? Could it do this without also evolving along the family and variety dimensions of the VRHS? Stage evolution is perhaps the most important question we could ask about secular galaxy evolution, because it brings us into the realm of bulge formation and evolution. If many bulges are built up by secular movement of disk material (as opposed to multiple mergers), then secular evolution from late-to-early would indeed be possible (KK04). A big question is, how many `steps' in stage could a galaxy evolve in this way during a Hubble time? I did not discuss `pseudobulges' during my actual lectures since these were covered in some detail by Kormendy (this volume), but in the next set of notes I will describe the morphologies of such bulges.