5. Lecture 2: BARRED AND SPIRAL GALAXIES

In my second lecture I would like to introduce the important morphological and evolutionary issues connected with bars and spirals in galaxies. Although related morphologically, bars are often considered as major dynamical components of galaxies, while spirals are seen as features possibly driven by bars (e.g., Kormendy 1979; Kormendy & Norman 1979). Even so, a significant fraction of normal galaxies are unbarred and still spiral. The role of bars and spirals in secular evolution of galaxies is clearly important.

Barred galaxies can be considered `the ultimate' in galaxy morphology, by which I mean they have some of the most organised structures known. This is shown by the examples in Fig. 21. In these galaxies the bar is obviously a major perturbation, and one of the first questions we may ask is, how many galaxies are barred? A large number of studies have examined this question, often focussing on infrared observations since these penetrate dust and make some obscured bars more visible. One such study by Eskridge et al. (2000) found the following: from H-band (1.65 μm) images of 186 bright nearby galaxies, 56% were visually classified as `strongly barred', 16% were classified as `weakly barred', and 27% were `unbarred'. Although it seems that strong bars are more common than weak ones, this is an illusion. An optically classified SA galaxy may show a weak bar in the IR and get a new classification of SAB, and an optically classified SAB galaxy may show a more prominent bar in the IR and get classified as SB. However, even though the bar of an optically classified SB galaxy may also look stronger in the IR, it has no new classification bin to be placed in. Thus, IR imaging does not really change the rankings of bars. All bars in spirals at least look stronger in the IR, and the rankings (what is actually strong and what is actually weak) remain about the same. From many studies (see Buta et al. 2010b for a recent summary), and including both SAB and SB types, the bar fraction ranges from 50-70%.

Figure 21. The bars in these galaxies are stronger than average and each shows characteristics, such as the presence of a `pseudobulge', that suggest secular evolution has occurred.

Bars are characterised by their different morphologies and non-elliptical shapes. A typical normal bar in an early-type galaxy has two sections: a broad inner zone, and narrower ends (e.g., NGC 4314 in Fig. 22). The inner zone can be round or elliptical and can be mistaken for a large bulge. The broad section is not seen in late-type galaxies generally (e.g., NGC 4731 in Fig. 22). Athanassoula et al. (1990) fitted generalised ellipses to the isophotal shapes of early-type galaxy bars and demonstrated the typical boxy character of these features. In early-to-intermediate-type galaxies, bars are made of an old stellar population, while in very late-type galaxies, bars can include a much younger stellar population. These characteristics are well shown by the examples in Fig. 22.

Figure 22. NGC 4314 shows the characteristic features of an early-type galaxy bar, including the broad inner zone and the boxy narrow ends, while NGC 4731 shows a typical late-type galaxy bar which lacks a broad zone and has a much younger stellar population.

In an ansae-type bar, the broad inner zone and the bar ends may be separated or at least more distinct (Fig. 23). Ansae bars are found in 40% of early-type barred galaxies (Martínez-Valpuesta et al. 2007) and are very rare in later types. Even so, exceptional examples of ansae in intermediate-type spirals are known, such as the SBb galaxy NGC 5375 shown in the upper left frame of Fig. 23. Particularly intriguing, and not really well understood, is the variety of ansae morphologies seen in early-type barred galaxies. Some are roundish spots, others are relatively linear enhancements, while still others are narrow arcs that appear to blend into an inner ring or lens. In colour SDSS images or colour index maps like that shown for NGC 7098 in Fig. 23, ansae are seen to be made of old stars, although NGC 4151 provides a counter example where the ansae are blue and irregular due to star formation.

Figure 23. Colour SDSS images of three galaxies with ansae-type bars, and a colour index map of one, that shows how ansae are often made of an old stellar population but can include young stars, as in NGC 4151. The B - I colour index map of NGC 7098 is coded such that bluer features are dark and redder features are light.

What are the three-dimensional shapes of ansae? The galaxy NGC 4216 (Fig. 24) shows a boxy bulge with bright enhancements that look like ansae in a 3.6 μm image. If this is what the enhancements are, then it appears that ansae are flatter than the inner sections of bars.

Figure 24. In this 3.6 μm image, the nearly edge-on Sb spiral NGC 4216 shows likely ansae (arrows) flanking an inner boxy zone.

The appearance of ansae, and the existence of many bars which do not have them, suggests a possible interpretation of the features in terms of secular evolution (Fig. 25). We can ask: are ansae bars merely a distinct type of bar, related to some aspect of bar formation, or is there a process that changes a normal bar (e.g., as in NGC 4608) into an ansae bar (e.g., as in NGC 2859)? Can this process separate the two parts of a normal bar and eventually stretch the ansae into arcs?

Figure 25. Possible scenario of secular evolution where a full bar evolves to where the broad inner zone and the ends separate.

Ovals are broad, bar-like features having little Fourier amplitude above m = 2, as shown by the example in Fig. 26. Other examples are illustrated by KK04 and B13. The effect of an oval on galaxy morphology can be similar to that of a conventional bar (KK04). The similarity between some oval galaxies and SB galaxies with outer rings suggests that the oval is driving ring formation in the same manner as a bar would. The oval is a bar-like feature sitting in the same place where a bar and an inner ring would be. When a bar or an oval is viewed at an angle intermediate between end-on and broadside on, the isovelocity contours bend towards the bar as in NGC 6300 (Buta 1987). Similar bending can be used to identify an oval in an inclined galaxy (KK04).

Figure 26. Deprojected blue light image of NGC 4941, an outer-ringed galaxy with a prominent inner oval disk.

Boxy or X-morphologies (Fig. 27) are commonly seen in edge-on disk galaxies. Considerable evidence supports the idea that these features are simply the projections of the vertical structure of bars (Bureau & Freeman 1999; Bureau & Athanassoula 1999; Athanassoula & Bureau 1999). However, X-morphologies can also be seen in galaxies inclined less than 50°, e.g., IC 5240 (Buta et al. 2007, see Fig. 27, lower right) and IC 4290 (Buta & Crocker 1991). In such cases, the boxy/X-morphology affects only the broad inner section and not the narrower ends, another argument in favour of the ends of bars being flatter than their middle sections.

Figure 27. Examples of edge-on and non-edge-on X-galaxies.

Barred galaxies are well-known for their ring morphologies. The bar usually fills one dimension of an inner ring, as in NGC 2523 and NGC 1398 (Fig. 28). The inner ring of NGC 1398 especially shows a tight spiral morphology that is mostly distinct from the rest of the galaxy's extensive spiral structure.

Figure 28. NGC 2523 and NGC 1398, two galaxies with conspicuous inner rings.

Outer rings (R) are usually about 2-2.5 times the size of an inner ring/bar. Usually there is only one (R), but very rare cases have two (Fig. 29). The stellar populations in outer rings are potentially very interesting. In NGC 2273, the two outer rings are smooth and both may be characterised mostly by an older stellar population. However, the double outer ring in NGC 1211 has a population dichotomy that is well shown in an SDSS colour image (Fig. 30). The outer outer ring is blue while the inner outer ring, the inner ring, the bar, and the bulge are defined by a much older and redder stellar population. The suggestion is that the outer outer ring is a recent acquisition, possibly an accretion feature where the material from a disrupted companion has settled into the disk plane of a host (R)SB(rl)0⁺ galaxy. Alternatively, NGC 1211's outer structure may be related to what Buta (1995) referred to as an `R₁R'₂' morphology, or double outer ring/pseudoring (Buta et al. 2007). These also can show a population dichotomy with the R₁ component being redder and made of older stars than the R'₂ component. This kind of morphology has been linked to the outer Lindblad resonance, and is described further later in this lecture.

Figure 29. Two galaxies with conspicuous outer rings.

Figure 30. NGC 1211, a double outer-ringed galaxy with an obvious stellar population dichotomy.

The outer spirals in barred galaxies often have variable pitch angle and close into what de Vaucouleurs referred to as an outer pseudoring, (R'). These features are most common among early- to intermediate-type spirals (Buta & Combes 1996). The morphologies of these features are distinctive enough to merit special attention, as shown by the R₁R'₂ morphology. This is also discussed later in this lecture.

Rings are likely products of secular evolution in galaxies, in the following sense. As reviewed by Buta & Combes (1996), the best interpretation of barred galaxy rings is that they form by gas accumulation at resonances, under the continuous action of gravity torques due to the bar. In the presence of a bar potential, gas clouds try and settle into the parent orbits of the potential, but cannot do so without crossing other orbits. This leads to a spiral that slowly can be torqued into rings near orbital resonances (Schwarz 1981, 1984a).

The resonance idea is not the only interpretation of barred galaxy rings that has been put forward (see summary in B13 and also Athanassoula, this volume), but it makes a number of predictions with respect to morphology that are easily testable. To do so, we need to find a reliable way to judge the intrinsic shapes and orientations of inner and outer rings. The way this can be done is to obtain distributions of apparent axis ratios and relative bar-ring position angles, and then to model these distributions under the assumptions of random orientations of the disk planes and zero vertical thickness. The latter assumption is not unreasonable given that rings in spirals are often zones of active star formation.

The Catalogue of Southern Ringed Galaxies (CSRG, Buta 1995) was designed to evaluate the intrinsic shapes and orientations of inner and outer rings in this manner. Inner SB rings are oval with intrinsic axis ratio < q_o > = 0.81 ± 0.06 and are aligned parallel to the bar (Fig. 31, left panel). The velocity field of the nearby galaxy NGC 1433 (Buta et al. 2001) beautifully demonstrates this characteristic alignment. The large inner ring in this galaxy has q_o = 0.63, much more elongated than average. The velocity field betrays this shape by a kinematic line of nodes that is nearly along the minor axis of the ring. Bars may also underfill an inner ring or pseudoring, as in NGC 7098 (Fig. 31, right panel). Bars generally do not overfill inner rings, making H. Curtis's `ϕ-type' characterisation not quite appropriate.

Although parallel alignment is clearly the `rule' for SB inner rings, misalignments are sometimes seen. These are recognised in nearly face-on galaxies as clear cases of inner pseudorings crossed at a large angle by a bar. A kinematically confirmed example is ESO 565-11 (Fig. 31, middle panel; see Buta et al. 1995a). Other likely examples are NGC 309 (Sandage 1961) and CSRG 1052 (Buta 1995).

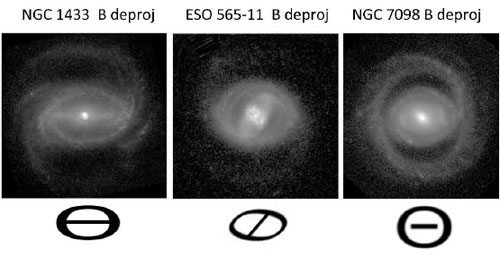Figure 31. Intrinsic inner ring shapes and orientations in barred galaxies.

ESO 565-11 is such an extreme case that it suggests a possible evolutionary effect. The galaxy is not only a misaligned bar-inner ring system, but also a misaligned bar-oval system, because the inner pseudoring lies around the rim of a massive oval, from which stellar outer arms emerge. Since long-term, stable misalignment of massive nonaxisymmetric components is unlikely, the suggestion is that the bar of ESO 565-11 is relatively new, and that it formed within a pre-existing oval that itself is a remnant of a past bar episode. Evidence in support of this idea is the presence of the large and very unusual nuclear ring (Buta et al. 1999). The extreme elongated shape and size of this feature (more than 3 kpc in radius) are likely indicators of its youth.

For SB outer rings/pseudorings, statistics favor < q_o > = 0.82 ± 0.07 and both parallel and perpendicular alignments (Buta 1995). The different alignments are shown with deprojected inner rings in Fig. 32. In each, note the exclusive parallel alignment of the inner rings in the same galaxies.

Figure 32. Intrinsic outer ring and pseudoring shapes and orientations in barred galaxies, as compared with deprojected images.

Nuclear rings (nr) are found well inside bars (Fig. 33). Nuclear rings average 1.5 kpc in diameter, and have roughly circular intrinsic shapes and a morphology that can be shaped by dust. According to Knapen (2005) and Comerón et al. (2010) nuclear rings are found in 20% of galaxies in the type range S0^- to Sd. Figure 34 shows two results from Comerón et al. (2010): that nuclear rings have a wide range of linear diameters, from 200 pc to several kpc, and that stronger bars tend to host smaller nuclear rings, while weaker bars can host small and large rings. The connections between bars and the properties of nuclear rings are discussed further in Knapen (2010).

Figure 33. Two barred galaxies with nuclear rings.

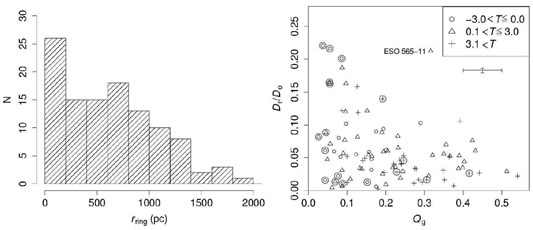Figure 34. Two graphs from Comerón et al. (2010, reproduced with permission) showing the wide range of linear sizes of nuclear rings and the sensitivity of relative ring size to relative bar torque strength Qg.

Found in the same area as nuclear rings are nuclear (secondary) bars (nb) (Fig. 35). According to Erwin (2004, 2011), double bars are found in ~ 20% of S0-Sb galaxies. The sense of a nuclear bar, tipped ahead of (leading) or behind (trailing) a primary bar can be judged from the sense of winding of spiral arms (assumed to be trailing). The existence of both types of nuclear bars argue that these features have a different pattern speed from the primary bar. Erwin (2004, 2011) shows that alignments between nuclear and primary bars are random (Fig. 36), and Corsini et al. (2003) find direct kinematic evidence for it in NGC 2950.

Figure 35. Two barred galaxies with secondary or nuclear bars. The one in NGC 6782 is tipped behind the primary bar and is called trailing, while the one in NGC 1291 is tipped ahead and called leading. Schematics are from Buta & Crocker (1993a).

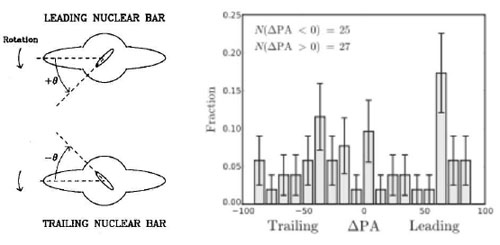Figure 36. The schematic at left shows the definitions of the terms `leading' and `trailing' as applied to nuclear bars in terms of the sign of the angle θ (Buta & Crocker 1993a). The graph at right shows the distribution of θ values for a large sample of secondary bars from Erwin (2004, reproduced with permission).

In terms of secular evolution, nuclear rings are in a different domain from inner and outer rings. Outer rings are thought to have a long timescale (requiring more than a few Gyr to form; Schwarz 1981; Rautiainen & Salo 2000), while nuclear rings, being much closer to the centre, have a timescale of only a few times 10⁸ years (Combes 1991). Only nuclear rings are prone to extreme bursts of star formation. The presence of a nuclear bar inside a star-forming nuclear ring (as, e.g., in NGC 6782) should produce gravity torques that could evolve the central regions (Shlosman et al. 1989). Also, the coexistence of nuclear, inner, and outer rings, each with a very different time scale, in the same galaxy, suggests a persistent means of funnelling gas towards the central regions.

5.1. Quantifying bar strength

One of the major goals de Vaucouleurs had during his long career was to find ways of quantifying the three dimensions of the VRHS. He imagined setting the stage T = f (colour, surface brightness, Hi content, etc.), where f is a numerical function of measured parameters, each of which correlate individually with stage but with a large scatter. However, no effective way of doing this was ever really found. T is still best estimated visually. In contrast, there is more than one way of reliably quantifying bars. Doing this would be useful for several reasons: (1) to judge the actual significance of a bar within its disk; (2) to examine the connection between bars and spirals (e.g., we can ask: do the former `drive' the latter?); and (3) to investigate how measureable properties of bar-associated features like rings correlate with bar strength.

Relative Fourier intensity amplitudes can quantify the light perturbation effectively. Two examples involving early-type barred galaxies are shown in Fig. 37. A₂ is the maximum of the relative m = 2 Fourier amplitude I₂ / I₀. The amplitudes are derived from a Fourier expansion of the brightness distribution:

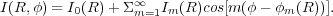(1)

With such an expansion, the sine and cosine amplitudes are derived as

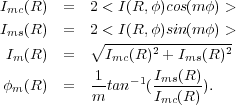(2)

An important finding from Buta et al. (2006) is the single and double Gaussian forms of the radial variations of I_m / I₀ for some galaxies, especially early-types. The solid curves fitted to the amplitudes of the two early-type examples (Fig. 37) shows how well these representations work. The physical significance of these forms is unclear; however, similar forms have been seen in numerical simulations. For example, the relative Fourier profile for NGC 1452 is similar to a `massive halo' bar model from Athanassoula & Misiriotis (2002). Note that more complex Fourier profiles are seen that can be described as multi-Gaussian in nature, often occurring when the bar is embedded in a massive oval.

Interestingly, single Gaussian bars are not restricted to early types like NGC 1533. The same kind of bar is seen in the SBb spiral NGC 3351. Figure 37, right, shows m = 2 and 4 Fourier profiles and their Gaussian representations for NGC 3351. Also shown is how effectively this representation removes the bar from an infrared image of the galaxy. Single Gaussian bars appear to be the simplest type, but remain to be explained.

Figure 37. Examples of single and double-Gaussian Fourier bar profiles. (Left frames): m = 2, 4, and 6 Ks-band relative Fourier intensity profiles and B-band images of early-type galaxies NGC 1452 and NGC 1533 (Buta et al. 2006). (Right frames): 3.6 μm Fourier profiles and images of NGC 3351, showing that a single Gaussian fits the m = 2 and 4 Fourier profiles well.

5.2. Bar strength from maximum relative gravitational torques

Another way of quantifying bar strength is to use an infrared image to trace stellar mass and infer the gravitational potential Φ. Then the bar strength can be estimated in terms of the maximum relative tangential forcing. Using Fast Fourier Transform techniques (Binney & Tremaine 1987, Section 2.9), a two-dimensional image may be converted to a two-dimensional potential on a Cartesian grid (Quillen et al. 1994). From this potential we derive the parameter

(3)

where F_T = (1 / R) (∂Φ / ∂ϕ) is the tangential force and F_0R = ∂Φ₀ / ∂ R is the mean radial force. This approach follows Sanders & Tubbs (1980) and Combes & Sanders (1981).

The actual application of this method is described by Buta et al. (2007) and highlighted in Fig. 38. Force ratio maps yield a `butterfly' pattern defined by four `islands' of high tangential forcing. Following the maximum of F_T / F_0R through each quadrant (dotted curves, lower left of Fig. 38), and then averaging over the four quadrants, gives a curve like that in the right panel of Fig. 38. For the actual bar strength, we take the maximum of the average maxima, called Q_g. Strictly speaking, Q_g is the bar strength only if there are no other perturbing features besides a bar, such as spiral arms. If arms are present, then Q_g can include contributions from these as well. Buta et al. (2003) describe a Fourier-based method of separating a bar from the surrounding spiral. This allows the true bar strength Q_b to be estimated, as well as an estimate of the spiral strength Q_s. In general, if the bar is strong compared to the spiral, then Q_b ≈ Q_g, while if the spiral is stronger than the bar, then Q_s ≈ Q_g.

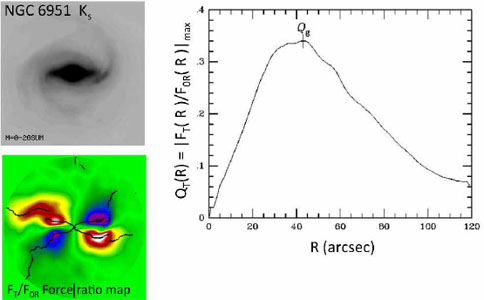Figure 38. Derivation of Qg for NGC 6951, from Buta et al. (2003).

With these caveats in mind, let us examine how the strengths of spiral patterns correlate with bar strength. It is well-known that the spiral patterns in barred galaxies are generally global in nature (Kormendy & Norman 1979). Rare examples have flocculent spirals instead. Figure 39 shows several examples. An important question is, do the bars themselves `drive' these patterns, or are the spirals mostly independent instabilities? In an article titled `Do bars drive spiral density waves?', Buta et al. (2009) compared maximum relative spiral and bar torque strengths and detected a weak positive correlation. In a follow-up paper `Bars do drive spiral density waves', Salo et al. (2010) compared local relative spiral and bar torque strengths and found a much better correlation, confirming the conclusion of Kormendy & Norman (1979). This does not mean that all the spirals in barred galaxies are necessarily driven by the bar. As will be described in Lecture 3 (see Section 6), potential-density phase shift studies suggest that some spirals are decoupled from their bars.

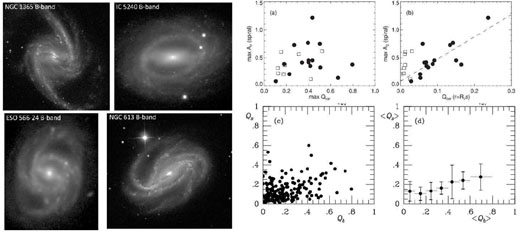Figure 39. Examples of global SB spirals (left) and correlations of bar and spiral strength from Buta et al. (2009, bottom-right panels) and Salo et al. (2010, upper-right panels).

5.3. Inner ring shapes and bar strength

As described previously, inner SB rings have a mean intrinsic axis ratio of q_o = 0.81 ± 0.06. However, individual cases suggest that inner rings can have a shape over the much broader range q_o = 0.6-1.0 (Buta 1986). Another question we can ask is: do inner ring shapes correlate with bar strength? Theoretically, such a correlation should exist because bar strength can determine the shapes of periodic orbits, and rings are thought to take on the shapes of specific orbits (e.g., Schwarz 1984b; Rautiainen & Salo 2000).

It is an interesting aspect of SB inner rings that the way Hii regions are distributed around the rings is sensitive to intrinsic ring shape but not to maximum relative bar torque strength Q_g (Buta 2002; Buta et al. 2007). Nearly circular inner rings may be found around strong bars just as highly elongated rings are found. However, if you compare the ring radius with the radius of the bar torque maximum, then a correlation is found. Figure 40 shows that a highly elongated inner ring is found when the semi-major axis radius of the ring a_r ≈ R(Q_g), the radius of the relative bar torque maximum. In such a case, the ring essentially lies on the bar and can be considered a part of the bar. Hii regions are seen to `bunch up' around the ends of the bar, as in NGC 6782. In contrast, when a_r > R(Q_g), the bar maximum is far enough inside the ring radius to allow the ring to be more circular, as in NGC 53. In this case, the Hii regions are distributed more uniformly around the ring.

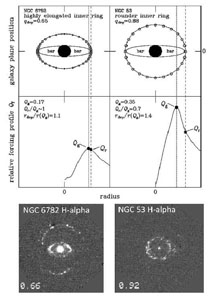Figure 40. How inner ring shape connects to bar torque strength. The Hα images are from Crocker et al. (1996) while the schematics are from Grouchy et al. (2010).

None of this really explains why some galaxies select one possible ring orbit over another. According to Schwarz (1984b), an inner ring takes on the shape of the largest 4:1 resonant orbit that is not cusped and which does not cross another orbit. However, simulated inner rings could have more diamond-like shapes if higher-order Fourier harmonics in the bar were important. Such a shape seems present in the inner ring of NGC 6782, and indeed Lin et al. (2008) interpreted the shape of this galaxy's inner ring in terms of an interaction between waves excited at the inner 4:1 resonance and waves excited at the inner Lindblad resonance, based on hydrodynamical simulations. These authors also attributed the distribution of Hii regions around the bar ends as due to an interaction between the gas and curved shocks.

It is unclear how the shapes of inner rings might evolve over time. The likely evolution is from a pseudoring to a ring, while a change in ring shape might link more to changes in the bar pattern speed, which affects the actual location of resonances as I now describe. In a model galaxy having a significant halo and a moderately rising rotation curve, Rautiainen & Salo (2000) found a time sequence where a highly elongated inner ring becomes more circular.

5.4. Resonances in barred galaxies

The presence of even a weak bar sets up a pattern speed Ω_p and resonances in a differentially rotating disk. A perturbed orbit in a weak bar potential has this shape (Binney & Tremaine 2008):

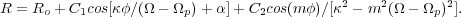(4)

The resonances are in the C₂ terms and are as follows:

1. Corotation resonance (CR): Ω = Ω_p

2. Inner Lindblad resonance (ILR): Ω - Ω_p = κ / 2

3. Outer Lindblad resonance (OLR): Ω - Ω_p = -κ / 2

4. Inner 4:1 resonance (I4R): Ω - Ω_p = κ / 4

5. Outer 4:1 resonance (O4R): Ω - Ω_p = -κ / 4

where κ = 2Ω[1 + (1/2) (R / Ω) (dΩ / dR)]^1/2 is the epicyclic frequency and Ω is the circular angular velocity.

Are these resonances detectable in real galaxies? The answer is yes, and a variety of methods is available to detect them in both barred and spiral galaxies. Here we are mainly interested in how these resonances might be manifested morphologically, and what their long-term impact on morphology might be.

The most direct method of locating resonances is to apply the Tremaine-Weinberg (1984) approach, which uses the equation of continuity to estimate the pattern speed Ω_p. Along a set of slits oriented parallel to the major axis (Fig. 41, left), one derives the luminosity-weighted averages of the line of sight velocity <V> and the position <X>. A graph of <V> versus <X> has the slope Ω_psini, where i is the inclination. Then the CR is located by using a rotation curve to calculate how Ω varies with galactocentric radius. The method has been mostly applied to SB0 galaxies to derive the parameter , where = R_CR / R_bar. The results have suggested that most bars in SB0 galaxies are fast with ≈ 1-1.4 (Corsini 2011; Fig. 41, right).

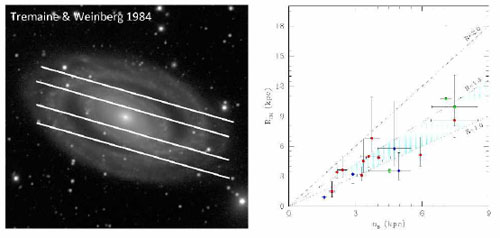Figure 41. (Left): NGC 7098 with a set of parallel slits along the major axis set up to estimate the pattern speed using the Tremaine-Weinberg method. (Right): graph from Corsini (2011) showing the preponderance of fast bars in a sample of mostly SB0 galaxies. Reproduced with permission.

5.5. Rings and pseudorings as tracers of the bar pattern speed

Rings were tied early on to resonances in galaxies harbouring density waves. Many rings are zones of active star formation, and in colour index maps all ring types, inner, outer, and nuclear, can show enhanced blue colours (e.g., NGC 3081, Buta & Purcell 1998).

Schwarz (1981) made test-particle simulations of barred galaxies that led to the recognition of two morphologies that should be observed near the OLR. The first type involves outer arms that wind 180° and close into a pseudoring aligned perpendicular to the bar, while the second type has arms winding 270° and is aligned parallel to the bar. Within the limitations of Schwarz's models, the first type was favoured if there was little gas outside the OLR, while the second was favoured if there was more gas outside the OLR. These types were searched for and found by Buta (1985, 1995), who called the first type R'₁ and the second type R'₂, implying these should be interpreted as outer pseudorings. The argument that these features trace the OLR was strengthened by the identification of galaxies showing a combination of these two types, called R₁R'₂ by Buta (1995). In these types, you can almost see the two families of OLR periodic orbits that Schwarz linked to the two main types originally. The Catalogue of Southern Ringed Galaxies (Buta 1995) includes many examples of all three categories, and many others can be found in the GalaxyZoo database (www.galaxyzoo.org forums). Figure 42 shows schematics of what are known as the `OLR subclasses', while many examples are shown in Fig. 42, right, and the dVA.

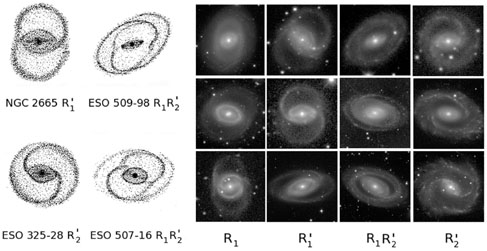Figure 42. Schematics of OLR morphologies and examples (from B13).

Schwarz (1981) did not predict the existence of the R₁R'₂ morphology. How it might develop was shown by Byrd et al. (1994) in modified Schwarz-type simulations. These showed an evolution from R₁ to R'₂, and that an R₁R'₂ morphology develops mainly in cases where the pattern speed is relatively high and no inner resonances occur (Fig. 43). The more sophisticated N-body models of Rautiainen & Salo (2000) found an almost cyclic change between R₁ and R₂ morphologies, due to the presence of a slower spiral mode in the outer disk. These authors also explained the absence of rings as being due either to the non-existence of a required resonance (like ILR) or, even when a resonance (like OLR) existed, to the greatly differing timescales of the different ring types.

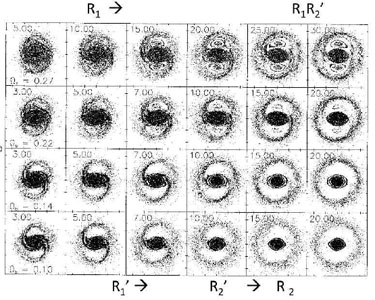Figure 43. High pattern speed simulations of barred galaxies from Byrd et al. (1994), showing the evolution of ring and pseudoring patterns at the OLR.

The intrinsic shapes and orientations of rings also favour identification of rings with resonances. In the simulations of Simkin et al. (1980), a highly elongated inner ring aligned parallel to the bar forms at the inner 4:1 ultraharmonic resonance (I4R). This and the two alignments of outer pseudorings are consistent with CSRG statistics.

Up to four resonant ring features may be present in the same galaxy. Example: the remarkable `resonance ring galaxy' NGC 3081 (Buta et al. 2004). Recognising all of its rings and a nuclear bar as well, here is a revised type for NGC 3081: (R₁R'₂)SAB(r,nr,nb)0/a.

Can we use the rings in NGC 3081 to estimate the pattern speed? Using a Fabry-Perot velocity field and a representation of the rotation curve, Buta & Purcell (1998) derived Ω and the precession frequencies Ω ± κ/2 and Ω - κ/4 and set the OLR between the R₁ and R'₂ features. The resulting value of Ω_p placed the inner ring near the I4R and the nuclear ring between two ILRs, consistent with the findings of Schwarz (1984a) and Simkin et al. (1980). Figure 44 shows how well NGC 3081 fits into barred spiral theory. The images show the deprojected galaxy after subtraction of an exponential disk model. If the R₁R'₂ feature locates the OLR, then CR lies in the `gap' between the inner ring and the R₁ outer ring.

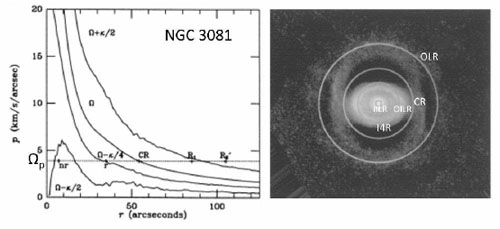Figure 44. (Left): Precession frequency curves for NGC 3081. (Right): Resonance locations from rotation curve analysis (Buta & Purcell 1998).

A particularly interesting case with possible resonant features is the galaxy NGC 1433, which has an exceptionally well-defined and unusually highly elongated inner ring (dVA). In addition, the galaxy has two secondary spiral arcs off the leading sides of the bar called `plumes' by Buta (1984). Treuthardt et al. (2008) were able to simulate both the inner ring and the plumes, as well as the outer R'₁ pseudoring using a near-IR image to define the potential. These simulations demonstrated that the outer pseudoring in this case is likely related to the outer 4:1 resonance (O4R), not the OLR as would have been expected from Schwarz's simulations. A similar result was deduced for the outer R₁ ring of NGC 6782 by Lin et al. (2008).

As important as the `OLR subclasses' are for understanding galaxy structure, there has been no systematic study of the global properties of these galaxies and how their structure (e.g., disk scalelengths, bulge-to-total luminosity ratios, etc.) compare with galaxies that lack these features. Interestingly, Pérez et al. (2012) have used R'₂ pseudorings to examine the evolution of bar pattern speeds.

The possible evolution of nuclear rings might be evident in their observed colours. Figure 45, left, shows optical and near-IR images and colour index maps of NGC 1512, an early-type barred galaxy that harbours both inner and nuclear rings. The nuclear ring in NGC 1512 is blue in a B - I colour index map because of large numbers of young blue supergiants. However, the ring is `red' in a J - K_s colour index map, implying the likely presence of a large number of young red supergiants as well. In contrast, the nuclear ring of NGC 3081 is also blue in a B - I colour index map (Buta & Purcell 1998) but is largely invisible in a J - K_s map (Fig. 45, right), implying far fewer red supergiants (and probably a more evolved ring than the one in NGC 1512).

Figure 45. Optical and near-IR colours of nuclear rings.

5.6. Are bars generally slightly skewed?

The final morphological question I want to ask about bars is, how straight are they? There is some indication that bars can be skewed in the form of very open spirals. In the SDSS galaxy shown in Fig. 46, the bar is skewed trailing, while in NGC 4596 in the same figure, the bar is slightly skewed leading, both after assuming trailing outer arms. The incidence and amplitude of bar skewness has not been determined, but some interesting cases have been identified. As shown in Fig. 46, the bar of NGC 3124 is distinctly skewed in a leading sense with little ambiguity. Bar skewness can lead to secular evolution by the potential-density phase shift that would result (Zhang 1996). This is described further in Lecture 3 (see Section 6).

Figure 46. Examples of skewed bars. The SDSS galaxy at left was selected from the GalaxyZoo Forum but its identity was not posted. The image of NGC 4596 is deprojected to face-on and the superposed curve shows the phase of the m = 2 component. At right is NGC 3124, as it appears in an I-band image and an m = 2 Fourier image.

5.7. Secular evolution in barred galaxies

The general view of secular evolution in barred galaxies is that the main effect is the ability of a bar to drive interstellar gas into the centres of galaxies, fuelling star formation and building up a pseudobulge (KK04). Figure 47 shows all of the types of features considered to be pseudobulges by KK04 as compared to `classical' (merger-built) bulges. Pseudobulges include not only `disky bulges' (as they are called by Athanassoula 2005; see top row of examples), but also nuclear bars and boxy-bulge galaxies. Pseudobulges generally have a low Sérsic index (see Lecture 3, Section 6), are flatter, and have a higher ratio of rotation to random motions compared to classical bulges.

Figure 47. Examples of pseudobulges and classical bulges. From B13 based on KK04.

1. Can a `normal' bar separate its middle section from its ends? Why would it do this? This is more a question of how ansae form and what they mean to galactic dynamics. If S0 galaxies are stripped or otherwise gas-depleted former spirals, and at the same time have a very different distribution of bar strengths from spirals, then bar evolution is a possible avenue to explore for the origin of ansae.

2. What causes intrinsic bar-ring misalignment? Is this a phase in bar evolution? This is such a rare phenomenon that it is likely to be relatively short-lived. Nevertheless, bar-ring misalignment (which can also mean bar-oval misalignment) could point to an evolutionary mechanism: the destruction and rejuvenation of bars. If destruction of a bar can lead to formation of a lens-oval, and then external gas accretion cools the disk enough for bar rejuvenation, could the new bar have a different pattern speed from the old one? The misalignment between primary and secondary bars has also been attributed to different pattern speeds (e.g., Buta & Crocker 1993a).

3. Why would a bar be skewed in a leading sense? I have shown that there are suggestive examples where a bar is curved like a very open spiral. When the mass associated with such spirals is converted into a gravitational potential, a small phase difference can result that has relevance to secular evolution (Lecture 3, Section 6). But what is determining the sense of spirality of the bar? Bar skewness supports the idea that a bar is a density wave like an ordinary spiral.

4. What do double outer rings mean? Why should one ring be red and the other blue? Double outer rings seem much less common than double outer rings/pseudorings. The latter is usually found as the R₁R'₂ morphology. But cases classified as `(RR)' as in the dVA (example: NGC 2273) are very rare. Could a double outer ring signify two episodes of ring formation at different values of the pattern speed?

5. Is there an evolutionary connection between R₁ and R₂ outer rings? Did detached outer rings begin as pseudorings? The simulations of Byrd et al. (1994) showed a clear trend of evolution from an R'₁ to an R'₂ outer pseudoring, followed by a detached outer ring. At high pattern speeds, an R₁R'₂ morphology developed. Rautiainen & Salo (2000) suggested a different evolutionary connection, in that the presence of a slower spiral mode in the outer disk would cause cyclic changes from R₁ to R₂.