Modern observational cosmology relies on combining multiple observations to make inferences about the correct cosmological model. It uses Bayes theorem to do this. Suppose we have a hypothesis to be tested H, a set of things assumed to be true I (for example the model of the observations), and a set of data d, then Bayes theorem gives that
 |
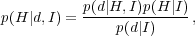(47) |
where L(H) ≡ p(d|H,I) is the sampling distribution of data, often called the Likelihood, p(H|I) is the prior, p(d|I) the normalisation, and p(H|d,I) the posterior probability.
The hypothesis to be tested is often a vector of parameters
,
which can be split into interesting
(e.g. the
dark energy equation of state w(z)), and uninteresting
(e.g. the
parameters of the smooth fit to the broad-band power when extracting
the BAO signal) parameters. Parameter inference is performed as
 |
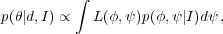(48) |
in order to marginalise over the nuisance parameters, while retaining information about the interesting parameters. Often we wish to know the probability distribution for each parameter in turn having marginalised over all others.
The primary concern when making parameter inferences is keeping a handle on the physics that is being used, and allowing for all of the potential sources of systematic error. When multiple data sets are combined it becomes difficult to follow systematics through the procedure, or to understand which parts of the constraints are coming from which data set. In addition, a prior is required for the hypothesis, whose impact can sometime be large, such that constraints come from this, rather than the data.
6.1. Exploring parameter space
Often, the list of parameters is long, and thus multi-parameter likelihood calculations would be computationally expensive using grid-based techniques. Consequently, fast methods to explore parameter spaces are popular, particularly the Markov-Chain Monte-Carlo (MCMC) technique, which is commonly used for such analyses. While there is publicly available code to calculate cosmological model constraints (Lewis and Bridle 2002), the basic method is extremely simple and relatively straightforward to code.
The MCMC method provides a mechanism to generate a random sequence of parameter values whose distribution matches the posterior probability distribution. These sequences of parameter, or "chains" are commonly generated by an algorithm called the Metropolis algorithm (Metropolis et al. 1953): given a chain at position x, a candidate point xp is chosen at random from a proposal distribution f(xp|x) - usually by means of a random number generator tuned to this proposal distribution. This point is always accepted, and the chain moves to point xp, if the new position has a higher likelihood. If the new position xp is less likely than x, then we must draw another random variable, this time with uniform density between 0 and 1. xp is accepted, and the chain moves to point xp if the random variable is less than the ratio of the likelihood of xp and the likelihood of x. Otherwise the chain "stays" at x, giving this point extra weight within the sequence. In the limit of an infinite number of steps, the chains will reach a converged distribution where the distribution of chain links are representative of the likelihood hyper-surface, given any symmetric proposal distribution f(xp|x) = f(x|xp) (see, for example, Roberts 1996).
It is common to implement dynamic optimisation of the sampling of the likelihood surface (see other articles in the same volume as [Roberts 1996] for examples), performed in a period of burn-in at the start of the process. One thorny issue is convergence - how do we know when we have sufficiently long chains that we have adequately sampled the posterior probability. A number of tests are available (Gelman and Rubin 1992, Verde et al. 2003), although it's common to also test that the same result is obtained from different chains started at widely separated locations in parameter space.
A lot of the big questions to be faced by future experiments can be
reduced to understanding whether a simple model is correct, or whether
additional parameters (and/or physics) are needed. For example, a lot
of future experiments are being set up to test whether the simple
CDM model is
correct. A model with more parameters will
always fit the data better than a model with less parameters (provided
it replicates the original model), while removing parameters may or
may not have a large impact on the fit. The interesting question is
whether the improvement allowed by having an extra free parameter is
sufficient to show that a parameter is needed? Bayes theorem,
Eq. (47), can test the balance between quality of fit and
the predictive ability, potentially providing an answer to these
problems.
The Bayesian evidence is defined as the average of the Likelihood under the prior, given by p(d|I) in Eq. (47). Splitting into model and parameters,
 |
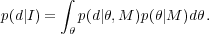(49) |
The Bayes factor is defined as the ratio of the evidence for two models
 |
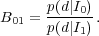(50) |
The strength of the evidence that the Bayes factor gives is often quantified by the Jeffries scale, which requires B01 > 2.5 to give moderate evidence for an additional parameter, and B01 > 5.0 for strong evidence.
One problem with this approach is that the results depends on the prior that is placed on the new parameter. For a wide prior covering regions in parameter space that are unlikely, the average likelihood and Bayes factor are reduced. A tight prior around the best-fit position will lead to an increase in the Bayes factor. Because of this, many variations on this test for new parameters have been proposed (e.g. review by Trotta 2008).