


As defined in the previous section, SBBN refers to BBN in the context of Einstein gravity, with a Friedmann-Lemaître-Robertson-Walker cosmological background. It assumes the Standard Model of nuclear and particle physics, or in other words, the standard set of nuclear and particle interactions and nuclear and particle content. Implicitly, this means a theory with a number Nν = 3 of very light neutrino flavors 1 SBBN also makes the well-justified assumption that during the epoch of nucleosynthesis, the universe was radiation dominated, so that the dominant component of the energy density of the universe can be expressed as
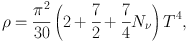 |
(1) |
taking into account the contributions of photons, electrons and positrons, and neutrino flavors appropriate for temperatures T > 1 MeV. At these temperatures, weak interaction rates between neutrons and protons maintain equilibrium.
At lower temperatures, the weak interactions can no longer keep up with the expansion of the universe or equivalently, the mean time for an interaction becomes longer than the age of the Universe. Thus, the freeze-out condition is set by
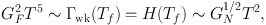 |
(2) |
where Γwk represents the relevant weak interaction rates per baryon that scale roughly as T5, and H is the Hubble parameter
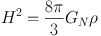 |
(3) |
and scales as T2 in a radiation dominated universe. GF and Gn are the Fermi and Newton constants respectively. Freeze-out occurs when the weak interaction rate falls below the expansion rate, Γwk < H. The β-interactions that control the relative abundances of neutrons and protons freeze out at Tf ∼ 0.8 MeV. At freeze-out, the neutron-to-proton ratio is given approximately by the Boltzmann factor, (n/p)f ≃ e−Δ m/Tf ∼ 1/5, where Δ m = mn−mp is the neutron–proton mass difference. After freeze-out, free neutron decays drop the ratio slightly to (n / p)bbn ≃ 1/7 before nucleosynthesis begins. A useful semi-analytic description of freeze-out can be found in [58, 59].
The first link in the nucleosynthetic chain is p + n → d + γ and although the binding energy of deuterium is relatively small, Eb = 2.2 MeV, the large number of photons relative to nucleons, η−1 ∼ 109 causes the so-called deuterium bottleneck. BBN is delayed until η−1 exp(−Eb / T) ∼ 1 when the deuterium destruction rate finally falls below its production rate. This occurs when the temperature is approximately T ∼ Eb / lnη−1 ∼ 0.1 MeV.
To a good approximation, almost all of the neutrons present when the deuterium bottleneck breaks end up in 4He. It is therefore very easy to estimate the 4He mass fraction,
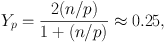 |
(4) |
where we have evaluated Yp using (n / p) ≈ 1/7. The other light elements are produced in significantly smaller abundances, justifying our approximation for the 4He mass fraction. D and 3He are produced at the level of about 10−5 by number, and 7Li at the level of 10−10 by number. A cooling Universe, Coulomb barriers, and the mass gap at A = 8 prevents the production of other isotopes in any significant quantity.
Our BBN results use an updated version of our code [10, 19], itself a descendant of the Wagoner code [60]. For the weak n ↔ p interconversion rates, the code calculates the 1-D phase space integrals at tree level; this corresponds to the assumption that the nucleon remains at rest. The weak n↔ p interconversion rates are normalized such that we recover the adopted mean neutron lifetime at low temperature and density. To this we added order-α radiative and bremsstrahlung QED corrections, and included Coulomb corrections for reactions with p e− in the initial or final states [61]. We neglected additional corrections, because the overall contribution of all other effects is relatively insignificant. Finite temperature radiative corrections leads to Δ Yp ∼ 0.0004; corrections to electron mass leads to Δ Yp ∼ -0.0001; neutrino heating due to e+e− annihilation leads to Δ Yp ∼ 0.0002 [61]. Problems in the original code due to the choice of time-steps in the numerical integration [62] have been corrected here. Finally, we included the effects of finite nucleon mass [63] by increasing the final 4He abundance with Δ Yp = + 0.0012. We formally adopt the Particle Data Group's current recommended value [29]: τn = 880.3 ± 1.1 for the mean free neutron decay lifetime, and assume it is normally distributed.
In addition to the weak n ↔ p interconversion rates, BBN relies on well-measured cross sections. The latest update to these reaction rates has been evaluated by the NACRE collaboration and released as NACRE-II [20]. Only charge-induced reactions were considered in NACRE-II, and many more reactions are evaluated there than is relevant for BBN. Those reactions of relevance are shown in Table 1. The compilation presents tables of reaction rates, with recommended “adopted”, “low” and “high” values. We assume the rates are distributed with a log-normal distribution with:
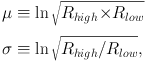 |
(5) (6) |
where Rlow and Rhigh are the recommended “low” and “high” values for the reaction rates, respectively [21]. These rates agree well with previous evaluations [10, 14, 15, 16], largely because they depend on the same experimental data. Uncertainties in the NACRE-II evaluation are similar to, but tend to be larger than previous studies. This may stem from the method used to derive accurate descriptions of the data and the fitting potential models used in Distorted-Wave Born Approximation (DWBA) calculations.
| d(p, γ )3He | d(d, γ )4He | d(d, n)3He |
| d(d, p)t | t(d, n)4He | 3He(d,p)4He |
| d(α ,γ )6Li | 6Li(p, γ)7Be | 6Li(p, α)3He |
| 7Li(p, α)4He | 7Li(p, γ)8Be a |
The remaining relevant n-induced rates, p(n, γ )d, 3He(n, p)t and 7Be(n, p)7Li, need to be taken from different sources. We adopt the evaluation from [64] for the key reaction p(n, γ )d. The remaining (n, p) reactions we use are rates taken from [14]. We choose log-normal parameters in such a way to keep the means and variances of the reaction rates invariant.
As a prelude to the more detailed analysis given below, we first discuss the BBN predictions at a fixed value of η. This benchmark can then be compared to the results of other codes.
Here, we fix η10 ≡ 1010 η = 6.10. This is related to the value of ωb determined by Planck [6] based on a combination of temperature and polarization data 2. The result of our BBN calculation at η10 = 6.10 can be found in Table 2 compared to the fit in [3], based on the PArthENoPE code [4]. As one can see, the results of the two codes are in excellent agreement for all of the light elements. The results can be quickly compared with the observed abundances given in the next section. However a more rigorous treatment of the comparison between theory and observation will be given in section 4.
| η10 | Nν | Yp | D/H | 3He/H | 7Li/H | 6Li/H | |
| This Work | 6.10 | 3 | 0.2470 | 2.579 × 10−5 | 0.9996 × 10−5 | 4.648 × 10−10 | 1.288 × 10−14 |
| Iocco et al. [3] fit | 6.10 | 3 | 0.2463 | 2.578 × 10−5 | 0.9983 × 10−5 | 4.646 × 10−10 | 1.290 × 10−14 |
1 We distinguish between the number of neutrino flavors, three in the Standard Model, and Neff, equal to 3.046 in the Standard Model, which corresponds to the effective number of neutrinos present in the thermal bath due to the higher temperature from e+ e− annihilations before neutrinos are completely decoupled. Back.
2 A straight interpretation of the Planck result based on the TT,TE,EE,+lowP anisotropy data would yield η10 = 6.09. However this result already includes the He abundance from BBN. Our choice of η is discussed in Section 4.3 and Table 4 below. Back.