So far we have only considered the response of the stars in galactic discs, but the response of the gas is important for considering spiral structure. The velocity dispersion in the gas is less than that of the stars, so the gas response to any perturbations in the stellar disc is highly amplified. Thus even small overdensities in the stars can result in clear spiral arms in the gas (for example see the IR maps in Elmegreen (2011) compared to optical images). And furthermore as the gas forms young stars, in the optical we are dominated by the spiral pattern in the gas not the stars. Therefore processes in the gas, and star formation, will have shaped the spiral patterns that we observe.
3.1. Stability of a star and gas disc
As described in Section 2.1, gas or stars in a disc are expected to undergo local axisymmetric gravitational instabilities according to the criteria in Equations 7 and 10. For a disc of stars and gas, local, transient instabilities in the stars are expected to be coupled by a similar response in the gas. Similar to the dispersion relations and stability criteria derived for gas and stars separately, we can also derive similar expressions for a disc of gas and stars. We note that, like in Section 2.1, the derivations here assume the tight winding approximation.
Jog & Solomon (1984) first tackled the problem of a galactic disc of stars and gas, by treating the disc as a two-fluid system. They derived the following dispersion relation
 |
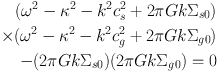(31) |
where cs and cg are the velocity dispersion of the stars and gas respectively, and Σs0 and Σg0 are the surface densities of the stars and gas respectively. Thus the stars and gas are treated as co-existing fluids with different surface densities and velocity dispersions. They also determined a local stability criterion.
Bertin & Romeo (1988) then determined a global stability criteria for a two-fluid disc. They defined a marginal stability curve given by
 |
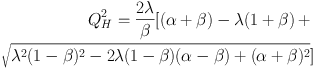(32) |
where λ = kg / |k|, α = ρc / ρh and β = σc2 / σh2, where ρ is density, σ is the radial dispersion, and subscripts c and h represent cold and hot components. Potentially, Qh can exhibit two peaks, one arising from instability in the gas (at smaller wavelengths), and one from the stars (see Figure 3 of Bertin & Romeo, 1988). Stability globally at all wavelengths then requires that Q2, where Q corresponds to the standard criterion (Equation 7) for the hot component, is greater than the maximum of Qh2.
Rafikov (2001) derived the dispersion relation for a disc with a fluid, and a collisionless component (see also Romeo (1992)):
 |
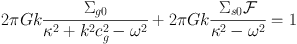(33) |
where 
is defined as for
Equation 9.
Then, for the disc to be stable (requiring ω2(k)
> 0 for all k), he derived the criterion
 |
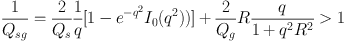(34) |
where
 |
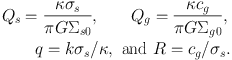Note that Qg is not the same as shown earlier for Equation 7, and this is again a criterion for local instabilities. Wang & Silk (1994) also present a simplified approximate stability criterion, (Qs-1 + Qg-1)-1, with Qs and Qg defined as above.
These equations still do not represent a multiphase medium, and are for a thin disc. Some authors have tried to incorporate a more realistic ISM (Romeo et al., 2010, Romeo & Wiegert, 2011, Romeo & Falstad, 2013), but we do not consider these further here. One of the main results arising from these criteria though is that small changes in the gas can change the stability of the disc significantly, compared to relatively large changes in the stellar component (Jog & Solomon, 1984, Rafikov, 2001).
Following these derivations, Li et al. (2005) investigated the stability criterion of Rafikov (2001) using numerical simulations of an isothermal disc. They found gravitational collapse when Qsg < 1.6, and vigorous star formation when Qsg < 1. With a multiphase medium, gravitational collapse will always occur in a disc of stars and gas with realistic surface densities. Many such simulations have shown the development of dynamic spiral arms simultaneously in the gas and stars, and the formation of molecular clouds and star formation within them (e.g. Robertson & Kravtsov (2008), Hopkins et al. (2011), Wada et al. (2011)).
Large-scale shocks (namely spiral shocks or galactic shocks) are predicted in the gas as the result of spiral density waves (see Section 3.5), or even generic turbulence in the spiral arms, so they are naturally expected to lead to energy dissipation.
By computing the energy change across the shock, and momentum conservation, Kalnajs (1972) showed that the rate of change of energy density of tightly winding quasi-stationary spiral density waves is
 |
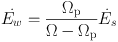(35) |
(see also
Binney
& Tremaine (2008)),
where 
s is
the energy dissipation in the shock and
w is the
energy change in the density wave. The energy dissipation,
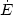s is
negative, hence Ew increases when Ωp
< Ω (i.e., R < RCR) and
decreases when Ωp > Ω (i.e., R >
RCR). By noting that Ew is negative
in the first case, and positive in the second case
(Binney
& Tremaine, 2008),
it is evident that the induced shock always damps the density wave
(Kalnajs, 1972).
The damping timescale, -Ew /
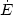w, is
estimated to be between ∼ 108 - 109 yrs
depending on the calculation of the energy terms, and the nature of the
shock
(Kalnajs, 1972,
Roberts &
Shu, 1972,
Toomre, 1977).
Another basic consequence of damping is that in the case of
quasi-stationary spiral density waves,
the streamlines predicted to describe the gas trajectories
(Roberts (1969),
see Section 3.5) will not be closed
(Kalnajs, 1972).
Following this result, a model of self regulated spiral structure was put forward by Bertin & Romeo (1988), also following discussion in Roberts & Shu (1972). Spiral perturbations in the disc are predicted to grow with time (see Section 2.1.4). Hence Bertin & Romeo (1988) proposed that gas damps the spiral perturbations, which are then regenerated on timescales comparable to the damping timescale. They point out that in the absence of gas, the stars would instead continue to heat until the disc becomes stable to spiral perturbations (Lin & Bertin, 1985).
For dynamic spirals, damping was also thought to be important. As mentioned in Section 2.2, early simulations (e.g. Sellwood & Carlberg (1984)) found that stellar discs heated up with time, as supposed in the previous paragraph, and consequently the spiral arms disappear after several galactic rotations. Furthermore, galaxies which have little gas did not appear to have any spiral structure, suggesting that gas damping is always a requisite for spiral structure (Binney & Tremaine, 2008). However, Fujii et al. (2011) and D'Onghia et al. (2013) showed that spiral arms were able to survive much longer (see Section 2.2). Fujii et al. (2011) demonstrated that stellar heating was too high in previous lower resolution calculations, partly due to two-body effects 9. Thus they showed that it was possible for galaxies to exhibit stellar spiral arms in the absence of gas. Indeed such galaxies, with spiral arms but no recent star formation or large gas reservoir, are now observed (Masters et al., 2010).
3.3. Physical processes in the ISM
The gas in galaxies is subject to many processes other than spiral shocks, including cloud-cloud collisions, hydrodynamic instabilities (see also Section 3.5.2) and stellar feedback, as well as gas self gravity, thermodynamics and magnetic fields. Even in a purely smooth stellar disc, these processes still lead to a considerable degree of substructure in the gas, if not long spiral arms (e.g. Shetty & Ostriker (2006), Tasker & Tan (2009), Dobbs et al. (2011)). In the presence of spiral arms, these processes will still clearly occur, often preferentially in, or modified by the spiral arms.
The quasi-periodic spacing of gas structures along spiral arms observed in some galaxies has long been supposed associated with a gravitational origin of Giant Molecular Clouds (GMCs) or Associations (GMAs) (Shu et al., 1972, Woodward, 1976, Elmegreen, 1979, Cowie, 1981, Elmegreen & Elmegreen, 1983b, Balbus & Cowie, 1985, Kim et al., 2002, Shetty & Ostriker, 2006). The dispersion relation for a gas disc, Equation 4 is often used to derive expressions for the expected mass and spacing of GMCs along a spiral arm. If we consider the gas which collapses on the shortest timescale, this occurs when dω / dk = 0, at a wavenumber k = π G Σg0 / cs2. The corresponding wavelength is then
 |
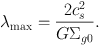(36) |
This is the predicted separation of the clouds. The mass of the clouds is then
 |
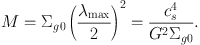(37) |
The spiral arms provide a denser environment, which can make the gas susceptible to instabilities at wavelengths where it would not be unstable in the absence of spiral arms. Also, as Σg0 increases, and cs likely decreases in the spiral arms, the properties of the GMCs change (though technically Equation 6, should be applied over large scales rather than localised to a spiral arm).
Whilst the dispersion relation adopts a number of caveats, e.g. a thin disc, these masses and spacings have been shown to approximately agree with simple numerical simulations of a gravitationally unstable isothermal medium (Kim et al., 2002, Shetty & Ostriker, 2006, Dobbs, 2008). These calculations ignored the multiphase nature of the ISM (though see Elmegreen (1989)), which with the inclusion of thermal instability and turbulence, may lead the thermal term to actually promote rather than prevent instability (Elmegreen, 2011). In a medium of clouds and diffuse gas, self gravity can also act to increase cloud collisions (Kwan & Valdes, 1987) which would not necessarily lead to the same masses and separations as Equations 36 and 37. Finally these estimates of the mass and separation generally require that the maximum cloud mass is reached before feedback disrupts the cloud, or the cloud moves out of the spiral arms (see also Elmegreen (1994), Elmegreen (1995)).
Cloud collisions occur regardless of spiral arms due to the random dispersion of the clouds, but are much more frequent in the spiral arms. As will be discussed in Section 3.5.2, dissipative collisions of either smaller molecular clouds or cold HI can lead to the formation of more massive GMCs. Structure is always present in the ISM, so gas entering the spiral arms will exhibit some structure (though the gas need not be molecular). Even for a homogenous warm medium, rapid cooling in the spiral shock quickly leads to thermal instabilities and the formation of structure (Dobbs et al., 2008, Bonnell et al., 2013). Like gravitational instabilities, cloud collisions in the spiral arm induce a spacing between GMCs. In this case, the spacing predominantly depends on the strength of the shock the gas encounters, which in turn depends on the spiral forcing or amplitude and the sound speed. The separation of GMCs is proportional to the epicyclic radius, which represents the radii of the disc over which material can be brought together to a single point, or into a single cloud (Dobbs, 2008). Stronger shocks produce more massive, widely spaced clouds. In this sense the behaviour is opposite to gravitational instabilities.
Parker instabilities have also been proposed to form GMCs in spiral arms (Mouschovias et al., 1974, Mouschovias et al., 2009, Elmegreen, 1982) and shown to produce density enhancements of factors of several, which may be sufficient to induce a phase change in the ISM. Density enhancements solely due to Parker instabilities are finite, and thus likely to be overwhelmed by gravitational instabilities (Elmegreen, 1982, Kim et al., 2001, Santillán et al., 2000, Kim et al., 2002). However there is some evidence of loops caused by Parker instabilities in the Galactic Centre, where magnetic fields are strong (Fukui et al., 2006).
All these processes lead to considerable substructure in the gas on size scales up to the most massive GMCs. Either fragmentation (via gravitational instabilities) or agglomeration of clouds leads to a mass spectrum from masses of < 100 M⊙ up to giant molecular associations of 107-8 M⊙. In the case that Ωp < Ω (i.e., R < RCR), complexes formed by all these methods leave the arms and are sheared out into trailing spurs (see next section) by differential rotation.
As well as processes which lead to the accumulation of gas into clouds, stellar feedback also has a substantial effect on the gas. Although spiral shocks may account for the very narrow dust lanes in galaxies, the width of the shocked region, both from Shu et al. (1972) and simulations (e.g. Wada & Koda (2004), Dobbs & Bonnell (2006), Shetty & Ostriker (2006)) is very narrow compared to the width of CO arms in nearby galaxies. Comparing with the Canadian Galactic Plane Survey (CGPS)), Douglas et al. (2010) found that HI velocity longitude maps from simulations without feedback produced too narrow spiral arms compared to the Milky Way. Stellar feedback also produces bubbles and holes in the ISM. Dobbs et al. (2011), and also Shetty & Ostriker (2008), showed that with large amounts of feedback, it is possible to largely erase the pattern of the original imposed stellar spiral potential. Thus the substructure associated with that of the stellar feedback becomes comparable to the imposed spiral pattern (similar to the stochastic star formation scenario, Section 2.5).
3.4. Substructure along spiral arms
Substructure reflects both giant molecular clouds, as well as branches, spurs and feathers which extend at clear angles away from the (typically) trailing side of the arm (see Figure 16). Branches, spurs and feathers are observed in many spiral galaxies, and occur in numerical simulations. As we will see, the formation of these features is different for the different spiral arm models.
 |
Figure 16. A section along the southern spiral arm of M51, from the Hubble Heritage image. Gas flow is predominantly left to right in the figure. The spiral arm spans the figure, with 2 massive complexes along the dust lanes of the spiral arms, containing HII regions, suggesting that star formation occurs very quickly once clouds form. Below the spiral arm, are narrow lanes of gas and dust, also connected with HII regions. We term these features spurs in this paper. Some spurs extend to the next spiral arm. Bridges, which would be more associated with a bifurcation in the arms, are not particularly evident in M51. The figure is taken from Elmegreen (2007) and is originally form a Hubble Heritage image, and is reproduced with permission from AAS ©. |
There are no formal definitions of branches, spurs and feathers. Spurs and feathers in particular have multiple meanings in the literature. Branches generally describe long structures which may go from one arm to another, and/or where one arm bifurcates into two. Consequently it may not be clear in an observed galaxy whether a feature is actually a branch or a spiral arm (including the Local Arm, Carraro (2013)). Spurs and feathers tend to be shorter features, and often describe quasi-periodic rather than isolated features. In their observational study, La Vigne et al. (2006) used feathers to refer to dust lanes which extend between spiral arms, and spurs to describe strings of star formation in the inter arm regions. However these 'feathers' typically harbour the regions of star formation or young stars, so theoretically there is no clear need to distinguish between these two types of feature. Chakrabarti et al. (2003) use an alternative notation, whereby spurs are leading features and feathers trailing. Although they found both in numerical simulations, it is not clear observationally whether such leading features are seen in actual spiral galaxies. Finally Dobbs & Bonnell (2006) referred to spurs as any relatively short (i.e. less than one inter arm passage), narrow trailing features seen in the gas, the definition we adopt here.
3.5. Quasi-stationary density waves
The response of gas to spiral arms has been considered most in the context of quasi-stationary spiral density waves, where, in the case of a simple sinusoidal stellar potential, an analytic solution for the response of the gas can be obtained. Motivated by the suggestion that narrow dust features seen in external galaxies might be due to shocks, Fujimoto (1968) first examined the response of gas to a spiral potential. He confirmed that the gas would indeed be likely to undergo a shock. Roberts (1969) extended this analysis and, with a small correction to the work of Fujimoto (1968), obtained four equations which can be solved to obtain the velocities, spatial coordinates and density of a parcel of gas as it moves round the disc (i.e. along a streamline). These equations demonstrate that the properties of the shock, and indeed whether there is a shock, depend on the amplitude of the spiral potential (F), the sound speed and/or the turbulent velocity of the gas, σg, the pitch angle and location in the disc. For example, for warm gas and moderate forcing, a narrow shock is expected ahead of the minimum of the potential (Figure 17). If the gas is cold however, a very narrow shock is expected after the minimum of the potential. Magnetic fields are not found to greatly affect the solution, the shock is merely weaker in the magnetic case (Roberts & Yuan, 1970).
 |
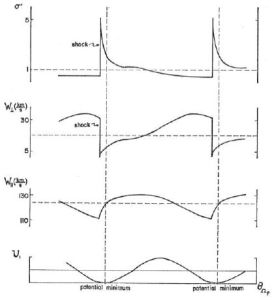Figure 17. Illustration of a typical shock solution for the gas response to a steady spiral density wave, from Roberts (1969). Gas flows from left to right. The figure shows density (top), velocity perpendicular to the spiral arms (second), velocity parallel to the spiral arms (third), and the potential (last), versus the azimuthal angle around the galaxy. Figure reproduced with permission from AAS ©. |
Another interpretation of spiral shocks was put forward by Kalnajs, and shown in Toomre (1977). Here the spiral forcing is considered analogous to a series of pendulums. The pendulums are assumed to oscillate like harmonic oscillators and bunch up periodically at certain intervals. The bunching up of the pendulums is analogous to parcels or clouds of gas crowding together at the spiral arms. Toomre (1977) supposed that gas clouds pile up at the locations of the spiral arms, a little like a traffic jam. A simple calculation of test particles in a spiral potential obeys this behaviour. In the case of spiral density waves with gas pressure, Shu et al. (1973) found that for cs = 8 km s-1, the forcing required to produce a shock is around a few %.
Shu et al. (1972) also investigated the dynamics of spiral shocks in the context of cloud collisions. They assumed a steady state solution and solved the jump conditions at the shock, in order to study the resultant shock structure for a two phase medium, consisting of cold clouds of a given filling fraction surrounded by warm intercloud medium. The different phases exhibit different density enhancements (of around 10 and 40), as expected, and they were able estimate a width of the shocked region of 50 pc, essentially the length scale after which the medium re-asserts an equilibrium state. Processes such as cloud collisions, and supposed gravitational fragmentation, led the authors to suppose a dynamic, rather than quasi-stationary shock scenario. Furthermore clouds will have dispersions relative to each other, and enter the spiral arms at different locations, and velocities.
Since the 1960s and 1970s, there have been many studies that have underlined the complex response of gas to spiral density waves, and departures from the Roberts (1969) picture. The gas structure along the arms arises through i) resonances, ii) instability of the spiral shock, and, iii) additional physical processes such as self gravity, cloud collisions etc. which were discussed in Section 3.3. Resonances are intrinsic to the underlying stellar potential, although they can be enhanced by self gravity in the gas. Processes included in ii) and iii) depend on the properties of the gas. But essentially all induce the formation of secondary, or substructure within the gaseous spiral arms.
Resonances are one means to generate gaseous substructure along spiral arms, specifically for the case of quasi-stationary density waves. Resonances occur when the epicyclic frequency, κ of the stellar orbits are some integer multiple of the angular frequency in the rotating frame of the spiral potential, or vice versa, thus
 |
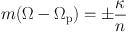(38) |
where Ωp is the pattern speed of the spiral, and m is the number of spiral arms in the stellar disc. In this case stars perform n radial oscillations every encounter with the m-armed spiral pattern. Determining the presence and location of resonances in the disc implicitly assumes that the pattern speed, Ωp, does not vary with radius or time. In the vicinity of resonances, the behaviour of stellar and or gas orbits are abruptly altered and become nonlinear (e.g. Contopoulos & Grosbol (1986), Contopoulos & Grosbol (1988)). The primary resonances at the ILR and OLR (n = 1) are, as discussed in Section 2.1.2, associated with the boundary of where the spiral density waves exist. Thus we are predominantly interested in resonances within these radii. Shu et al. (1973) supposed that the gas would be expected to experience perturbations due to resonances, and showed analytically that gas undergoes a secondary compression to a spiral potential at the ultraharmonic resonance (n = 2) 10. Woodward (1975) demonstrated the nonlinear response of gas at the location of the ultraharmonic resonance with 1D calculations, and there have since been many further 2D and 3D (Smoothed Particle Hydrodynamics (SPH) and grid code) calculations (Bertin, 1993, Patsis et al., 1994, Patsis et al., 1997, Chakrabarti et al., 2003). In particular Patsis et al. (1994) showed the bifurcation of the spiral arms at the 4:1 resonance (as also predicted by Artymowicz & Lubow (1992)), provided there is a spiral forcing of F 5 %.
Chakrabarti et al. (2003) showed the development of more varied features, including branches (bifurcations) and shorter leading and trailing features (spurs / feathers), again occurring primarily near the 4:1 resonance, with the morphology of the feature dependent primarily on the level of forcing of the spiral potential. Chakrabarti et al. (2003) suppose that flocculence in spiral galaxies could be due largely to such resonant features, an idea recently followed up by Lee & Shu (2012), where they investigate the possibility that higher order resonances lead to the formation of multiple spurs along the arms. There is a notable difference between the work of Lee & Shu (2012), and GMC formation by gravitational instabilities in the gas or cloud-cloud collisions (which are subsequently sheared into spurs). For the former, the location of the spurs does not change over time, the GMCs always forming and dispersing in the same place in the spiral arms (seemingly less likely in a dynamic environment). For other GMC formation mechanisms there is no expectation that clouds form in the same place.
3.5.2. Stability and structure of the shock
Even in the non-magnetic, non self gravitating regime, several authors have questioned the stability of spiral shocks. From analytical work, Mishurov & Suchkov (1975) first proposed that the flow through a spiral shock could be unstable. In contrast Nelson & Matsuda (1977) solved the fluid equations numerically in 1D, and predicted that the flow should be stable (see also Dwarkadas & Balbus (1996)) although their solutions indicate some asymmetric features. Wada & Koda (2004) pointed out that the latter studies adopted a tightly wound pattern, and a flat rotation curve. They performed 2D numerical simulations with different pitch angles and rotation curves, and found the spiral arms to be Kelvin-Helmholz unstable when a more open spiral pattern was used. The instability is most readily seen as spurs along the spiral arms. Kim & Ostriker (2006) found that in 3D numerical models, Kelvin-Helmholtz instabilities were suppressed, although Kim et al. (2014) suggest an alternative 'wiggle instability' mechanism.
Dobbs & Bonnell (2006) (see also Dobbs (2008)) supposed a different mechanism for producing structure, and spurs in particular, along the shock in the purely hydrodynamical, non self-gravitating case. They supposed that any substructure in the gas gets amplified as it passes through a shock. Thus, like the cloud collisions in the Toomre (1977) model, clouds, or structure in the gas, get forced together by orbit crowding in the spiral shock. A similar idea was shown in Roberts & Stewart (1987). Although they do not perform hydrodynamic calculations, clouds in their models undergo dissipative collisions. Like Toomre (1977), clouds can be forced together and move apart after the shock, but unlike Toomre the presence of dissipation means some clouds are effectively compressed together and retain structure after the shock. Dobbs & Bonnell (2006) showed that this process was only valid in the presence of cold gas, when the ISM is subject to thermal instabilities (Dobbs et al., 2008) unless there is very large spiral forcing. For a warm medium, the spiral shock is relatively weaker and the pressure smoothes out any structure in the gas. The same process could have also plausibly operated (rather than Kelvin Helmholtz instabilities) in the calculations by Wada & Koda (2004) and Kim & Ostriker (2006).
In the presence of self gravity, Lubow et al. (1986) showed using 2D calculations that the gas experiences a reduced shock from the stellar potential. In an extreme case, where all the gas is situated in self gravitating clouds, the behaviour of the clouds would resemble the zero pressure case, similar to billiard balls entering the potential. Wada (2008) performed full 3D hydrodynamical simulations with self gravity and a multi-phase medium, finding that the intermittency of dense gas entering the spiral potential leads to a non steady state, where the gas spiral arms are neither continuous, nor exhibit a constant offset from the arms (see Figure 18, and e.g. also Dobbs & Pringle (2013)). Rather the arms switch back and forth with time. Consequently Wada (2008) does not call the response of the gas a shock in this context. The behaviour of the gas is quite different from the original Roberts (1969) picture largely because the gas is far removed from a homogenous flow. Also, simulations with a multiphase medium typically do not exhibit a shock or peak in density before the spiral potential. Typically the gas density peaks after, or coincident with the minimum of the potential, because the cold gas (within a multi-phase medium) shocks later.
Figures 16 and 18 illustrate a number of the points made in Section 3.5, for a section of spiral arm in M51 and a numerical simulation respectively. The various processes in the ISM, including instabilities, turbulence and feedback lead to a 'shock', or dust lanes that are very much more structured and broad than the simple analytic case. Nevertheless the response of the gas is still much sharper than the underlying potential or old stellar population. With gravity and cooling, trailing spurs are very easy to make from arm GMCs. As discussed in the next section, we would expected these features regardless of whether the arms are tidally induced and slowly winding up or truly stationary, the only difference for the dynamic arms being the absence of trailing spurs.
 |
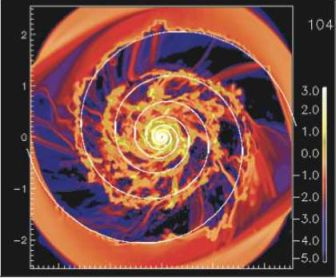Figure 18. The response of gas to an m = 2 fixed spiral potential is shown, from Wada (2008). The minima of the spiral potential are indicated by the white lines. The simulation include a multiphase medium, and stellar feedback, so the response of the gas is highly complex. No clear continuous shock is found, and the density peak of the gas does not have a continuous offset from the minimum, although typically the density peak is after (on the trailing side of) the potential minimum. |
3.6. Tidally induced spiral arms
As discussed in section 2.4, the main difference for tidally induced spirals compared to the QSSS case is likely to be a radially dependent (Oh et al., 2008, Dobbs et al., 2010), rather than constant pattern speed 11. Consequently resonance related substructure is not likely to feature in tidally induced spirals.
At large radii, the spiral arms may well be material arms, with little gas flow through the arms (Meidt et al., 2013). However at most radii, as mentioned in section 2.4, the arms are likely to be density waves, with a pattern speed lower than that of the rotation speed (unlike the local, transient arms). Similar to the quasi-stationary density wave picture, the gas will flow through the arms and experience a spiral shock. GMCs are expected to form in the arms by the means described in Sections 3.3 and 3.5, being sheared out into spurs as they leave the arms. The structure of galaxies such as M51 largely reflects this behaviour.
The simulations of Salo & Laurikainen (2000b) and Dobbs et al. (2010) did not achieve the resolution required to study GMC formation, or spur formation, in their models of interacting galaxies . The simulations do predict that unlike the quasi-steady state spiral galaxy, the gas and stars are not found to be offset from each other. In their model of M51, Dobbs et al. (2010) also showed that the double, and relatively close passage of the perturbing galaxy introduced somewhat chaotic dynamics, inducing large radial inflow and outflow motions (see also Shetty et al. (2007)). The chaotic dynamics also mean that the spiral arms may move with respect to the gas on relatively short (∼ 10 Myr) timescales.
3.7. Gas flow in dynamic spiral arms
The main difference in the behaviour of gas in galaxies with dynamic spiral arms, compared to quasi-stationary or tidally induced arms, is again due to the pattern speed. Dynamic stellar spiral arms do not exhibit significantly different rotation from the rest of the galaxy. Rather the spiral arms exhibit corotation everywhere (e.g., Baba et al., 2013, see Section 2.2.2). Thus the gas, stars and spiral arms will have the same angular velocities and there is no gas flow through the arms. Similar to the case of tidally induced spiral arms, the dynamics of the spiral arms means substructure due to resonances cannot occur.
In dynamic arms, the gas is still subject to the gravitational potential of the arms. As shown in Dobbs & Bonnell (2008) and Wada et al. (2011), gas effectively falls in to the minimum of the potential, from both sides of the spiral arm. In massive gas rich discs, the spiral arms may themselves be a manifestation of gravitational instabilities in the gas, so gas infall is coincident with arm formation. For dynamic arms, a systematic offset is not expected between the density peak of the gas, and the stellar minimum (Dobbs & Bonnell, 2008, Wada et al., 2011). Because the gas does not flow through the spiral arm, the gaseous arm remains until the stellar arm disperses. Even then, since the velocity dispersion in the gas will be less than that of the arms, it will still be likely that a gaseous arm remains, even when the stellar arm has dispersed (Dobbs & Bonnell, 2008)
Gas can still clearly undergo shocks as it falls into the minimum of the potential, particularly if it has cooled. Shocks in nearby spiral arms were associated with the dynamic spiral arm picture, as well as the QSSS scenario in early observations (e.g. Quirk & Crutcher (1973)). The presence of quasi-regular spurs however seems less likely in galaxies with dynamic spiral arms. As stated in Section 3.5.2, spurs are usually the result of GMCs in spiral arms being sheared out as they move into the inter arm regions. However if the gas does not pass out of the spiral arms, this mechanism is not feasible, and indeed spurs are not typically seen in simulations (Dobbs & Bonnell, 2008, Wada et al., 2011). Larger features, such as branches, are possible though. As mentioned above, when the stellar spiral arm dissolves, the gaseous arm may remain intact for longer. The gaseous arm thus represents a feature without a stellar counterpart, can appear as a branch between spiral arms (Dobbs & Bonnell, 2008).
Again, GMC formation will occur as described in Section 3.3. So far, there is no noticeable difference between the properties of GMCs in simulations of galaxies with global spiral spiral arm versus local transient arms (Hopkins et al., 2011, Dobbs et al., 2011), and likely not different to tidal arms. However there are differences in comparison to the clouds in a completely smooth stellar disc, where there are no stellar spiral arms, and processes such as cloud-cloud collisions are more limited. In the case without spiral arms, the maximum cloud mass is smaller (e.g. a few 105 M⊙ compared to a few 106 M⊙), whilst clouds tend to preferentially exhibit prograde rotation rather than randomly orientated rotation.
9 Note that Sellwood (2012) disagrees two body effects are important, rather he supposes the main difference with higher resolution is that there is lower amplitude noise, which results in weaker spiral arms and less heating. Back.
10 For m = 2 spirals, the ultraharmonic resonance is called the 4:1 resonance. Back.
11 although there are some exceptions to this view, Salo & Laurikainen (2000b) find a constant pattern speed in the centre of their models of M51, whilst Meidt et al. (2008b) adopt a model of multiple patterns for M51. Back.