2. GENERATION OF SPIRAL STRUCTURE

In this section we describe the different mechanisms for generating spiral structure, namely quasi-stationary density wave theory (Section 2.1), recurrent transient spiral instabilities (Section 2.2), bars (Section 2.3), tidal interactions (Section 2.4), stochastic star formation (Section 2.5), and exotic mechanisms such as perturbations from dark matter halos (Section 2.6).

2.1. Quasi-stationary density wave theory

In this section we present the theory that global spiral arms are slowly evolving patterns that rotate with fixed pattern speeds in the disc, quasi-stationary density wave theory. Much of this material is theoretical, as we discuss in Section 2.1.5, this theory has not yet been demonstrated in the context of numerical simulations.

Inspired by the idea of kinematic density waves suggested by Lindblad (1960), Lindblad (1963), Lin & Shu (1964) proposed a self-consistent density wave theory. Unlike Lindblad's approach Toomre (1977), Pasha (2004a), Pasha (2004b, for reviews), Lin & Shu treated the galactic disc as a 'continuum' consisting of either stars or gas, and derived the dispersion relation of the density waves for a rotating disc. Qualitatively, they assumed that the spiral arms are not material in nature, but instead made up of areas of greater density, with the stars and gas moving through the spiral arms. The difference in the dynamics is often compared to cars moving along a traffic jam. Material arms are analogous to a queue of cars moving at a speed v₀ identical to all other vehicles on the road. For density waves, instead suppose a queue of cars moving at v₁ < v₀, whereas other cars on the road will slow down to v₁ as they enter the queue and speed up as they leave.

After the derivation of the dispersion relation for a fluid disc by Lin & Shu (1964), the dispersion relation for a stellar disc was derived by Lin & Shu (1966) and Kalnajs (1965). The dispersion relations for fluid and stellar discs are called the Lin-Shu dispersion relation and Lin-Shu-Kalnajs dispersion relation, respectively. We first outline the physical meaning of the dispersion relations based on the linear tight-winding density wave theory of fluid and stellar discs (Section 2.1.1). Then, we explain the global mode theory of galactic discs (Section 2.1.4). The behaviour of gas in quasi-stationary density waves will be described in Section 3.5.

.2.1.1. Dispersion relations of tight-winding density waves

Lin and Shu derived dispersion relations of fluid and stellar discs under the following approximations and assumptions:

1. Linear perturbations: They linearized the equation of continuity, the equations of motion (Euler equation), the equation of state, and Poisson equation, and then studied the behaviour of the linear perturbations. In this case, it is assumed that the unperturbed disc is axisymmetric and has no radial motions.
2. Tight-winding approximation (short wavelength or WKB ¹ approximation): Deriving the dispersion relation for a general spiral wave is extremely complicated because of the long-range force nature of gravity (see Section 2.1.4). They assumed the spiral arm has a small pitch angle in order that distant density perturbations can be neglected. In other words, the response of the matter to the gravity perturbations becomes local. In this approximation, the dispersion relation of density waves can be written down in terms of local quantities. If we write the radial dependence of any perturbation quantity (Equation 1) in terms of an amplitude and phase as

   (2)

   the tight-winding approximation corresponds to the assumption that the phase f(R) varies rapidly in comparison with amplitude (R), i.e.,

   (3)

3. Quasi-stationary spiral structure hypothesis (QSSS hypothesis): They hypothesized that 'global' spiral arms hardly change their shape during many galaxy rotational periods ('quasi-stationarity') based on empirical grounds (Lin & Shu, 1964, Bertin & Lin, 1996, Bertin, 2000). This is equivalent to assuming that the rotation of global spiral arms is rigid-body rotation with a specific angular velocity and pitch angle. This fixed angular speed is called the pattern speed. In the inner parts of galaxies, stars and gas rotate faster than the pattern speed, and overtake the spiral arm. In the outer parts of galaxies, stars and gas rotate slower than the pattern speed, and the spiral arms overtake the stars and gas.

Taking into account these approximations and assumptions, the Lin-Shu theory is often called a linear tight-winding, or quasi-stationary density-wave theory.

Since the stars occupy most of the mass of the galactic disc, the dispersion relation of the density wave of a stellar disc is important in understanding the spiral arms. However, the dispersion relation for a fluid disc is simpler, so we introduce this first, before discussing the dispersion relation for a stellar disc. We refer the reader to Binney & Tremaine (2008) and Shu (1992) for the mathematical details on derivation of dispersion relations, as well as Bertin & Lin (1996) and Bertin (2000) for further discussion on the concept of quasi-stationary density wave theory.

The dispersion relation for linear tight-winding perturbations in the razor-thin fluid disc (Lin-Shu dispersion relation; LS dispersion relation) is given by

(4)

(Lin & Shu, 1964). Here Ω, Σ₀, c_s and κ are the angular frequency, surface density, sound speed and epicyclic frequency

(5)

of the fluid disc, respectively. These quantities depend on the galacto-centric radius R and define the axisymmetric basis state. ω, k, and m are the angular frequency, radial wave-number, and the number of spiral arms, respectively. The radial wave-number k is related to the phase of the radial dependence of the perturbations f(R) (Equation 2) via

(6)

We define k > 0 for a trailing spiral arm and k < 0 for a leading spiral arm. Note that the so-called pattern speed Ω_p is defined as ω / m.

In the inertial frame, ω on the left hand side of Equation (4) is the angular frequency of the density wave. In the rotating frame at some radius R in the disc, (ω - mΩ) is the angular frequency of the density wave experienced by a star at R. A perturbation to the disc will be of the form exp[-i(ω - mΩ)t]. Positive (ω - mΩ)² means that the perturbations to the disc will be stable. However negative (ω - mΩ)² means that the perturbations will be of the form exp[±|ω - mΩ|t] and there is a perturbation whose amplitude grows exponentially, thus the disc is unstable. Therefore, the right-hand side of equation (4) indicates the stability of the density waves. Here, we can introduce a dimensionless parameter

(7)

known as the Toomre Q parameter, such that if Q > 1, (ω - mΩ)² > 0 for all radial wave-numbers k, while if Q < 1, (ω - mΩ)² becomes negative for a range of radial wave-numbers. Therefore Q gives us a criterion whether the disc is unstable or not to tight-winding perturbations ² We can also define a critical unstable wavelength λ_crit = 2 π / k_crit, where (ω - mΩ)² = 0 for a cold fluid disc (i.e., c_s = 0). In this case, all perturbations with wavenumber |k| < k_crit or wavelength λ > λ_crit are unstable, where k_crit = κ² / (2π G Σ₀) or λ_crit = 4π² G Σ₀ / κ². Note k_crit = k_min / 2, where k_min is defined such that (ω(k_min) - mΩ)² = 0 for a neutrally stable fluid disc (Q = 1).

Figure 2a shows the Lin-Shu dispersion relations for different Q values. Figure 2a shows that high Q values (stability) occur for density waves with large wavelengths and angular frequencies. The physical meaning of each term of the right-hand side of equation (4) is as follows. The first term, c_s² k², expresses the effect of pressure, which being positive stabilizes the fluid against perturbations. This is the same as the dispersion relation of sound waves. The second term, κ² represents rotation, which again stabilizes the disc. The third term, which incorporates the self gravity of the disc, promotes the growth of instabilities. When the effect of self-gravity exceeds the limit where (ω - mΩ)² is non-negative, a real root does not exist and it is impossible for a stable density wave to exist. Thus, the LS dispersion relation shows that the (gaseous) spiral density wave can be considered to be a sort of acoustic wave taking into account the effects of rotation and self-gravity.

Figure 2. Dispersion relations for tight-winding density waves in a fluid disc (left) and stellar disc (right). Waves of a wavenumber smaller than that at the minimum frequency (|k| ≪ kcrit) are called long waves, while those with |k| ≫ kcrit are called short waves. The critical wavenumber kcrit is defined as κ2 / (2π G Σ0).

Consider now a stellar disc. The dispersion relation for linear tight-winding perturbations a in razor-thin stellar disc with a modified Schwarzschild distribution (Lin-Shu-Kalnajs dispersion relation; LSK dispersion relation) is given by

(8) (9)

(Lin & Shu, 1966, Kalnajs, 1965). Here, σ_R is the radial velocity dispersion of the stellar disc, and I_n is a modified Bessel function. Figure 2b shows the LSK dispersion relations for different Q values defined by

(10)

The behaviour of the dispersion relation is similar to the LS relation for smaller radial wave-number (larger wavelength), but in the the larger radial wave-number (shorter wavelength) regime, the behaviour of the two is decidedly different. For the short-wave regime, the LSK dispersion relation approaches (ω - mΩ)² / κ² = 1 asymptotically, but the LS dispersion relation extends to (ω - mΩ)² / κ² > 1. This difference originates in the essential difference between the pressure for a fluid disc, and the velocity dispersion for a stellar disc: In the case of fluid discs, pressure will become large at small wavelengths. In contrast, since the stellar disc is collisionless, there is no such repelling force. Instead the frequencies of perturbations cannot become larger than the epicyclic frequency κ.

2.1.2. Propagation of tight-winding density waves

Although we have discussed waves as being quasi-stationary in the previous section, in reality if a wave is induced in the disc, it will propagate radially with some group velocity, rather than being stationary. In this and the next sections, we will discuss the group velocity and describe the further developments in density wave theory (the setting up of suitable boundary conditions) which allow the possibility, at least theoretically, of setting up a standing wave. The propagation of the tight-winding density waves is reviewed throughly in Grosbøl (1994) and Binney & Tremaine (2008).

The original density wave theory (Lin & Shu, 1964) is based on the QSSS hypothesis which assumes that the amplitude and shape of the spiral arm are independent of time. However, since the angular frequency ω depends on radial wave-number k via the LS or LSK dispersion relations (eqs. 4 and 8), the energy and angular momentum of the density waves propagate radially as wave packets (Toomre, 1969). This propagation velocity is the group velocity, given by v_g = ∂ ω(k,R) / ∂ k. If we consider propagation of density waves in a fluid disc, following the LS dispersion relation (Equation 4), the group velocity of a wave packet is

(11)

where positive and negative signs indicate trailing (k > 0) and leading (k < 0) spiral waves, respectively.

The sign of the numerator of this equation is negative for short waves and positive for long waves, and the sign of the denominator is negative and positive for R < R_CR and R > R_CR, respectively. Thus, short trailing and long leading spiral waves will propagate away from the coronation (CR) radius, while the short leading and long trailing spiral waves will approach the CR radius (propagation directions are indicated by arrows in Figure 3). Note that if the disc has a large Q, a forbidden region emerges in the vicinity of the CR, where due to the pressure or random motions the density waves diminish.

The behavior is essentially same for stellar density waves except for regions around the inner and outer Lindblad resonances (ILR and OLR). The difference around the ILR/OLR originates in the difference in dynamical behavior between stars and fluid (Section 2.1.1). The propagation digram for stellar density waves following the LSK dispersion relation (Equation 8) is shown in Figure 3. Long stellar density waves (|k / k_crit| ≪ 1) are reflected at the Lindblad resonances (Goldreich & Tremaine, 1978, Goldreich & Tremaine, 1979) while short waves (|k / k_crit| ≫ 1) are absorbed there due to Landau damping (Lynden-Bell & Kalnajs, 1972). Thus, both long and short stellar density waves cannot pass through the Lindblad resonances. Therefore, the permitted region for stellar density waves is restricted between the ILR and OLR radii (with the exception again of the forbidden region). However, this does not necessarily imply that stationary density waves will exist here.

Figure 3. Propagation diagram for tight-winding stellar density waves following the LSK dispersion relation (Equation 8). The disc is assumed to have a flat rotation curve and constant Toomre's Q = 1.2. The horizontal dashed lines are the OLR radius (upper), CR radius (middle), and ILR radius (lower), respectively. The arrows indicate the directions of group velocities. Long waves (|k / kcrit| ≪ 1 ) are reflected at the Lindblad resonances, while short waves (|k / kcrit| ≫ 1 ) are absorbed there due to Landau damping.

If we apply the group velocity formula to the solar neighborhood, v_g ∼ 12 km s^-1 the stellar density wave takes ∼ 400 Myr to propagate 5 kpc radially. This timescale is comparable to the rotation period of the Galaxy. Therefore, the stellar density waves will have a short lifetime of order < 1 Gyr (Toomre, 1969).

This problem can be solved if the density waves are reflected in the central region before reaching the ILR, and amplified by some mechanism. An absorption of the short stellar density waves at the ILR can be avoided if the Toomre's Q parameter increases significantly (forming a so-called Q-barrier) refracting the density wave outside the ILR. Short trailing stellar density waves can be excited near the CR from long trailing stellar density waves by 'the wave amplification by stimulated emission of radiation' (WASER) in lighter discs (Mark, 1974, Mark, 1976), or from short leading density waves by the swing amplification mechanism in heavier discs (Goldreich & Lynden-Bell, 1965b, Julian & Toomre, 1966, Goldreich & Tremaine, 1978, Toomre, 1981). With these assumptions, 'standing-wave' patterns ³ can exist between a reflecting radius in the inner part of the galaxy and CR radius, where the waves can be amplified (Bertin et al., 1989a, Bertin et al., 1989b). The spiral density waves should be located between, but not reaching the ILR and OLR.

2.1.3. Swing amplification

The quasi-stationarity of spiral arms requires wave amplification mechanisms such as WASER (Mark, 1974, Mark, 1976) or swing amplification (Goldreich & Lynden-Bell, 1965b, Julian & Toomre, 1966, Goldreich & Tremaine, 1978, Toomre, 1981). In the WASER (swing amplification) mechanism, a trailing (leading) wave is turned into a trailing wave when crossing CR and is greatly amplified in the process. It is noted that there is no conflict between the swing amplification and WASER (Lin & Thurstans, 1984, Bertin et al., 1984, Bertin et al., 1989b). The reason they have been considered differently is largely historical, reflecting opposing views at the time. However, if discs have non-negligible self-gravity at CR, the swing amplification mechanism can greatly dominate amplification by the WASER mechanism. On the other hand, in a system where the disc mass is only a small fraction that supports the rotation curve, the WASER mechanism can underline the growth of the most important spiral mode, as long as Q ≃ 1 at CR (Shu, 1992, Bertin & Lin, 1996, Bertin, 2000).

We focus on the swing amplification mechanism as a wave amplification mechanism for sustaining quasi-stationary density waves between the ILR and OLR. The so-called swing amplification works when short leading waves are reflected to short trailing waves at the CR radius, or when a density enhancement formed by self-gravity is stretched out by differential rotation. The dynamical response takes the form of wavelets in the surrounding medium, each amplified by its own self-gravity through the swinging of leading features into trailing ones due to shear.

The swing amplification operates through a combination of three ingredients: the shearing flow, epicyclic motions, and the disc self-gravity. Toomre (1981) interpreted the swing amplification mechanism in terms of the wave-particle interaction between spiral arms and stars. Since the direction of epicyclic motion of a star is the same as the direction which the spiral arm is sheared by differential rotation, stabilisation by rotation is reduced, and the perturbation can grow via the usual Jeans instability (Goldreich & Lynden-Bell, 1965b, Julian & Toomre, 1966, Goldreich & Tremaine, 1978). The timescale of epicyclic motion (κ^-1) is comparable to the timescale of involvement with the spiral arm (A^-1 where A is Oort's constant), and unless Q ≫ 1, the structure can grow in a short time comparable to κ^-1. The resulting spiral structure from this process is generally expected to be chaotic (Sellwood, 2011) rather than lead to a symmetric spiral pattern.

Consider a local region of a galactic disc away from the galaxy center. Since the galactic rotation is parallel to this local region (curvature can be ignored), we set an x and y-axis aligned with the radial and rotational directions of the galaxy respectively. In this case, the equations of motion of the stars are given by

(12) (13)

(using the Hill approximation). Here, x = R- R₀, y = R₀ (φ - Ω₀t), and Ω₀ and A₀ ≡ -1/2 R₀(dΩ / dR)₀ are the angular velocity and Oort's constant at R₀, respectively. f_⊥ indicates the gravitational force perpendicular to the spiral arm. γ is an angle between the spiral arm and radial direction of the galaxy: γ = 90^∘, γ < 0, and γ > 0 correspond to a ring, leading, and trailing structures, respectively.

Defining the normal displacement of the star perpendicular to the spiral arm,

(14)

as a new variable, the equations of motion reduce to an equation

(15)

where the squared spring rate is given by

(16) (17)

and

(18) (19)

Figure 4 shows dependence of the spring rate on galaxy parameters of (Γ, Q, X). In the case of Γ = 0 (i.e, the galaxy has rigid-body rotation), the spring rate is always positive. Thus, the stars cannot be trapped by the spiral arm, and then the spiral arm does not amplify. In other words, the swing amplification cannot work without differential rotation.

Figure 4. Squared spring rate S(γ) as a function of the angle γ between the spiral arm and radial direction of the galaxy for Γ = 0.0 (rigid rotation) and Γ = 1.0 (flat rotation). Different lines indicate Q = 1.0 (black), 1.2 (red), and 1.5 (green), respectively. Spring rates are calculated based on the equations of motion in Toomre (1981) and Athanassoula (1984). The squared spring rate is always positive in the case of Γ = 0.0, but it can be negative in the case of Γ = 1.0. Thus, the normal displacement of the stars around the spiral arm ξ can grow exponentially as the spiral arm is sheared by differential rotation.

By the transformation of variables to γ, instead of time t, Equation 17 becomes

(20)

Numerical integration of this differential equation gives the dependence of the swing amplification factor on the galaxy parameters (Γ, Q, X) shown in Figure 5. The effect of self-gravity and the winding of the spiral arm work in synergy, so that a star comes to stay at the spiral arm for a long time, and spiral arms are amplified temporarily. Note that the above argument is based on the linear analysis by Toomre (1981) and Athanassoula (1984). Fuchs (2001) solved linearised collisionless Boltzmann and Poisson equations self-consistently and showed that the result is essentially the same. Further, non-linear effects are studied in N-body simulations of local regions of stellar discs (Toomre, 1990, Toomre & Kalnajs, 1991, Fuchs et al., 2005), as well as N-body simulations of global stellar discs (Sellwood & Carlberg, 1984, Carlberg & Freedman, 1985, Bottema, 2003, Fujii et al., 2011, Baba et al., 2013, D'Onghia et al., 2013). D'Onghia et al. (2013) carefully demonstrated the growth of spiral arm features by swing-amplification and found a nonlinear evolution that is not fully consistent with the classic swing-amplification picture of Julian & Toomre (1966) and lasted longer than predicted by swing amplification (Toomre & Kalnajs, 1991) (see also Section 2.1.5).

Figure 5. The maximum amplification factor is shown as a function of the X, Γ and Q parameters. The amplification factor is calculated based on the equations of motion given in Toomre (1981) and Athanassoula (1984).

In order for the swing amplification mechanism to work continuously (Toomre & Kalnajs, 1991), we need to understand how leading waves are generated. One possibility is the case where there is no ILR. A trailing wave does not suffer from Landau damping at the ILR, instead the wave turns into a leading wave as it crosses the galaxy center. This is the so-called feedback loop proposed by Toomre (1981).

2.1.4. Global mode theory

Although linear density wave theory was successful in demonstrating the existence of a tight-winding spiral wave, the tight-winding density wave theory has room for improvement. Firstly, since they utilized the WKB approximation, this theory cannot be applied to very long waves (or open spiral arms) strictly. Secondly, the presence of neutral spiral density waves itself is theoretically questionable. It is critically problematic that a density wave propagates through a galactic disc radially in a few galactic rotations, and eventually disappears by absorption at the inner/outer Lindblad resonances (ILR/OLR). Thus, the 'quasi-stationarity' hypothesis is not ensured (Toomre, 1969, Section 2.1.2). Finally, the tight-winding theory cannot predict the number of spiral arms m and sign of the wave-number k (i.e., trailing or leading). In other words, the theory cannot explain why actual spiral galaxies prefer to have trailing two-armed spirals (k > 0 and m = 2) and what determines the angular frequency of the spiral density wave. In response to these criticisms, the tight-winding density wave theory developed into a global mode theory (e.g., Lau et al., 1976, Bertin et al., 1977, Aoki et al., 1979, Iye, 1978, Bertin, 1983, Bertin et al., 1984, Bertin et al., 1989a, Bertin et al., 1989b, Bertin & Lin, 1996).

A key nontrivial step at the basis of the derivation of the dispersion relation is the reduction of the long-range gravity law to a WKB dispersion relation between the perturbed potential and the perturbed density. Numerical integration of the basic perturbed equations is required. Since the first global mode analysis was applied to rotating fluid discs by Hunter (1965), there have been many studies, mainly in the 1970s-80s (e.g. Bardeen (1975), Aoki et al. (1979), Iye (1978), Takahara (1978)), as well as extending the analysis to rotating stellar discs (Kalnajs, 1972). In order to analyze the eigen-value problem of a stellar system, it is necessary to solve the density perturbations and the responsive orbital perturbations in satisfying the linearized collisionless Boltzmann equation and the Poisson equation, self-consistently. Although Kalnajs (1972) solved the eigenvalue problem of the Maclaurin disc using the so-called 'matrix method', numerical integration is required to solve the eigen-value problems of stellar discs (e.g. Athanassoula & Sellwood (1986), Sellwood & Athanassoula (1986), Sellwood (1989), Earn & Sellwood (1995), Vauterin & Dejonghe (1996), Pichon & Cannon (1997), Polyachenko (2004), Polyachenko (2005), Jalali & Hunter (2005)). However, these studies are somewhat limited due to the mathematical complexity.

Global mode analysis is based on a point of view that the spiral arms are manifestations of the gravitationally 'unstable' global eigen-oscillations of disc galaxies ⁴. This eigen-oscillation problem of the galactic disc resembles the problem of oscillating patterns of the skin when a drum is struck. Similar to the way oscillation patterns are controlled by how to stretch and how to strike the skin, oscillation of a galactic disc is controlled by the density and velocity-dispersion distributions of a galactic disc. However, there are two differences between eigen-oscillation problems of the drum and galactic disc. First, changes of the gravity from the oscillation should be taken into account to solve the eigen-oscillation problem of the galactic disc. This makes the problem very complicated. In the case of a drum, there is only a traverse wave, but for the oscillation of the galactic disc, there is also a longitudinal wave as well as a transverse wave. The transverse and longitudinal waves in the galactic disc are equivalent to the bending (warp) of a galactic disc and spiral arms, respectively.

Before explaining numerical results of the global mode analysis, let us consider the stability of fluid and stellar discs. Consider first the case of axisymmetric perturbations (Toomre, 1964, Goldreich & Lynden-Bell, 1965a). Qualitatively, we consider the case where an axisymmetric disc receives a perturbation illustrated by the small arrows shown in Figure 6(a). The fluid and stars in the disc move radially, and try to make a ring structure, but the pressure (or velocity dispersion), centrifugal, and Coriolis forces suppress growth of this ring perturbation. Left panel of Figure 7 shows the neutral stability curves for tight-winding spirals ((ω - mΩ)² = 0) showing Q-values as a function of λ / λ_crit. As Q for the disc is lowered, the disc moves from the stable to unstable regime. The wavelength which becomes unstable first is p λ_crit, where p = 0.5 in the case of a fluid disc and p = 0.55 in a stellar disc.

Figure 6. Axisymmetric perturbations (a) and bar-like perturbations (b) on an axisymmetric disc. The disc rotates anti-clock wise. Directions of the perturbations are indicated by small arrows.

Figure 7. Left: Neutral stability curves for tigiht-winding spiral instabilities based on the LS dispersion relation (red; Equation 4) and LSK dispersion relation (black; Equation 8). The region below the curve is stable against tight-winding spiral instabilities. Right: Neutral stability curves for open spiral instabilities based on the BLL dispersion relation (Equation 21) with = 0, 0.4, 0.6, 1.0, and 1.414.

In the case of spiral perturbations with a finite pitch angle (i.e., open spiral perturbations), the effects of the gravitational perturbation parallel to the spiral arm, and shear originating from differential rotation need to be taken into account. Again, we consider the case where an axisymmetric disc receives a perturbation given by the small arrows shown in Figure 6(b). In contrast to the case of Figure 6(a), the fluid and stars move in the azimuthal direction, and centrifugal and Coriolis forces do not appear. Thus, growth is not suppressed. The effect of the excessive centrifugal and Coriolis forces stabilises the perturbation with a long wavelength (Section 2.1.1 and Figure 2), it is expected that the stabilization effect will become weak in a long wavelength regime and that open spiral arms will become unstable.

This qualitative expectation is checked quantitatively below. Lau & Bertin (1978) derived the asymptotic dispersion relation of open spiral density waves in the fluid disc (Bertin-Lau-Lin dispersion relation; BLL dispersion relation):

(21)

where k = √k_R² + k_φ², k_R, and k_φ = m / R are the wave-number, radial wave-number, and azimuthal wave-number, respectively ⁵. We define two quantities

(22) (23)

where indicates a stability parameter which depends on the disc mass relative to the total mass and a shear rate of the disc, and є₀ is a parameter which relates to the degree of the self-gravity. In the LS dispersion relation, as described in Section 2.1.1, the disc is stabilized by the rotational (κ²) and pressure effects (k² c_s²) against self-gravity (2 π G Σ₀ k). In addition to these effects, the BLL dispersion relation includes within the rate of shear, dlnΩ / dlnR, as well as the self-gravity term, є₀.

Based on the BLL dispersion relation, a neutral stability curve for spiral instabilities is given by

(24)

where λ = 2π / k is a wavelength (right panel of Figure 7). If we set = 0, the neutral stability curve is equivalent to ones for the LS dispersion relation. From this neutral stability curve, a value of Q larger than unity is required for stability against spiral disturbances with a larger value of . This means that open spiral arms are difficult to stabilise and will, more often than not, result in growth.

Figure 8 shows the numerically integrated density contours of the global unstable modes with different 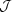and Q values (Bertin et al., 1989b). The pitch angle in the mode becomes smaller as the value of 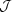decreases (panels (a), (b), and (c), respectively). For the case where 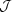and Q are large (panel (a)), the bar mode becomes unstable. In the case of large 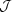but small Q (panel (d)), only the spiral mode is unstable. This behaviour is in agreement with that expected from the BLL dispersion relation (right panel in Figure 8). The right panel in Figure 8 shows curves of constant pitch angle α in the (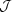, Q)-plane. The pitch angle here (for the more general definition see Eqn 27) is given by

(25)

where k_R and k_φ are the radial wave-number and azimuthal wave-number, respectively. Thus, the unstable spiral mode is determined by two parameters, 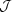and Q, given by the rotation curve of the galaxy disc. 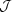controls the shape and growth rate of the unstable mode. The spiral mode appears for smaller 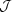, and the bar mode for larger 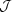(Lau & Bertin, 1978).

Figure 8. Left: Density contours of global unstable modes for a rotating fluid disc where (a) = 0.604 and Q = 1.500, (b), = 0.538 and Q = 1.096, (c), = 0.492 and Q = 1.002, and (d) = 0.858 and Q = 1.004. Right: Curves of constant pitch angle α = cot-1 kφ / kR in the (,Q)-plane. These curves are derived from the BLL dispersion relation (Equation 21) for the neutral stability condition (Equation 24) with Γ = 0 (flat rotation curve). From Bertin et al. (1989b).

The number of spiral arms and their pattern speed cannot be determined in the framework of the tight-winding density-wave theory of Lin-Shu-Kalnajs (Section 2.1.1). On the other hand, for global mode theory, if the unstable mode with the highest growth rate (trailing spiral modes) is assumed to be the spiral arms actually observed, then the spiral arms can be uniquely predicted from the equilibrium state of a galactic disc. Therefore, it turns out that global unstable mode theory is a self-contained theory.

However, there are some limitations in the global mode theory. Firstly, it is assumed that the spiral mode rotates as a rigid body, without changing its shape in the global unstable mode analysis. Iye et al. (1983) studied the global unstable modes of the fluid disc without the rigid-body rotation of the spiral modes, and reported the appearance of a global leading mode as well as global trailing modes, which is a different result from the rigid-body case (Aoki et al., 1979). Recently, N-body simulations also show that spiral arms wind up over time by the shear of the galaxy disc (Wada et al., 2011, Baba et al., 2013, Grand et al., 2013, see Sections 2.2.1 and 4.2 for details). Secondly, because global spiral modes grow up exponentially with time, the global mode theory requires self-regulated mechanisms such as damping effects in the stellar disc (e.g., Landau damping) and/or a gas component (Lin & Bertin, 1985, Bertin & Romeo, 1988, Bertin et al., 1989a, see also Section 3.1). Finally, it is unclear that the global modes really accomplish a neutrally stable state. The global mode theory hypotheses that the spiral arms are global neutral stability modes, which are accomplished by regulation mechanisms for the growth of density waves. However, Lynden-Bell & Kalnajs (1972) showed that spiral waves transport angular momentum by the gravitational torque which changes the distributions of angular momentum and mass (i.e., induces migration of stars and gas).

2.1.5. Simulations of long-lived spiral patterns

Various studies have tried to reproduce non-barred quasi-stationary density waves using numerical simulations, but so far, no convincing isolated, long-lived grand design spirals have been produced. The m = 2 case is of particular interest because low m modes are most likely to be stable (see Section 4.5), hence simulations have tended to focus on trying to model galaxies with a 2 armed spiral structure. As discussed in the previous sections, attaining a stable m = 2 perturbation involves modelling a disc which is sufficiently self gravitating to be unstable to the m = 2 mode, but stable to bar formation, and whereby density waves are able to be maintained by the presence of a Q barrier before the ILR, where waves can be reflected back towards corotation (Section 2.1.2). Two armed spirals associated with bars, or interactions, are of course common outputs from simulations, and we discuss these in Sections 2.3 and 2.4.

Early simulations of stellar discs all tended to form a bar (or oval distortion), and develop a strong m = 2 spiral mode (Miller et al., 1970, Hohl, 1971). The formation of a bar was also predicted analytically in the case of a uniformly rotating disc (Kalnajs, 1972, Kalnajs & Athanassoula-Georgala, 1974). However with the adoption of an extended, massive (comparable to or more massive than the disc) dark matter halo, the bar mode was both predicted, and found to be suppressed (Ostriker & Peebles, 1973, Hohl, 1976). Since then, simulations of isolated, non-barred galaxies have only produced multi-armed galaxies with transient spiral arms, as we discuss in Section 2.2. These types of galaxies can be produced readily with an N-body code. By contrast, trying to model an m = 2 spiral requires a long list of criteria to satisfy, and even then, m = 2 spirals still appear to be transient, evolving to m = 3 spirals and back again.

Thomasson et al. (1990), and also Elmegreen & Thomasson (1993), performed calculations of a galaxy, where in addition to the conditions above, they also enforced that the stellar velocity had to be maintained at a low value, and included a gas component. As will be mentioned in Section 3.2, and stated in Section 2.1.4, gas is likely required to allow energy from the spiral waves to dissipate. The galaxy tends to exhibit a pattern changing between 2 and 3 arms, and consequently has an asymmetric, rather than symmetric m = 2 pattern at many time frames. Without a Q barrier, the spirals are shorter lived, whilst without cooling or gas, higher m patterns become more prominent. Donner & Thomasson (1994) found similar results with a more consistent star formation scheme for the gas, and gas cooling and heating. Zhang (1996) used the same setup as Donner & Thomasson (1994), and found similar spiral patterns, but without including a gas component. As well as changing to a 3 armed pattern, spirals which transition between an m ≥ 2 spiral and a barred spiral are likewise feasible to simulate by including gas accretion (Bournaud & Combes, 2002). But as yet no simulated galaxy retains a steady m = 2 spiral.

Sellwood (2011) tested some of the models claiming to find m = 2 spirals. He performed N-body simulations designed to test directly whether a galaxy model corresponding to panel (c) of Figure 8 can in fact survive to support the slowly growing mode they predict should dominate. He argued that this model evolves quickly due to multi-arm instabilities originating from swing-amplified noise (see Section 2.2.1) instead of producing quasi-stationary, two-armed spiral modes. This result suggests that dynamical evolution associated with shearing of spiral arms which is not considered in quasi-stationary density wave theories is important for generating the spiral arms in real galaxies. Sellwood (2011) also tested some of the above models, which have proposed to exhibit long-lived spirals (Donner & Thomasson, 1994, Zhang, 1996). He showed that the bisymmetric spiral arm represented as a mode is not a single long-lived pattern, but the superpositions of three or more waves that each grow and decay.

Whilst simulations have been unsuccessful in reproducing a stationary spiral pattern, m = 2 or otherwise, recent work by D'Onghia et al. (2013) and Sellwood & Carlberg (2014) do report the existence of longer-lived 'modes', which survive multiple rotations, and thus more resemble density wave theory. However these authors still state that their results are inconsistent with the idea that spirals are quasi-stationary density waves because the arms in their simulations still fluctuate in time. By contrast in global mode theory we would expect the arm shape to be unchanging for a number of rotations. For these long-lived spiral arms, the disc is required to be fairly gravitational dominated (Sellwood & Carlberg (2014) adopt Q = 1) or include some perturbation(s) (D'Onghia et al. (2013), see also Salo & Laurikainen (2000b), Section 2.4.1).

2.2. Dynamic spirals

In this section we consider spiral arms which are transient, recurrent in nature. As we discussed in 2.2.1, the means of generating such arms is similar to that supposed in quasi-stationary density wave theory. However transient recurrent (or 'dynamic') spiral arms are much easier to form. For example dynamic arms occur readily in numerical simulations, where we can in relate predictions from swing amplification theory to the properties of the spiral arms generated, and in turn observations (see Section 4). Moreover stationary arms are in essence a small subset of arms resulting from gravitational instabilities requiring very specialised conditions in the disc to maintain the arms, whereas dynamic spiral arms can be generated with essentially any disc configuration that is not strongly bar unstable.

Pioneering N-body simulations of the stellar discs by Sellwood & Carlberg (1984) have shown that spiral arms are transient and recurrent structures (Carlberg & Freedman, 1985, Bottema, 2003, Sellwood, 2010b, Sellwood, 2011, Fujii et al., 2011, Grand et al., 2012b, Grand et al., 2012a, Baba et al., 2013, D'Onghia et al., 2013, Roca-Fàbrega et al., 2013). Sellwood & Carlberg (1984) argued that the spiral arms in N-body simulations generally fade out over time because the spiral arms heat the disc kinematically and cause the Q to rise. Thus, the disc becomes stable against non-axisymmetric structure (Section 2.1.1). They suggested that continuous addition of a kinematically cold population of stars is necessary to maintain the spiral arms. This suggests that the gas can effectively cool the system and thus play an important role (Section 3.1). Recently, Fujii et al. (2011) performed high resolution three-dimensional N-body simulations of pure stellar discs, and suggested that the rapid disappearance of the spiral arms may result from a low number of particles in previous simulations. Instead, they revealed a self-regulating mechanism that maintains multi-arm spiral features for at least 10 Gyr in a pure stellar disc (Figure 11).

Spiral arms in these N-body simulations are transient and recurrently reform. This is also the case for an N-body disc with a central bar (Baba et al., 2009, Grand et al., 2012b). The dominant spiral modes are time-dependent, reflecting a highly nonlinear evolution of spiral density enhancements, and radial changes (bottom panels in Figure 11). The arms are found to undergo a cycle - breaking up into smaller segments with typical sizes of a few kpc, then reconnecting by differential rotation to reform large scale patterns (Fujii et al., 2011, Wada et al., 2011). D'Onghia et al. (2013) presented a similar argument that the evolution of the spiral arm is characterized by a balance between shear and self-gravity of the galactic disc: the shear tends to stretch and then break the spiral arms locally, whereas in regions where the self-gravity dominates, the spiral arm is over-dense and generates the segments making up the spiral arms. Baba et al. (2013) pointed out that radial migration of stars around spiral arms are essential for damping of spiral arms, because excessive Coriolis forces originating from the growth of a spiral arm result in radial migration of the stars involved during the spiral arm evolution (their Figure 8).

In summary, these recent simulations of isolated disc galaxies conclude that the global spiral arms can appear to be long-lived visually, but they are assemblies of segments which break and then later reconnect with other segments of spiral arms. In this sense, the spiral arms are in 'dynamic equilibrium' between shear (or Coriolis force) and self-gravity rather than neutral stable waves assumed in the quasi-stationary density wave theory (Lin & Shu, 1964, Bertin & Lin, 1996).

2.2.1. Swing amplified spirals

We introduced swing amplification in Section 2.1.3 as a means of sustaining quasi-stationary density waves between the ILR and OLR. Here we describe the generation of dynamic spirals by swing amplification, but unlike the quasi-stationary density waves described in Section 2.1, there is no need for the waves to be reflected and maintained.

Full N-body simulations of stellar discs can test the predictions from swing amplification theory (Sellwood & Carlberg, 1984, Carlberg & Freedman, 1985, Bottema, 2003, Fujii et al., 2011, D'Onghia et al., 2013, Baba et al., 2013). We can estimate the dominating number of spiral arms, m, as

(26)

where X ≈ 2 (Equation 19) is assumed, and find this is roughly consistent with the results of N-body simulations. As described above, spiral arms typically develop most effectively when 1 < X < 2, so taking X ≈ 2 is appropriate (Figure 5). More generally, for a galaxy with a flat rotation curve (Γ = 0.5) and a total mass within the disc of M_tot (mainly dark matter and stars), since κ² = 2Ω² ∼ GM_tot / R², we also obtain the number of spiral arms as m ∼ Σ_tot / Σ₀ = 1 / f_disc. Carlberg & Freedman (1985) performed N-body simulations of galactic discs with various disc mass fractions and found that the number of spiral arms is strongly correlated with the disc mass fraction f_disc. A similar result is also obtained by N-body simulations with much higher resolution (Bottema, 2003, Fujii et al., 2011, D'Onghia et al., 2013). Also since κ = √2 Ω ∝ 1 / R for the galaxy with a flat rotation curve, m ∝ 1 / (RΣ₀) and the number of spiral arms tends to increase with radius in outer regions of exponential-discs. This agrees qualitatively with observations. As a specific example, we show the radial distributions of the number of spiral arms obtained by N-body simulations (Bottema, 2003) and observations of NGC 1288 (Fuchs & Möllenhoff, 1999) in Figure 9.

Figure 9. (top) Radial distribution of the number of spiral arms obtained by N-body simulations (Bottema, 2003). (middle) Same as the top panel, but for observations of NGC 1288 (Fuchs & Möllenhoff, 1999). (bottom) I-band face-on view of NGC 1288 (Fuchs & Möllenhoff, 1999).

The pitch angle of the spiral arm is in reasonable agreement with the predictions of swing amplification theory. Figure 10 shows the evolution of a stellar spiral arm along the pitch-angle - density-contrast (α - δ) plane. Due to differential rotation, one arm becomes more tightly wound as time goes by, and eventually disappears. In the meantime, new spiral arms with larger pitch angles start to grow. As the pitch angle of the spiral arm decreases from α ≈ 40^∘ (T_rot = 12.0) to α ≈ 32^∘ (T_rot = 12.20), the density contrast increases to a maximum, and the density contrast subsequently decreases with a decrease in the pitch angle. Thus, the spiral arm has a maximum amplitude when α ∼ 32^∘. This value is consistent with the expectation from swing amplification theory (hatched region in Figure 10). This behavior is similar to that reported in Sellwood & Carlberg (1984). We compare the pitch angles of spiral arms produced by swing amplification theory with observations in Section 4.2.

Figure 10. Evolution of spiral arm on α - δ plane for Trot = 12.0-12.5. The hatched region corresponds to the predicted maximum pitch angle around the analyzed region (Q ≈ 1.4 and Γ ≈ 0.8) due to swing amplification (refer to Equation (98) in Fuchs (2001)). From Baba et al. (2013).

In addition to the non-stationarity of stellar spiral arms, recent N-body simulations have shown that the pattern speed of the spiral arms decreases with radius in a similar manner to the angular rotation velocity of the disc (See also Section 4.1; Wada et al., 2011, Grand et al., 2012b, Grand et al., 2012a, Baba et al., 2013, Roca-Fàbrega et al., 2013). Thus, the spiral arms are considered to be rotating with the rest of the disc at every radius, and are material arms. In the above models, the evolution of the spiral arms is governed by the winding of the arms, which leads to breaks and bifurcations of the spiral arms. Sellwood & Lin (1989) and Sellwood & Kahn (1991) instead argued that the dynamics originate from multiple wave modes of different pattern speeds constructively and destructively interfering with one another (Sellwood, 2011, Quillen et al., 2011, Roškar et al., 2012, Sellwood, 2012).

Figure 11. Evolution of spiral arms with N = 30M. Top panels show the surface density, middle panels show the surface density normalized at each radius, and bottom panels show the Fourier amplitudes. From Fujii et al. (2011).

Finally, Sellwood & Carlberg (1984) also investigated the amplitudes of swing amplified spiral arms. They found that the growth of perturbations is in reasonable quantitative agreement with the prediction of swing amplification theory, although the growth factor was slightly larger than a naive expectation from the level of particle shot noise (i.e., swing-amplified noise). This discrepancy between numerical simulations and theoretical expectations is also seen in local stellar discs (Toomre & Kalnajs, 1991). It may relate to non-linear effects of swing-amplified spiral instabilities. Toomre & Kalnajs (1991) attributed the discrepancy to additional correlations between the particles that developed over a long period, i.e., the polarized disc response to random density fluctuations. By contrast, Sellwood (1989) showed that the amplitudes of spiral arms in global simulations of stellar discs seem to be independent of the particle number, rather than declining as N^-1/2 as would be predicted from the swing-amplified noise (Toomre & Kalnajs, 1991). It should be noted that star clusters and GMCs in real galaxies can seed much larger fluctuations than shot noise from equal-mass particles (D'Onghia et al., 2013). Sellwood (2011) also argued that spiral arms originating from swing-amplified shot noise are too low compared to observed spiral amplitudes. Instead, Sellwood (2000) suggested that spiral arms are vigorous large-scale modes originating from groove mode instabilities (Sellwood & Lin, 1989, Sellwood & Kahn, 1991) (see Section 2.2.3).

2.2.2. Corotation scattering and radial migration of stars

Since the dynamic spiral arms do not have a single pattern speed but roughly follow the galactic rotation, or multi-wave patterns with different pattern speeds exist, these arms scatter stars everywhere in the disc via the corotation resonance (Sellwood & Binney, 2002, Grand et al., 2012b, Roškar et al., 2012, Baba et al., 2013, Grand et al., 2014). Figure 12 shows the evolution of stars along the φ-R plane and the azimuth angle (φ)-the angular momentum (L_z) plane. The stars evolve in this plot due to changes in their angular momenta. When the stars are captured by the density enhancement (T_rot ≃ 11.8-12.0), they radially migrate along the spiral arms. The stars approaching from behind the spiral arm (i.e., inner radius) tend to attain increased angular momenta via acceleration along the spiral arm, whereby they move to the disc's outer radius. In contrast, the stars approaching ahead of the spiral arm (i.e., outer radius) tend to lose their angular momenta via deceleration along the spiral arm, and they move to the disc's inner radius. Along the φ-L_z plane, the stars oscillate both horizontally as well as vertically. Moreover, the guiding centers of the oscillations do not remain constant at the same value of L_z. This is essentially different from the epicycle motion in which L_z is conserved.

Figure 12. Orbital evolution of stars in the spiral arm. The stars associate around the spiral arm within a distance of ± 0.5 kpc at Trot = 4.0. Left columns: orbits on φ-R plane. Middle columns: orbits on φ - Lz plane. Right columns: orbits on E - Lz plane. The colors denote the angular momentum at the time instants when the stars are associated with the spiral arm. From Baba et al. (2013).

The panels in the right column of Figure 12 show the so-called Lindblad diagram, where the angular momentum L_z of each star is plotted against its total energy E. The stars oscillate along the curve of circular motion by undergoing change in terms of both angular momentum and energy (Sellwood & Binney, 2002, Grand et al., 2012a, Roškar et al., 2012, Baba et al., 2013). This is because stars around the corotation point change their angular momenta without increasing their random energy (Lynden-Bell & Kalnajs, 1972).

Grand et al. (2012a) also noticed the slight heating of negative migrators and the slight cooling for positive migrators (their Figure 12). Roškar et al. (2012), Minchev et al. (2012), and Baba et al. (2013) also reported a similar effect of the radial migration of stars around the spiral arms upon disc heating. Thus a non-negligible fraction of the particles that migrate outward have their orbits cooled by the spiral arm. This 'dynamical cooling' can be important for recurrent spiral instabilities.

2.2.3. Recurrent mechanisms for dynamic stellar spiral arms

The mechanism by which spiral arms recur is unclear. Sellwood & Kahn (1991), and Sellwood & Lin (1989) proposed a feedback cycle whereby narrow features in the angular momentum density of stars drive large-scale dynamic spiral arms. The arms in turn lead to resonant scattering of stars, which serves as a seed for the next spiral arm formation. This large-scale spiral instability, which originates from the deficiency of stars over a narrow range of angular momenta (also corresponding to a change in the surface density for stars on a circular orbit), is called the 'groove' instability. This feedback cycle was observed in N-body simulations of a low-mass disc with a near Keplerian rotation curve (Sellwood & Lin, 1989). The phase space density is depopulated near the OLR of one wave, inducing a new large-scale spiral instability with a CR near the OLR of the first wave. Sellwood (2000) also reported that the distribution of the solar neighborhood stars on in angular momentum phase space has similar fine structures (Sellwood, 1994, Sellwood, 2010a), suggesting that this recurrent mechanism cycle may occur in real spiral galaxies. Scattering of stars by spiral arms at the ILR, in such a way to form a new spiral arm, is also observed in more massive discs with near flat rotation curves (Sellwood, 2012). However, Sellwood (2012) concluded that some other mechanism may be required for recurrent spiral instabilities, because he was not able to find evidence to support the groove-type cycle such as observed in less massive discs with a near Keplerian rotation (Sellwood & Lin, 1989).

Baba et al. (2013) showed that oscillating stars successively undergo aggregation and disaggregation in energy-Lz space, thereby leading to the formation of structures referred to as 'swarms of stars' along the φ - L_z and R - φ planes (the right column of Figure 12). The non-steady nature of the spiral arms originates in the dynamical interaction between these swarming stars with a nonlinear epicycle motion, and the high-density regions, i.e., the spiral arms moving with galactic rotation. This is entirely different from what is expected in stationary density waves, where these changes are limited to the CR and Lindblad resonances (Lynden-Bell & Kalnajs, 1972). Thus, the gravitational interaction between the stars in the spiral arm and the spiral density enhancement changes the angular momentum and random energy of the stars, and this process in turn changes the structure of the spirals. During this process, the random energy of individual stars in the system does not increase monotonically. In other words, local interactions between the non-steady arms and stars increase or decrease the total energy of individual stars locally; however, the energy remains around its value for circular motion with the occurrence of a small dispersion. This is because the interaction causes the migration of the guiding centers of the stars without increasing their eccentricity or random energy. This 'dynamical cooling' mechanism (Grand et al., 2012a, Roškar et al., 2012, Minchev et al., 2012, Baba et al., 2013) is essential to preventing heating of the stellar disc and erasure of the spiral arms, and the mechanism produces 'swarms' of stars moving between non-steady spirals. The non-linear epicycle motion of the stars and their non-linear coupling with the density perturbation is the fundamental physics of the recurrently formed, non-steady spiral arms in a stellar disc.

2.3. Bar driven spirals

In many barred grand design spirals, the spiral arms start at the two ends of the bar. Two-armed spirals around strong bars are rather common, representing ≈ 70% of typical field spirals, unlike unbarred field spirals where only ≈ 30% are two-armed (Elmegreen & Elmegreen, 1982). Although this correlation suggests that the bar and spiral pattern have the same pattern speed and thus are related, the direct connection between bars and spirals is still unclear. There are three common interpretations (Mo et al., 2010): (1) the bar and spiral arms have a common pattern speed, (2) the bar and spiral arms have different pattern speeds and are independent patterns from each other, and (3) the bar and spiral arms have different pattern speeds but are coupled via some non-linear interactions.

2.3.1. Spirals corotating with bars

The first interpretation, which the bar and spiral arms have a common pattern speed, is intuitive from observations that most spiral arms connect to the ends of the bar. Sanders & Huntley (1976) studied the response of gas to a steady bar perturbation using hydrodynamical simulations. They found that the gas eventually settled into a steady state with a prominent trailing spiral structure. Gaseous spiral arms driven by a bar have since been seen in many further simulations (e.g. Schwarz (1981), Combes & Gerin (1985), Athanassoula (1992), Wada (1994), Englmaier & Gerhard (1999), Bissantz et al. (2003), Rodriguez-Fernandez & Combes (2008)). The gas arms are a direct response of the bar forcing. Figure 13 show the stellar closed orbits (left) and gaseous closed orbits (right) in a weak bar potential. Stellar orbits are always parallel or perpendicular to the bar, whilst the gas orbits change their orientation with radius, due to the effects of dissipation. The elliptical gaseous orbits are inclined to the bar potential in a trailing sense outside corotation. Thus, dissipation associated with the gas viscosity plays a critical role in driving gaseous spirals. Note that simulations in which a gas disc embedded in a 'steady' bar potential is replaced by a collisionless disc of test star particles also gives rise to a prominent trailing spiral structure but the stars never settle into a steady spiral structure. But stellar spiral arms can be excited by a 'growing' bar (Hohl, 1971).

Figure 13. Stellar closed orbits (left) and gaseous closed orbits (right) in a weak barred potential. The radii of the inner ILR, outer ILR, CR, and OLR are at 0.8, 2.4, 4.6, and 6.0, respectively. The gaseous closed orbits are calculated based on the damped orbit model by Wada (1994) who added the damping term (emulating the collisional nature gas) to equations of stellar orbits in a weak bar from Section 3.3 of Binney & Tremaine (2008). Note that Wada (1994) only showed a solution for radial direction. See the appendix of Sakamoto et al. (1999) for a full set of the solutions. A similar introduction of a damping term was also made by Sanders & Huntley (1976) and Lindblad & Lindblad (1994). The stellar response to forcing by a steady bar cannot form spiral arms. In contrast, the phase delay of epicycle motion in terms of the bar perturbation naturally takes place as does in a damped oscillator affected by a periodic external force. This phase delay determines direction of spirals (i.e. trailing or leading) around the Lindblad resonance (Wada, 1994).

Manifold theory or manifold flux-tube theory is proposed as a way of determining the orbits of stars in spiral arms driven by a bar (Romero-Gómez et al., 2006, Romero-Gómez et al., 2007, Athanassoula et al., 2009b, Athanassoula et al., 2009a, Athanassoula et al., 2010, Athanassoula, 2012, Voglis et al., 2006a, Voglis et al., 2006b, Tsoutsis et al., 2008, Tsoutsis et al., 2009). According to this theory, the backbone of barred spirals are bunches of untapped stars (so-called Lyapunov orbits) escaped from the unstable Lagrangian points ⁶, which are located on the direction of the bar major axis, outside the bar but near its ends. This means that, contrary to the quasi-stationary density waves, the stars do not cross the barred spiral arms but they move along them or they are spatially well confined by the manifolds ⁷ (Figures 1 and 4 of Athanassoula, 2012). Athanassoula et al. (2010) and Athanassoula (2012) compared the properties of spiral arms predicted by manifold theory with N-body simulations. They found good agreement between the manifold theory and the simulations (see Figure 12 of Athanassoula et al., 2010), and in the simulations stars moved along the spiral arms as predicted (see Figure 4 of Athanassoula, 2012). The manifold theory predicts that the relative strength of the non-axisymmetric forcing in the region around and beyond CR influences the winding of spiral arms, in the sense that in strongly barred galaxies the spirals will be more open than in less strongly barred ones (Athanassoula et al., 2010). This trend was corroborated in observed barred spiral galaxies (Martínez-García, 2012).

One observational indication of the bar-driven spiral scenario is that grand-design spirals are more frequent in barred galaxies than in unbarred galaxies (Elmegreen & Elmegreen, 1982). However there are still many multi-armed (e.g. NGC 1232, NGC 3344, NGC 3953, NGC 6946, IC 342, Figure 14), and flocculent (e.g. NGC 1313, NGC 5068) spirals that exhibit bars ⁸. Early type barred galaxies tend to have stronger bars and grand-design or multiple spiral arms, while late type barred galaxies have weaker bars and flocculent spiral arms (Fig.13 of Elmegreen et al. (2011)). Several studies have examined correlations between bar strengths and spiral arm strengths, with some finding clear evidence of bar driven spirals (Block et al., 2004, Salo et al., 2010), and others finding little or no evidence (Seigar & James, 1998, Durbala et al., 2009, Kendall et al., 2011). Thus observations suggest that the bar-driven spiral scenario is not necessarily valid for all barred spiral galaxies.

2.3.2. Decoupling between spirals and bars

The second possibility is that bars and spiral arms can be independent patterns. In this case, spirals in barred galaxies are associated with a spiral density wave, but probably with a pattern speed different from that of the bar (Sellwood & Sparke, 1988, Rautiainen & Salo, 1999). Indeed, Sellwood & Sparke (1988) have demonstrated N-body simulations of a stellar disc, and shown that multiple pattern speeds are quite common in disc galaxies, with the spiral structure typically having a much lower pattern speed than the bar. In other words, bars and spiral arms can be independent features. This implies a more or less random distribution of the phase difference between the bar and the start of the spiral arms, which seems to be in conflict with observations. However, as pointed out by Sellwood & Sparke (1988), contour plots of the non-axisymmetric density in their simulations show that the spiral arms appear to the eye to be joined to the ends of the bar for most of the beat frequency. This suggests that the observed correlation between bars and spirals might simply be an illusion.

2.3.3. Non-linear coupling between spirals and bars

A third interpretation for the origin of spiral arms in barred galaxies is a non-linear coupling between bars and spiral density waves, where the bar and spiral arm have different pattern speeds (Tagger et al., 1987, Sygnet et al., 1988, Masset & Tagger, 1997, Minchev et al., 2012). This mechanism assumes some small overlap between the corotation (CR) of the bar and the inner Lindblad resonance (ILR) of the spiral density wave. Using the tight-winding and epicyclic approximations for density waves, Tagger et al. (1987) and Sygnet et al. (1988) showed that this overlap enables the transfer of energy and angular momentum between the bar, spiral density wave and beat (m = 0 and m = 4) waves. The bar is stabilized at a finite amplitude by transferring energy and angular momentum to the spiral density wave, and the non-linear coupling drives beat waves. This theoretical argument on the non-linear coupling was also studied by N-body simulations of stellar discs (Masset & Tagger, 1997, Rautiainen & Salo, 1999), where the predicted strong beat waves were observed. This scenario is similarly supported by more recent N-body/SPH simulations of galactic discs (Minchev et al., 2012). Notably though, the derived beating waves exhibit chaotic behaviour rather than a stationary spiral pattern.

Sometimes the spiral arms do not start from the ends of the bar but exhibit a clear phase difference (e.g., NGC 1365). Similarly, some observed barred galaxies, such as NGC 3124 (Buta et al., 2007, Efremov, 2011) and NGC 3450 (Buta et al., 2007), show the curved, leading ends of the stellar bar (Figure 14). Similar morphology can be seen in N-body simulations of barred galaxies due to the oscillations between trailing and leading ends of the bar (e.g. Fux (1997), Rautiainen & Salo (2000), Martinez-Valpuesta & Gerhard (2011)). Martinez-Valpuesta & Gerhard (2011) suggested that the oscillations could be related to the oscillations seen in the bar growth in N-body simulations (e.g. Dubinski et al. (2009)) through angular momentum transfer to disc stars (e.g. Sellwood (1981)) and to non-linear coupling modes between the bar and spiral density wave as mentioned above.

Figure 14. B-band images of NGC 3953 (left), NGC 3124 (middle) and NGC 3450 (right). From The de Vaucouleurs Atlas of Galaxies (Buta et al., 2007).

2.3.4. Non-stationary spiral arms in barred galaxies

Grand et al. (2012b) performed N-body/hydrodynamic simulations of a Milky Way-sized barred galaxy and analyzed the spiral pattern speed. They found that the spiral arms are transient features and their pattern speeds decrease with radius in a similar manner to the angular velocity, but the pattern speed is slightly higher than the angular velocity of the disc. These results suggest that spiral arms in barred galaxies could be neither rigid-body rotating patterns predicted by the quasi-stationary density wave theory nor independent features, but transient features boosted by the bar. The non-stationarity of spiral arms in barred galaxies is also reported by other N-body/hydrodynamics simulations (Fux, 1997, Baba et al., 2009). Baba et al. (2009) argued that non-stationary, winding spiral arms in a simulated barred spiral galaxy originate via swing amplification (Section 2.1.3). In contrast, Roca-Fàbrega et al. (2013) reported that simulated spiral arms in strongly barred galaxies have a pattern speed almost constant in radius. More interestingly, they reported that the spiral pattern speed is close to disc rotation only when the bar is weak, as obtained by Grand et al. (2012b), but becomes almost constant when the bar has fully formed. These results suggest that the relation between bars and spiral arms can change during the evolutionary stages of bars, although there is no observational evidence to support, or contradict this picture.

2.4. Tidal interactions

2.4.1. Historical overview

Tidal encounters are frequent across all astronomy, with interacting galaxies providing some of the clearest examples. Early attempts to categorise interacting, and other more unusual galaxies, showed many examples of galaxies with tidal tails, bridges and clear spiral structure (Vorontsov-Velyaminov, 1959, Arp, 1966) prompting the morphology of galaxies to be associated with tidal effects (e.g. van den Bergh (1959), Lindblad (1960), Hodge & Merchant (1966), Toomre (1969)). The idea that tidal interactions may be responsible for spiral arms was in fact first demonstrated 20 years earlier, by Holmberg (1941). In a now famous experiment, Holmberg (1941) modelled the interaction of two galaxies by representing the galaxies by a series of lightbulbs. The lightbulbs have initial velocities associated with them due to the initial velocities of each galaxy assumed for the interaction, and their rotation curves. A photocell is used to measure the total amount of light at any particular point in the galaxies. Since light obeys a inverse square law the same as gravity, the total light received by the photocell is equivalent to the total gravitational force at that point in the galaxy. This force, or rather acceleration, is then used to calculate how far to move the given lightbulb. This step is then repeated for all the lightbulbs used, and the whole process repeated for many steps. The results of this experiment showed clearly the development of tidal spiral arms.

From the 1960s, actual numerical calculations of interacting galaxies were able to be performed (Pfleiderer & Siedentopf, 1961, Pfleiderer, 1963, Tashpulatov, 1970, Toomre & Toomre, 1972, Eneev et al., 1973), although they were still limited to test particle simulations using a restricted 3 body approach, which neglects stellar self gravity. These simulations focused mainly on the origin of tails and bridges in galaxies, rather than spiral arms themselves. Nevertheless, Toomre & Toomre (1972) still represents one of the most comprehensive studies of galaxy interactions, spanning over all possible alignments of the two galaxies in space, unequivocally showing that bridges and tails were indeed the result of tidal interactions. These simulations also reproduced a number of known systems remarkably well, including M51 and the Mice.

2.4.2. Tidally induced arms: stationary, kinematic or material arms?

Since the 1970s, full N body simulations, were able to model interactions with much higher resolution, and demonstrate that tidal interactions could account not only for tails and bridges at large galactic radii, but also spiral arms penetrating to the centre of a galaxy (Hernquist, 1990, Sundelius et al., 1987, Donner & Thomasson, 1994, Salo & Laurikainen, 2000b, Dobbs et al., 2010) (see Figure 15, left panel). Whilst these studies clearly demonstrate m = 2 spiral arms, a more critical question is whether the spiral arms are representative of the quasi-stationary spiral arm picture, are kinematic density waves, or material arms. For material arms there is no difference between the spiral arms and the underlying differential rotation of the stellar disc - the pattern speed of the arms is that of the disc, i.e. Ω_p(R) = Ω(R). Whilst material arms may describe the outer arms, or tidal tails of galaxies (e.g. Toomre (1969), Meidt et al. (2013)) they are not found to characterise the arms over the main part of the stellar disc. Sundelius et al. (1987) demonstrated using numerical simulations that tidally induced spiral arms are density waves rather than material arms, whilst observations have shown that the velocity fields of interacting galaxies do not correspond to material arms (e.g. Rots & Shane (1975)).

Figure 15. Simulation of M51 (left panel) showing the present day appearance of the galaxy, the orbit (dashed line) and the position of the perturber (white dot). The pattern speeds of the two spiral arms are shown on the right hand panel, with error bars (dotted lines). The angular velocity of the stars is also shown (red dashed line) and Ω ± κ/2 (blue dashed lines). From Dobbs et al. (2010).

Secondly the arms may be kinematic density waves. Kinematic density waves are not actually waves, in the sense that they don't propagate through the disc, and have zero group velocity. But gas and stars do flow through the arms, although unlike quasi-stationary density waves, the spiral pattern is not fixed. For purely kinematic density waves, self gravity of the stars can be ignored (kinematic density waves can be induced even when Q = ∞), the stars behaving simply as test particles. The influence of a perturber can be treated by the impulse approximation, and induces elliptical stellar orbits. Such orbits are not generally closed, but we can choose an angular speed such that the orbit is closed. For an m = 2 perturbation, we can choose a rotating frame such that the orbit is closed after half the epicylic frequency (or after each time an arm is encountered) i.e.

(27)

to a first order approximation (see Binney & Tremaine (2008)). If the orbits are aligned along the same major axis, then the perturbation produces a bar. If however, the orbits are offset as a function of radius, then they naturally produce a spiral pattern (Kalnajs, 1973). Increasing the offset makes the spirals more tightly wound. In the case of a moving (prograde) perturber, the orbits are not aligned, and a trailing spiral pattern develops with a pattern speed given by equation 24 (trailing since Comment 39: Ω(R) - κ(R) / 2 < Ω). The aphelia of the ellipses corresponding to the densest parts (arms) in the disc. Calculations of a perturber passing a galaxy in the non self gravitating case by Oh et al. (2008) demonstrate that the induced arms do indeed exhibit this pattern speed. Thus the pattern speed decreases with radius, but less so than the material arms case. The locations of the spiral arms can also be determined analytically, by applying the impulse approximation to the stellar orbits, and computing the Jacobian matrix from the derivatives the resultant orbit equations (Struck-Marcell, 1990, Donner et al., 1991, Gerber & Lamb, 1994, Appleton & Struck-Marcell, 1996). The surface density of the response to a tidal perturbation is then

(28)

(Gerber & Lamb, 1994) where R₀ is the original (unperturbed) radius of the (circular) orbit and J is the Jacobian. The points where J = 0 are caustics, and correspond to the locations of the induced arms.

Alternatively the spiral arms may be quasi-stationary density waves. In the self gravitating case, the effect of self gravity is to make the spiral pattern more rigid, increasing Ω_p. Swing amplification may also act to enhance the density of the arms still further. However it is not established whether self gravity is sufficient to make the spiral pattern fully self gravitating, and develop into a quasi-stationary density wave. Both Oh et al. (2008), and Dobbs et al. (2010) find that although the pattern speed is higher in their models than given by Equation 27, and decreases less with radius, the arms are not completely rigid and still wind up with time (see Figure 15, right panel). Sundelius et al. (1987) also find the development of spiral density waves in the absence of swing amplification, whilst Oh et al. (2008), and Dobbs et al. (2010) find swing amplification only has a minor effect. Salo et al. 2000 also find that the pattern speed is radially decreasing and again slightly higher than given by Equation 27, and again generally suppose that swing amplification has only a minor role in generating the arms. They do however find a more constant pattern in the centre kpc or so of their simulation of M51, and suppose that here Lin-Shu-Kalnajs (LSK) waves operate, the lack of an ILR in their simulation meaning waves can penetrate to the centre without being absorbed (in a number of their models, a bar forms in the centre, similar to the actual M51).

Overall the nature of spiral arms in tidally interacting galaxies likely represent the behaviour of the underlying disc. Galaxies with dynamic spiral arms likely do not exhibit fixed spiral patterns when tidally interacting as they are not gravitationally dominated. Galaxies with more massive discs, and likely bars, may well exhibit fixed patterns, at least in the central gravitationally dominated regions.

2.4.3. Prograde and retrograde encounters, and the orbit of the perturber

In addition to the nature of the spiral arms induced, we can also consider how the orbit of the perturber affects the tidal perturbation. The simulations of Toomre & Toomre (1972), and later Howard et al. (1993) demonstrated that retrograde encounters have a relatively small effect on a galactic disc, whereas prograde encounters are very effective at producing spiral arms, naturally of a trailing nature. Other analysis showed that tidal interactions could produce a leading spiral pattern, with one predominant leading arm (Kalnajs, 1971, Athanassoula, 1978, Thomasson et al., 1989). For the prograde case, as discussed earlier with respect to kinematic density waves, the angular speed of the perturber at closest approach during its orbit will likely be nearest to the Inner Lindblad resonance (Ω(R) - κ(R) / 2), and hence particularly effective at inducing an m = 2 perturbation. For the retrograde case, the angular speed exhibits the opposite sign, has little correspondence to any resonance (Toomre, 1969), but will likely be closest to an m = 1 perturbation (Ω_p = Ω(R) - κ(R)) corresponding to one leading (generally κ(R) > Ω(R)) arm (Byrd et al., 1989). Leading spiral arms are found to be rare in simulations, requiring a strong perturbation, and a large halo mass (Thomasson et al., 1989). The latter is important to prevent swing amplification, which would convert any leading perturbation into a trailing one. Observationally, NGC 4622, a ring galaxy, is the only galaxy found to exhibit leading spiral arms (Buta et al., 1992, Buta et al., 2003).

Various simulations have also investigated the impact on the galaxy from perturbers of different masses (Byrd & Howard, 1992, Oh et al., 2008, Struck et al., 2011). The simulations find that a perturber typically needs to be at least 0.01 times of the mass of the main galaxy to have an effect, ideally closer to 0.1 times the mass to produce a clear grand design pattern, although naturally there is a degeneracy with the pericenter of the orbit (Oh et al., 2008). Toomre & Toomre (1972) showed that a perturbing galaxy has greatest impact when orbiting in the plane of the main galaxy, but changing the angle of inclination of the perturbing galaxy has little qualitative effect.

Another factor determining the dynamics of tidally induced spirals is the number of orbits of the perturber, and thus whether it is bound. For M51, the best matched orbit of M51 and NGC 5195 currently involves two orbits of the NGC 5195 around M51, after which the two galaxies merge (Salo & Laurikainen, 2000a, Theis & Spinneker, 2003). Consequently the dynamics are quite chaotic, whilst the orbit induces different sets of spiral arms resulting in noticeable kinks along the spiral arms as observed today (Salo & Laurikainen, 2000b, Dobbs et al., 2010). The spiral arms consequently show clear departures from logarithmic spirals. Oh et al. (2008), and Struck et al. (2011) present simulations where a perturber is on an unbound orbit, and passes the galaxy only once. In this case, the dynamics are less chaotic, and the arms smoother.

2.4.4. Longevity of tidally-induced spirals

If m = 2 spirals are difficult to produce except by tidal interactions or bars, as we conclude from Section 2.1.5, their lifetime is an important characteristic. Grand design m = 2 spirals are common, hence tidal interactions must induce relatively long-lived spiral arms if they are the main source of such galaxies.

Assuming their pattern speed is not fixed, tidal arms are expected to have a pattern that winds up slower than local transient arms discussed in the previous section, but to be shorter lived than quasi-stationary spiral arms. For tidally induced spiral arms, there are two main questions regarding how long they last. The first is how much they wind up over time, the second is how long the arms take to decay or damp. To think about the first issue, we can consider the pitch angle of the arms, defined as the angle between the tangent of the spiral arm and a circle, i.e.

(29)

where the derivation is evaluated along the spiral arm. If we consider the change in φ at a later time as φ(R, t) = φ₀ + Ω_p(R)t then the pitch angle can be written as:

(30)

(Binney & Tremaine, 2008). For material arms, Ω_p = Ω and for a flat rotation curve of v_c = 200 km s^-1, the pitch angle will be ∼ 1^∘ after about 1 Gyr. This is considerably lower than observed pitch angles. For material arms, the pattern winds up on a timescale of order t ∼ |dR / (R dΩ)| = 1 / |dΩ / dlnR|, in the above example 100 Myr.

For kinematic tidal arms, in the absence of self gravity, Ω_p(R) = Ω(R) - κ(R) / 2 (Section 2.4.1), and so |dΩ_p / dlnR| ≪ |dΩ / dlnR|. Hence the spiral pattern is expected to last somewhat longer. In the presence of self gravity, Ω_p versus R can become even shallower. For example, if we take Figure 15 (right panel), in 1 Gyr, the pattern winds up at a rate ∼ 4 times slower than the above example for material arms, and is expected to have a pitch angle of 5 or 6^∘ after 1 Gyr. These values are, as would be predicted, at the lower end of observed values (Seigar & James, 1998, Seigar et al., 2006).

Simulations of tidally induced spiral arms confirm this behaviour, with the pattern winding up and simultaneously decaying on a timescale of ∼ 1 Gyr (Oh et al., 2008, Struck et al., 2011). Similar to the case of dynamic spiral arms (Section 2.2), Struck et al. (2011) also found that the arms persisted for longer with higher resolution simulations. Struck et al. (2011) also supposed that galaxy encounters in groups and clusters are likely frequent, and with spiral arms persisting for ∼ 1 Gyr, tidally induced spiral galaxies common.

2.5. Stochastic star formation

The idea of the generation of spiral arms by stochastic self-propagating star formation (SSPSF) was developed principally by Mueller & Arnett (1976), and Gerola & Seiden (1978). Each generation of star formation is presumed to trigger new star formation in neighbouring regions, by the production of shocks from supernovae winds. Then, due to differential rotation, the newly formed stars are sheared into material spiral arms. Like the picture of Goldreich & Lynden-Bell (1965a), the spiral arms are new stars, but in their case the spiral arms were associated with gravitational instabilities in the gas, rather than supernovae. This mechanism is not supposed to account for grand design galaxies, but tends to produce flocculent spiral arms (Gerola & Seiden, 1978, Jungwiert & Palous, 1994, Sleath & Alexander, 1995). Spiral arms are not long-lived in this model, rather they are continually created and destroyed.

The conclusion of these studies is that SSPSF is a secondary effect, rather than a primary means of generating spiral arms. In general, stellar discs in observed galaxies are not smooth, spiral structure is seen in the old stellar population, which is much amplified by the response of the gas. In fact, Mueller & Arnett (1976) concluded that stochastic star formation would not produce global spiral structure, but rather in conjunction with other mechanisms, such as density waves, would add an irregular structure to the galaxy. For example supernovae and triggered star formation are likely to help produce much wider spiral arms in tracers such as HI, CO and Hα than expected from the gas response to a spiral shock. In the absence of feedback, the width of spiral arms is too narrow compared to observations (Douglas et al., 2010).

Local regions of likely SSPSF have been observed mostly in the LMC (Westerlund & Mathewson, 1966, Feitzinger et al., 1981, Dopita et al., 1985, Kamaya, 1998). In particular SSPSF seems most successful in irregular galaxies (Hunter & Gallagher, 1985, McCray & Kafatos, 1987, Nomura & Kamaya, 2001), which are not dominated by rotation, or other mechanisms for producing spiral structure. Direct triggering of molecular cloud formation by supernovae has been suggested observationally, for higher latitude regions in the Milky Way (Dawson et al., 2011), and in the LMC (Dawson et al., 2013). However there is little evidence that SSPSF is a global driver of spiral arms. After the 1980s interest in SSPSF appears to have waned. It is now feasible to perform hydrodynamical models of galaxies, including stellar feedback. These seem to indicate that instabilities and collisions dominate star formation in spiral galaxies, unless the level of feedback is unrealistically high (Dobbs et al., 2011).

2.6. Exotic mechanisms

An alternative means of generating spiral arms, aside form gravitational instabilities in the stellar disc or tidal interactions with visible perturbers, is from asymmetries in the dark matter distribution. This may take the form of gravitational instabilities induced by asymmetries in the dark matter profiles of galaxies (Khoperskov et al., 2013), or tidal perturbations from dark matter sub halos (Tutukov & Fedorova, 2006, Dubinski et al., 2008, Kazantzidis et al., 2008, Chang & Chakrabarti, 2011). For the latter case, although the masses of the sub halos are assumed to be small (∼ 10⁶ M_⊙), they are extremely close to, if not passing through the galactic disc during their orbits. Cosmological simulations predict a multitude of sub halos, albeit with a greater frequency than observed. The effect of dark matter sub halos is thus at present entirely speculative. Simulations predict that the impact of such halos should be detectable (Dubinski et al., 2008, Chang & Chakrabarti, 2011), but whether such effects are distinguishable from other perturbations (e.g. non-dark matter perturbers, previous low mass mergers, bar instability, gravitational instabilities) is an open question.

¹ Named after the Wentzel-Kramers-Brillouin approximation of quantum mechanics. Back.

² A physical interpretation of Q arises from comparing the timescale for gravitational collapse ∼ (λ / G Σ₀)^1/2 to those for shear, ∼ 1 / κ and pressure (∼ λ/c_s). Requiring that a region size λ collapse on a timescale shorter than the time for shear or pressure to react leads also to Q as for Equation 7, but without the numerical denominator (Pringle & King, 2007). Back.

³ Here 'standing' means that the density waves do not propagate radially but do propagate azimuthally with a pattern speed. Back.

⁴ Lynden-Bell & Ostriker (1967) have proved the so-call anti-spiral theorem which argues that there is no neutral spiral mode unless there exists degeneracy of modes or dissipation mechanism. Back.

⁵ Although the LS dispersion relation (Equation 4) is derived by the tight-winding approximation, i.e., |R k_R| ≫ 1, the BLL dispersion relation (Equation 21) is derived by an asymptotic analysis based on the following ordering: є₀² ≪ 1 and (k / k_crit)² = (1). Thus even very long waves with |k_R| ≪ 1 can be described by means of a WKB treatment of the gravitational potential, provided the quantity m² is taken to be formally large. See Bertin (2000) for more details. Back.

⁶ The direction in which the (chaotic) orbit can escape from the unstable Lagrangian points is not all direction but is set by the invariant manifolds. Manifolds can be thought of as tubes that guide the motion of particles whose energy is equal to theirs (Romero-Gómez et al., 2006, Athanassoula et al., 2009b). Back.

⁷ Although, there is another view of the manifold theory: the locus of all points with initial conditions at the unstable manifolds that reach a local apocentric (Voglis et al., 2006a, Voglis et al., 2006b, Tsoutsis et al., 2008, Tsoutsis et al., 2009) or pericentric (Harsoula et al., 2011) passage, but the details are beyond the scope of this review. Back.

⁸ though the latter seem more difficult to find. Back.