


Although not yet conclusive, there are a growing number of observational tests for whether galaxies display quasi-stationary density waves, tidally induced or bar driven spirals, or instability induced dynamic spiral arms. Most of the observational tests relate to the pattern speed of the spiral arms, and whether the distribution of gas and stars match the predictions for a fixed pattern speed or not. Only the quasi-stationary density wave picture adopts a constant pattern speed, whilst the other mechanisms induce arms with radially decreasing pattern speeds.
The pattern speed is difficult to measure directly, but there have been many attempts to estimate pattern speeds in galaxies. Most measurements have assumed that the pattern speed is constant, thereby immediately adopting the assumption that the spiral pattern is a quasi-stationary spiral density wave. The simplest means of determining the pattern speed is to estimate the location of corotation (e.g. assumed coincident with the outer extent of the arms, or a dip in HI or CO at a certain radius Shu et al., 1971, Rots, 1975, Elmegreen et al., 1989, Sempere et al., 1995). Supposed locations for the ILR (e.g. assumed coincident with the inner extent of the spiral arms, rings or inter arm features) and/ or the OLR can be similarly used to estimate the pattern speed (Lin & Shu, 1967, Gordon, 1978, Elmegreen et al., 1989). These methods suffer from uncertainties, both observationally and theoretically about where spiral arms begin and end (see e.g. Contopoulos & Grosbol (1986), Elmegreen et al. (1998), Englmaier & Shlosman (2000)), and of course whether these really are resonance features.
Another indirect test of the pattern speed is the location of the spiral shock, and star formation relative to the minimum of the stellar potential. For a fixed spiral pattern, the spiral shock will lie one side of the minimum of the stellar potential within corotation, and the opposite side outside corotation. The width of this offset can be used to determine the pattern speed, if a constant sound speed is assumed. Gittins & Clarke (2004) demonstrated this method using numerical simulations, where they presumed the spiral shocks will correspond to dust lanes. Likewise, assuming a timescale for star formation to occur, the molecular clouds (CO) and Hα will have a predicted offset. Egusa et al. (2004) used this prediction to derive a constant pattern speed for NGC 4254, following which they are able to derive pattern speeds for 5 out of a sample of 13 galaxies (Egusa et al., 2009). Difficulties in obtaining pattern speeds for many spirals, and the large scatter with this method, likely arise because the spirals are transient, and the offsets local and non-systematic. Tamburro et al. (2008) instead measured offsets between atomic hydrogen and recent star formation (24 µm maps) to simultaneously fit Ωp and the star formation timescale for M51, the latter found to be 1-4 Myr. Repeating their analysis however, Foyle et al. (2011) found no evidence for a systematic offset, and thus a constant pattern speed. One difference may be that Foyle et al. (2011) try to fit a pattern speed over the entire galaxy, whereas Tamburro et al. (2008) studied localised regions. Such differences indicate the large uncertainties in observationally determining the behaviour of spiral arms, and that the assumption of a constant pattern speed may be invalid.
As well as using morphological features of spiral galaxies to determine corotation, the kinematics can also be used, either from the residual velocity fields or changes in the directions of streaming motions (Canzian, 1993, Sempere et al., 1995, Elmegreen et al., 1998). Canzian (1993) showed that the spiral residual velocity field shows a single spiral feature inside corotation, and 3 spiral features outside corotation. Font et al. (2011) also used the velocity field to determine the location of resonances from the locations where the residual velocities are zero, from high resolution Hα data.
So far all the methods described assume that the pattern speed is constant. The (Tremaine & Weinberg, 1984) method uses the continuity equation for gas flow across the spiral arms, which relative to the rest frame, and integrating over each direction, gives an expression of the form
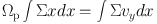 |
(39) |
(Merrifield et al., 2006). Here, Σ, vy and x are all observables (of the relevant tracer) which means Ωp can be determined. For the continuity equation to be valid, this method tends to use HI or CO to avoid problems with extinction, although a small fraction of the gas will be turned into stars. The Tremaine-Weinberg method also assumes a steady state, i.e. that the spiral arm is not changing over the timescale that gas passes through the arm, and assumes a thin disc, but is in principle not limited by the shape of the arm.
This technique has been used mainly for barred galaxies, due mainly to the simpler geometry, but also for a number of spiral galaxies (Sempere et al., 1995, Zimmer et al., 2004, Rand & Wallin, 2004). The method can be extended to allow for a radial dependent pattern speed (Westpfahl, 1998, Merrifield et al., 2006). In this case, the pattern speed can be determined by solving a matrix equation over different positions within a small (e.g. 0.5 kpc width) region along a spiral arm. The pattern speed is then computed for other regions at different radii. Using this method, a number of studies have found radially decreasing pattern speeds (Merrifield et al., 2006, Speights & Westpfahl, 2011, Speights & Westpfahl, 2012) including for M81 (Westpfahl, 1998). Meidt et al. (2008b), Meidt et al. (2009) also found radial dependent pattern speeds in M51, M101 and a number of other galaxies, but attributed these to different patterns with different pattern speeds at different radii, rather than a continuously decreasing pattern speed. Differences in pattern speed are likely at the transition from a bar to spiral arms (e.g. Meidt et al. (2008b), see also Section 2.3), but this would not explain discrete changes in pattern speed at larger radii, or in the absence of a bar.
To date, no examples of galaxies with a constant pattern speed have been found with the radially varying Tremaine-Weinberg method. Most galaxies show a slowly decreasing pattern speed in the outer regions. The Tremaine-Weinberg method appears sufficient to establish that patterns speeds vary radially (i.e. the pattern speed varies much more than the error bars), but not whether the pattern speed varies continuously or consists of multiple segments each rotating at a constant pattern speed (Meidt et al., 2008b, Meidt et al., 2008a).
We can also consider whether the pitch angles of spiral arms of observed galaxies match predictions from models and theory. Grand et al. (2013) analyzed the pitch angles of transient stellar spiral arms in galaxy models with different shear rates (Γ), and showed that the higher shear rates produce more tightly wound spiral arms. It is also clear that the pitch angle of the spiral arms decreases with time. Figure 19 shows the pitch angles of simulated spiral arms plotted against the shear rate of model galaxies. The observed correlation of real spiral galaxies are also overlaid on this figure. This trend and scatter are both consistent with the observations (Seigar et al., 2005, Seigar et al., 2006). Though spiral arms wind up by differential rotation, typical pitch angles depend on the shear rate of disc galaxies suggesting that swing amplification is important for generating spiral arms because swing-amplified spiral arms reach maximum amplitudes at a specific pitch angle depending on the shear rate (Section 2.1.3 and Figure 10).
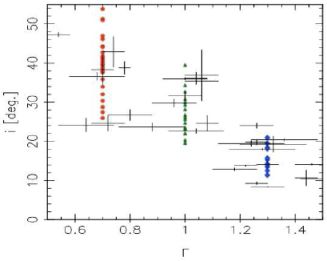 |
Figure 19. The pitch angle is shown versus shear, from Grand et al. (2013). The coloured points represent simulated values taken from Grand et al. (2013), whilst the crosses are observed values, from Table 3 of Seigar et al. (2006). |
The quasi-stationary density wave theory may also satisfy the pitch angle-shear rate correlation qualitatively (Lin & Shu, 1964, Roberts et al., 1975), since Lin & Shu (1964) demonstrated that the pitch angle of quasi-stationary density waves is lower for higher central mass concentration, i.e., a higher shear rate. Observations by Block et al. (1994) support the scenario that spiral arm properties are intrinsic to a galaxy dependent on galaxy morphology and gas content (see also Section 4.5).
The ages of stellar clusters can also be used as a test of the underlying dynamics in galaxies. This method was described in Dobbs & Pringle (2010). The ages of clusters should clearly increase with distance away from the spiral arm (in the leading direction) for a constant pattern speed. Likewise a similar pattern is expected for a bar. However for the case of dynamic spiral arms due to local instabilities there is no flow of material through the spiral arms. Hence no age pattern is expected, rather stars of similar ages lie along a spiral arm (see Figure 20). The numerical models of Dobbs & Pringle (2010) were relatively simple, and did not include for example stellar feedback. More complicated models have since been performed by Wada et al. (2011) and Grand et al. (2012b), Grand et al. (2012a). They confirmed the case that for dynamic arms, there is no clear age pattern, testing multi-armed galaxies both with and without bars. Dobbs et al. (2014) extended this idea further by looking specifically at stellar age spreads in GMCs, and suggest again that different age distributions may reflect how the spiral arms are generated.
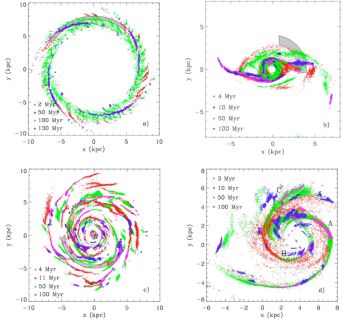 |
Figure 20. The spatial distribution of clusters of different ages is shown for different galaxy models: fixed spiral potential (top left), barred galaxy (top right), dynamic spiral arms (lower left) and a model of M51 (lower right). For the fixed potential and bar. there is a transition of stellar ages moving away from the spiral arms / bar. For the flocculent galaxy, star clusters of similar age tend to be located in a spiral arm, and the ages do not show clear transitions, rather they are more random. From Dobbs & Pringle (2010). |
Dobbs & Pringle (2010) also tested a model of M51, where they found that although the spiral arms are kinematic density waves, and there is flow of material through them, the dynamics of the interaction were rather chaotic and produced a chaotic distribution of stellar ages. Observations of stellar ages in M51 have since confirmed a similar picture (Foyle et al., 2011, Kaleida & Scowen, 2010, Chandar et al., 2011). Studies of galaxies undergoing less violent interactions have not been tested.
From the numerical models, the patterns for the dynamic spirals appear most robust, because the peaks in the number of stars corresponding to the arms are significantly higher than the noise (e.g. a factor of ∼ 10). For the case of the stationary density wave, the pattern is potentially more confusing, because the peaks in the number of young stars decrease and broaden away from the arm, so they are less distinct. Furthermore after a relatively short time (10s Myrs), the young stars will catch up with the next spiral arm.
Several observational studies have examined whether age patterns exist in a number of nearby galaxies (Sánchez-Gil et al., 2011, Foyle et al., 2011, Ferreras et al., 2012). With the exception of one or two galaxies e.g. M74, the observations generally find little evidence of age patterns. As well as stellar clusters, a number of studies have also used colour gradients across the spiral arms as a measure of a transition in stellar ages (Efremov & Ivanov, 1982, Regan & Wilson, 1993, Beckman & Cepa, 1990, Gonzalez & Graham, 1996, Martínez-García et al., 2009). However again, with the exception of one or two cases, there is rarely a clear trend in the colour gradients.
4.4. Resonances and interference patterns
As well as looking at the pattern speeds, or age spreads, it is also possible to look for specific features that result from the quasi-stationary density wave picture. Patterns of star formation along the spiral arms have been seen in some galaxies, and attributed to resonances, for example a dip in star formation at corotation (Cepa & Beckman, 1990, Knapen et al., 1992). As already mentioned, features associated with resonances are expected at certain radii in a disc. In a few galaxies, symmetric spurs, or breaks in the spiral arms are relatively convincing, e.g. NGC 1566 (Elmegreen & Elmegreen, 1990). Features such as outer rings due to bars can also be seen (e.g. Buta & Crocker (1991)). However in many cases subtle features associated with spiral arms may simply be due to the shearing of clouds, or bridges where spiral arms in the gas remain whilst corresponding features in the stars have dissipated (Section 3.7).
In the global model theory of spiral arms, see Section 2.1.4, the spiral pattern is thought to correspond to an interference pattern resulting from leading and trailing waves in the stellar disc. Elmegreen (1989) found some signs of leading waves for M51, M81 and M100, but equally the patterns they found could be simply due to the underlying complex structure of the disc.
4.5. Observations of grand design and flocculent structure
Any theory(ies) of spiral structure also need to explain the observed frequency of grand design and flocculent spirals. One of the arguments for quasi-stationary density waves has been the large number of galaxies with m = 2 spiral structure. In density wave theory, density waves with m > 3 are less likely to be stable (Lin & Shu, 1967, Toomre, 1977, Thomasson et al., 1990) compared with m = 2, explaining the preference for m = 2 spirals. An alternative explanation is that the m = 2 spirals are all tidally induced or bar driven. This hypothesis was made by Kormendy & Norman (1979), who found the majority of grand design galaxies had bars or companions. Some isolated galaxies exhibited arms which did not extend to the flat part of the rotation curve, which meant that they could potentially be longer lived spirals, as the winding problem is avoided. Other isolated grand design galaxies in their sample were thought to have undergone recent mergers.
Observations also show that the frequency of grand design galaxies doubles in clusters or groups compared to otherwise (Elmegreen & Elmegreen, 1983a). There are thus few isolated grand design galaxies, but even then, determining whether there are examples which could not be explained by tidal interactions is difficult, partly due to the difficulty of establishing truly isolated galaxies and those that have not undergone a recent merger (see e.g. Verley et al. (2007)). It is also not established either theoretically, or using cosmological simulations, whether interactions are likely to be frequent enough to account for the observed number of grand design spirals. As discussed in Section 2.4.4, spiral galaxies can be expected to retain m = 2 structure for ∼ 1 Gyr after an interaction.
One argument for the existence of long-lived spiral arms is the finding that some galaxies that appear flocculent or multi-armed in the optical exhibit an underlying grand design pattern in the old stellar population, i.e. as seen in the K band (Block & Wainscoat, 1991, Block et al., 1994, Block et al., 1996, Thornley, 1996, Thornley & Mundy, 1997, Grosbol & Patsis, 1998, Seigar et al., 2003). Whilst these structures could be tidally induced, Block et al. (1994) suggested that in fact the stellar disc supports low m modes whereas the gas (and young stars) does not since low m modes are damped at the ILR. Thus in this scenario the two components of the disc are assumed to be decoupled. Given that theory, and simulations, show that gas shocks at the spiral arms, presumably there is still some relation of the gas to the stars, many of the examples in Block et al. (1994) simply show an extra optical arm. An alternative scenario, in the dynamic arm picture is that these galaxies, which are sufficiently massive to exhibit only a small number of spiral arms, are transitioning between 2 and 3 armed patterns, and the features in the optical are remainders of spiral arms where the stellar pattern has dispersed, but the gas arm (which is clearly denser and colder) still persists. Chakrabarti et al. (2003) provided an alternative picture whereby resonances may be responsible for generating substructure from an underlying stationary m = 2 pattern, particularly for highly flocculent galaxies, although other means of generating substructure (e.g. instabilities, stellar feedback) may be just as likely responsible (see reference to Elmegreen et al. (2003) below). The most recent observations found that most flocculent galaxies do not exhibit grand-design structure (Elmegreen et al., 2011) and those that do have very weak spiral arms (Elmegreen et al., 1999), but the co-existence of different patterns still needs to be explained.
Conversely all galaxies may be flocculent galaxies, which merely develop an overwhelming m = 2 mode during tidal perturbations, or with a bar (Sections 2.3 and 2.4). Colombo et al. (2014) found evidence for an underlying flocculent spiral in the grand-design spiral M51, proposed for the old stars as well as the gas (CO). Elmegreen et al. (2003) suggested that both grand design and flocculent spirals (as seen in the old stars) exhibit a similar structure in the gas and young stars (independent of the underlying old stellar population) which is driven by turbulence in the disc.
The spiral structure of our Galaxy is reviewed thoroughly in Benjamin (2014), so we only briefly discuss the Milky Way here.
The number of spiral arms in our Galaxy is still debated somewhat (see e.g. Vallée (2005)), but is most frequently considered to be either 2 or 4. There are 4 main spiral arms; the Perseus, Sagittarius, Scutum-Crux, and Norma spiral arms, and at least one bar. There is in addition the Outer Arm, which may be the outer part of one of the inner arms, and the Local or Orion arm, which is much shorter, and may be a bridge or spur rather than a real arm.
A large number (m > 2) of arms would support the view that the Galaxy better resembles a flocculent, rather than grand design spiral, with multiple dynamic arms induced by local gravitational instabilities. An alternative interpretation is that the Galaxy has two main spiral arms (the Perseus and Scutum-Centaurus arms), with the other two arms lesser features, perhaps only present in gas and young stars (Drimmel, 2000). Such a scenario could arise in the quasi-stationary density wave picture if the secondary arms are resonance related features (Martos et al., 2004). In the Churchwell et al. (2009) map of the Galaxy, the secondary arms appear to start at the ends of the bar, and / or be connected with the inner 3 kpc arms, and the main arms also start at the bar.
As well as gravitational instabilities induced locally by perturbations in the stellar distribution, or GMCs, the Galaxy is surrounded by low mass companions, and contains one or two bars. Hence there is no shortage of mechanisms to generate spiral arms. Purcell et al. (2011) showed that a recent passage of the Sagittarius galaxy could have induced spiral arms, though their simulations did not show the detailed spiral structure. Either the bar(s) or interactions could lead to an m = 2 pattern. One of the most striking pieces of evidence that there is a symmetric m = 2 pattern, suggestive of Lin-Shu density wave theory is the recent discovery of an outer HI arm, which is found to match up exactly with the inner Sagittarius arm, assuming a continuous m = 2 logarithmic spiral pattern (Dame & Thaddeus, 2011). Some other models of the Galaxy tend to show kinked arms, rather than continuous spiral arms (e.g. Taylor & Cordes (1993)).
Numerical simulations have also been performed to examine the structure of the Milky Way, by comparing l - v maps of simulations with those observed (Wada, 1994, Fux, 1999, Englmaier & Gerhard, 1999, Rodriguez-Fernandez & Combes, 2008, Baba et al., 2010, Dobbs & Burkert, 2012, Pettitt et al., 2014). Dobbs & Burkert (2012) showed that the nearest spiral arm, in their instance from adopting a symmetric m = 2 spiral, likely corresponds to the 'molecular ring'. However generally it is difficult to reproduce the outer Milky Way with logarithmic spirals (Englmaier & Gerhard, 1999, Pettitt et al., 2014). Fitting the l - v map from a simulation of a bar and dynamic spiral arms appears more successful (Baba et al., 2010). Baba et al. (2009) also analysed the velocities of gas and young stars from N-body+hydrodynamical simulations, and concluded that the high peculiar (non-circular) velocities they obtain, in general agreement with those observed in the Galaxy, arise from dynamic rather than stationary spiral arms.
Generally, the spiral pattern remains uncertain for the Milky Way, particularly as little is known about the spiral structure on the other side of the Galactic Center. There is also no conclusive observational evidence yet on the nature of the dynamics of the spiral arms. The Very Long Baseline Interferometer (VLBI) astrometry (e.g., VERA; Honma, 2013), as well as future space missions for infrared astrometry GAIA (Perryman et al., 2001) and JASMINE (Gouda, 2012), may well be able to provide a better indication of the nature of the spiral structure of our Galaxy.
4.7. Spiral arm triggering of star formation
A related question to the inducement of spiral arms in galaxies is whether the spiral arms induce star formation. This possibility has been considered in the quasi-stationary density wave picture, where the spiral arms induce a shock in the gas, thus raising the gas to the densities where it becomes molecular and self gravitating (Fujimoto, 1968, Roberts, 1969). In this scenario, the star formation is significantly higher with the presence of spiral shocks than it would be in a galaxy with no, or weak spiral arms. Some evidence in support of spiral arm triggering is observations by Seigar & James (2002), that show a correlation between arm strength and star formation. However other work suggests there is no difference in the star formation rate between grand design and flocculent galaxies (Elmegreen & Elmegreen, 1986, Stark et al., 1987, Foyle et al., 2011, Eden et al., 2012). Instead, the spiral arms are supposed merely to gather gas which would anyway form stars, into the spiral arms (Vogel et al., 1988), with the increase in gas densities and star formation in the arms offset by lower values in the inter arm regions. Numerical simulations support this picture (Dobbs et al., 2011), finding only a factor of ∼ 2 increase with spiral arms compared to without. The act of the spiral arms simply gathering up gas is also consistent with the picture of shocks being highly dynamic, and intermittent, as described in Section 3.5.2. However there is a tendency to form more massive clouds, and more stable clouds in the spiral arms, which may well lead to higher star formation rates in stronger spiral arms (Dobbs et al., 2011).