7. IMPACT ON COSMOLOGY

The most widely employed method that uses weak lensing data to infer information on cosmological parameters is to calculate the two-point statistics of the observed ellipticity field. As shown in Section 2.2, the intrinsic alignment of galaxies leads to additional terms being present in the observed correlation function, or power spectrum. In this section we discuss the impact of intrinsic galaxy alignments on cosmological inference and ways to mitigate it. When calculating the likelihood of cosmological parameters given a statistic, a model is required and a loss function is typically constructed that involves the observed data D and the model of that data M(π) which is dependent on some parameters of interest π, such as a set of cosmological parameters. In the case that the data is Gaussian distributed this loss function is simply

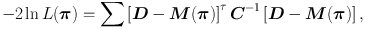(24)

where the sum is over the data points, and C is the observed covariance matrix of the data. This is the case in which the parameter dependence is in the mean of the data vector. If the model that is used to describe the data is complete, in the sense that all physical effects that can occur in the data are captured in the model, then the maximum likelihood of the inferred parameters will be unbiased. We do not have a complete model for galaxy alignments, and in this case the maximum likelihood values of the inferred cosmological parameters can be biased. In addition, any extra set of parameters φ that extend the set of inferred parameters to {π, φ} will increase the parameter-space volume and thereby increase the error bars on the parameters of interest, with respect to the case where no additional parameters were required. Such additional parameters are referred to as ‘nuisance parameters'. We show this diagrammatically in Figure 13.

Figure 13. Diagram illustrating the influence of systematic effects on cosmological parameter inference. The various ellipses represent the confidence regions for two cosmological parameters A and B, marginalised over some large multi-parameter space. In the case that no systematic effects were present, the parameters could be measured in an unbiased way (black ellipse). If there is a systematic effect and it is either ignored or incorrectly modelled, the constraints are biased by an amount and direction that depends on how incorrect the modelling is (blue ellipse). In the case that the modelling of the systematic effect is correct, the parameter errors are increased because of the larger parameter space but the result is unbiased (green ellipse); this would also be the case if nulling was applied, or a non-parametric marginalisation. If the extra systematic effects are also dependent on the parameters of interest, a strong prior on the additional parameters can even cause the original error bars to be reduced (red ellipse).

It was first shown, within the context of predicting cosmological parameter performance, that incorrect modelling can bias cosmological parameter inference in Kim et al. (2004) who showed that cosmological inference using Type Ia supernovae can be biased when systematic effects are poorly modelled. This was re-derived and applied to the case of measurement of the matter power spectrum in Huterer & Takada, (2005), and applied to the case of weak lensing systematics in Huterer et al., (2006) and Taylor et al., (2007); the approach was subsequently re-derived in Amara & Réfrégier, (2008). The fact that intrinsic alignment modelling can bias the maximum likelihood in cosmological parameter estimation was first measured and inferred empirically in Hirata et al., (2007), and first shown analytically and in a predictive sense in Kitching et al., (2008), who used a simple two-parameter model from Heymans & Heavens, (2003) to show that, in the case that intrinsic alignments were not modelled (and that the Heymans & Heavens 2003 model was correct), parameters could be biased by several percent. However such a bias was implicit in the conclusions of several earlier papers such as Heavens et al., (2000) and Hirata & Seljak, (2004), who found that intrinsic alignments could suppress the power spectrum by large amounts. There have been several elaborations that have used increasingly sophisticated and realistic models, for example Joachimi & Bridle, (2010), Kirk et al., (2010), and Kirk et al., (2012).

Figure 14 shows the ranges of possible biases on key cosmological parameters for a tomographic weak lensing survey design similar to Euclid (Laureijs et al., 2011), which are derived from a three-parameter intrinsic alignment model (representing the overall amplitude of the correlations, as well as the indices of two power-laws encoding a redshift and luminosity dependence) constrained by a collection of recent observations of early-type galaxy samples in SDSS (see Joachimi et al., 2011). The extent of the regime of possible biases beyond the credible regions of the weak lensing constraints demonstrates that ignoring intrinsic alignments would lead to significant misestimates of dark matter and dark energy parameters, while the size of the regions of possible biases, which is substantially larger than the corresponding credible regions, indicates that marginalising over this intrinsic alignment model would significantly weaken the cosmological parameter constraints. Note that we have optimistically assumed that blue galaxies do not have intrinsic alignment and, more importantly, that there is zero uncertainty on this statement. In reality, quite the opposite holds true: constraints on the intrinsic alignment signal of disc galaxies at typical redshifts and luminosities for weak lensing surveys are very poor; see Section 6.3. It is likewise optimistic to assume that early-type intrinsic alignments will be exhaustively described by just these three parameters for all relevant redshifts, luminosities, and spatial scales.

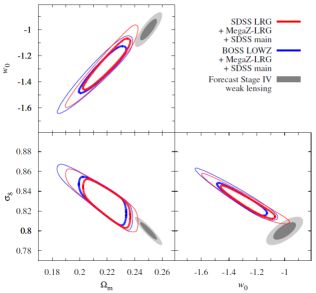Figure 14. Bias on cosmological parameters due to unmitigated intrinsic galaxy alignments for a next-generation (Stage IV, Euclid-like) weak lensing survey. A six-parameter flat ΛCDM cosmology was considered, with marginal constraints on the matter density parameter, Ωm, the normalisation of density fluctuations, σ8, and the dark energy equation of state parameter, w0. Contour lines encompass the regions in which 99% of the possible biases on these parameters are located when we sample from the 1σ credible region (thick lines) and the 2σ credible region (thin lines) of the three parameters in the intrinsic alignment model constrained in Joachimi et al., (2011). The set of red contours is obtained for the posterior of the combined samples (6 SDSS LRG samples, 2 MegaZ-LRG samples, and 2 SDSS main survey samples) analysed in Joachimi et al., (2011), while for the blue set the SDSS LRG samples have been replaced by four subsamples of the BOSS LOWZ measurements presented in Singh et al., (2014), split according to luminosity. The grey regions correspond to Fisher matrix forecasts of 1σ and 2σ constraints from a tomographic cosmic shear analysis. For details of the modelling see Joachimi et al., (2011). Note in particular that it was optimistically assumed that blue galaxies have zero intrinsic alignments, and that this is known with zero uncertainty.

It is clear that adding additional parameters to model intrinsic alignments can increase the error bars on cosmological parameters. This was first shown empirically by Hirata et al., (2007), and in a predictive capacity by Bridle & King (2007) who demonstrated that the dark energy figure of merit (Albrecht et al., 2006) could be affected by several tens of percent. Subsequent papers cited in the previous paragraph showed similar potential increases cosmological parameter error bars, however the exact predictions of each depend on the details of modelling assumed.

The majority of the bias in cosmological parameter inference is expected to be caused by incorrect modelling of the GI correlation. The II signal is generated by galaxy pairs which have physically interacted with the same matter structures. Therefore the II correlation is expected to quickly decrease in amplitude once galaxies are separated by several megaparsecs, which is readily achieved by cross-correlating galaxy samples with disjoint redshift distributions (King & Schneider 2003). Well-separated galaxy samples will still yield a GG signal as they share the gravitational shear exerted by the matter between the observer and the foreground sample. From a more formal perspective, consider the kernels in the line-of-sight projections of the GG, GI, and II signals, Equation (5) and Equation (10). Lensing efficiencies, as given by Equation (7), are smooth functions of redshift, non-zero between z = 0 and the source redshifts, whereas the intrinsic alignment signals are local effects with the redshift distribution as a kernel, which can be quite compact if adequate redshift information is available. This is illustrated in Figure 15 which shows the redshift scaling of tomographic lensing and intrinsic alignment power spectra, keeping the foregound redshift bin fixed. The GG signal displays a slow increase with redshift while the II signal quickly drops with increasing separation of the redshift distributions of the galaxy samples correlated. It is also clear from the figure that removing the GI term is more challenging: this term contains one lensing efficiency in its kernel and thus has a redshift scaling that is slightly steeper but otherwise very similar to the lensing signal.

Figure 15. Redshift scaling of the lensing and intrinsic alignment power spectra. Shown is the amplitude of the tomographic GG, II, and the negative of the GI power spectra at ℓ = 1000 as a function of the mean redshift of the background bin. The amplitude is normalised to the autocorrelation in a bin centred on z = 0.15. The photometric redshift scatter was assumed to be Gaussian with a width of 0.05(1 + z), without bias or outliers due to catastrophic failures. Note the very similar scalings of the GG and GI signals.

Instead of modelling the intrinsic alignment signal, the data vector itself can be changed to remove any contaminating signal. In reference to Equation (24) this is the act of modifying D, as opposed to M. This technique is known as ‘nulling', and takes combinations of data points that have small or zero contamination from the intrinsic alignment signal; in practice this amounts to taking linear combinations of the data points in an analogous way to principal component analysis. This approach was first suggested for weak lensing, in the context of removing small-scale information, by Huterer & White (2005). For intrinsic alignments this was revived by Joachimi & Schneider (2008) and Joachimi & Schneider (2009), relying on accurate and moderately precise redshift estimates to separate the cosmic shear and intrinsic alignment signals via the different scaling with redshift as shown in Figure 15. When nulling the intrinsic alignment signal from the data vector, information is necessarily removed (in the principal component analysis this is equivalent to ignoring, or removing, these contaminated modes) and as a result the constraints on the parameters of interest again have larger error bars, although the maximum likelihood should be unbiased if the remaining part of the data vector can be modelled well. An analogous null test can be constructed from decomposing the shear field into a divergence-free (B-mode) and a curl-free (E-mode) part. To very good approximation, lensing only generates E-modes (Hilbert et al., 2009), so that a B-mode correlation signal would indicate the presence of systematic effects. Intrinsic alignment models predict significant B-modes (Giahi-Saravani & Schäfer, 2014) although measurements from mock catalogues suggest these are also negligible (Joachimi et al., 2013b).

The final approach that can be taken, in reference to Equation (24), is to modify the covariance matrix C, effectively increasing the error bars to account for a marginalisation over non-parameter functional behaviour that cannot be modelled. This ‘path integral' approach was derived by Kitching & Taylor (2011) (and a similar non-parametric approach taken in Kitching et al., 2009) and applied to intrinsic alignments. The authors found that the scale and redshift dependence of the functional form of the intrinsic alignment signal needs to be known to better than 10 % for the cosmological error bars to be unaffected.

It is possible to include additional data in the likelihood analysis, which, due to a different sensitivity to weak lensing and intrinsic alignment signals, calibrates the nuisance signal internally. Weak lensing catalogues also contain galaxy positions, so that clustering signals and cross-correlations between galaxy position and galaxy ellipticity (which on small scales corresponds to galaxy-galaxy lensing) can be added to D without the need for extra data. This was first proposed by Bernstein (2009) and shown by Joachimi & Bridle (2010) to self-calibrate flexible models of intrinsic alignments with minimal assumptions such that cosmological parameter constraints are not degraded by more than factors of a few compared to pure weak lensing analysis without intrinsic alignments or extra data. Sub-dividing the data into tomographic redshift bins is crucial for this purpose, and the self-calibration performance may be further improved by a split between blue and red galaxies which are known to have largely different intrinsic alignment signals (see Section 6). The combination of galaxy weak lensing with lensing statistics derived from the cosmic microwave background (CMB), which are not affected by intrinsic alignment effects (note that a cross-correlation between galaxy samples and CMB lensing would be affected by a GI term), also seems a promising route (Kitching et al., 2014a). See Kirk et al., (2015) for a more quantitative comparison of some intrinsic alignment mitigation techniques.

In principle there is also cosmological parameter information in the intrinsic alignment signals, e.g. in the distance ratios that govern the redshift scaling of the signals (Kitching & Taylor 2011, Chisari & Dvorkin 2013). However, it is currently unclear if the sensitivity to cosmology will ever outweigh the statistical errors and the uncertainty in the models. Intrinsic alignments also effect the three-point statistics of the ellipticity field, analogously to their impact on two-point statistics. Semboloni et al. (2008) found stronger contamination for three-point statistics in simulated data than at the two-point level, which could be exploited to self-calibrate intrinsic alignments by combining these statistics. However the modelling is commensurately more difficult at the three-point level. Maps of weak lensing convergence have been proposed as a starting point to extract more advanced statistics of the shear pattern on the sky. The impact of intrinsic alignments on the map-making process and the derived statistics clearly warrants further investigation (see Fan 2007 for an early investigation into the impact of intrinsic alignments on peak counts in such maps). Moreover, if one attempts to measure lensing using galaxies in the background, but has imperfect redshift information and thus contamination from galaxies at the same redshift as the lens, then intrinsic alignments can also contaminate galaxy-galaxy lensing (Blazek et al., 2012) and need to be mitigated, perhaps using forward modelling approaches analogous to those used for cosmic shear.

Because the intrinsic alignment of galaxies with matter densities is a local effect, photometric surveys that infer the distance information of galaxies using broad-band colours do not provide a sufficiently precise measurement, and as a result the intrinsic alignment and lensing signals are mixed up in the ellipticity measurements. Hence, to provide calibration information that yields priors on parameters of an intrinsic alignment model at the likelihood stage, data with precise redshift information is required. In the following section we will return to the question of what kind of survey will be able to provide this critically important extra information for the galaxy samples observed with forthcoming weak lensing surveys.