


Rather than studying galaxy alignments in particular environments, as done in the previous sections, one can alternatively analyse spatial correlations involving galaxy ellipticities or position angles in more generally selected, usually large, galaxy samples, and the matter density contrast as traced by (the same or different) galaxies. While the interpretation of the resulting signals in terms of galaxy evolution processes may be more involved in this case, these measurements are closely linked to the intrinsic alignment contamination of weak lensing statistics and benefit from the rigorous measurement and analysis techniques developed for galaxy clustering and cosmic shear.
In the standard picture of galaxy formation, the large-scale structure interacts with the forming galaxy through accretion and by exerting tidal torques (Section 2.3) and therefore determines the boundary conditions for the luminous components inside the dark matter host halo. Primarily, there are six models for explaining galaxy alignments, which differ substantially in their physical picture (see Table 2 for a summary):
The simplest model of alignment is the alignment of the stellar component with the dark matter host halo structure due to identical dynamical properties, for example identical velocity tensors of both components due to equilibration. These halo shape models are thought likely to apply to elliptical galaxies.
Tidal shear alignment models, dubbed linear alignments, assume that elliptical galaxies are embedded in the gravitational tidal field generated by the ambient cosmic large-scale structure (at least over some period in the galaxys history) and that the galaxy halo ellipsoid is tidally distorted. The stellar distribution then follows this distortion (see Section 2.3).
Perhaps the best-studied intrinsic alignment models with the clearest physical picture are angular momentum alignments: here, the host halo builds up angular momentum by the tidal shearing mechanism and one assumes that the galactic disc's symmetry axis is aligned with the angular momentum of the host halo. Due to the fact that angular momentum generation is a perturbative effect, these particular alignments are already present in the initial conditions of structure formation. Dubbed quadratic alignment models because of their dependence on the gravitational potential, these angular momentum alignments are thought to govern the shape alignment of spiral galaxies (see Section 2.3).
Vorticity alignments have recently attracted much interest, as strong alignments between dark matter haloes and the large-scale vorticity field were found in simulations. In contrast to the models discussed above, vorticity generation (and possibly alignment as well) is a purely non-linear effect.
Accretion models stipulate that the shape and orientation of the stellar component is related to the pattern of accretion of matter onto the galaxy. Like vorticity alignments, accretion alignments would require an understanding of non-linear structure formation for predicting the accretion pattern e.g. in terms of its multipolarity.
Closely related to the preceding case are merging models which consider the infall of galaxies rather than of raw gas and dark matter. Assuming that angular momentum defines the orientation of the system, as applicable to spiral galaxies, the angular momentum of the system results from the conversion of the orbital angular momenta of progenitor galaxies or haloes in merging processes.
A common feature of these models, further discussed in Section 6.4, is the notion that galaxy alignment is a local process, i.e. alignments of the stellar component with any surrounding field are determined by the interaction of the galaxy with that field, meaning that neighbouring galaxies do not interact directly with each other, but may have coherent alignments due to their interaction with the same large-scale density field.
| model | field | mechanism | galaxy type |
| halo shape | halo inertia | identical velocity tensor of baryons and dark matter | ellipticals |
| linear alignment | tidal shear | tidal field acts on stellar component | ellipticals |
| quadratic alignment | angular momentum | stellar disc reflects angular momentum | spirals |
| vorticity | vorticity direction | halo alignment due to non-linear dynamics | unknown |
| accretion | accretion pattern | accretion pattern determines ellipticity | unknown |
| merging | angular momentum | conversion of orbital momentum to spin | spirals |
Our discussion below is divided into descriptions of generally large-scale alignments for different galaxy types for which there are different physical mechanisms that are believed to cause the alignments. Observations of such alignments are critical for understanding the amplitude of, and mechanism behind, intrinsic alignments on the scales that will be used for cosmological weak lensing measurements. At the same time, these are challenging measurements to carry out because they require a large contiguous area (to find many galaxy pairs with large separations) that has high enough imaging quality that galaxy shapes or spins can be robustly estimated, as well as either spectroscopic redshifts or high-quality photometric redshifts. While a large contiguous area is necessary, the sampling rate (number density of usable galaxies) also cannot be too low, since that will also increase the noise. Unlike the types of observations described in Section 3, the necessary datasets for this type of observation did not exist with sufficient quality until the start of this century.
6.1. General observational studies
First we describe some general observational studies that sought to observe intrinsic alignments without making a distinction between galaxy types that might have different underlying alignment mechanics.
The first study of intrinsic alignments that had many galaxy pairs on the scales used for cosmological weak lensing analysis was that of Brown et al., (2002). They used digitized photographic data (which is subject to a number of technical difficulties in shape measurement, see Section 1) from the SuperCOSMOS Sky Survey (Hambly et al., 2001). This study took advantage of the fact that at low redshift, cosmic shear is extremely small, and hence non-zero galaxy shape correlations should be due to intrinsic alignments. Unlike later approaches to measuring large-scale intrinsic alignments, they used all galaxy shapes without any redshift information, except the general knowledge that the overall galaxy redshift distribution was at quite low redshift around z = 0.1. Using 2× 106 galaxies, they found galaxy shape correlations (corresponding to II correlations; see Section 2.3) out to separations of 100 arcmin, the maximum scale for which measurements were made.
After this finding, Heymans et al., (2004) carried out a re-analysis of the COMBO-17 survey (Wolf et al., 2001) weak lensing results (Brown et al., 2003), allowing for the possibility of some II-type intrinsic alignments contaminating the results for galaxy pairs that are nearby in redshift, taking advantage of the good photometric redshifts from COMBO-17 to reliably create samples of galaxy pairs that are close and distant along the line-of-sight. The intrinsic alignments were found to lead to at most a few percent-level effects. Some later papers used the cross-correlation between spectroscopic samples and those with potentially much poorer photometric redshifts to constrain large-scale intrinsic alignments of mixed galaxy samples (Blazek et al., 2012, Chisari et al., 2014), thus far producing only upper limits due to their focus on faint, mixed-type galaxy samples.
Early-type galaxies are thought to align themselves with the large-scale structure through the linear alignment model (Hirata & Seljak 2004); see Section 2.3. If there is dynamical equilibration between the dark matter and the stellar components, one can expect that the shape of the luminous component reflects the shape of the dark matter halo. If the halo is now embedded into the large-scale structure, gravitational tidal fields will distort the potential of the halo and the luminous component rearranges itself while maintaining virial equilibrium as long as the gravitational shear is not strong enough to disrupt the halo (Camelio & Lombardi 2015). For sufficiently small tidal shears one can expect a linear relationship between the observed (projected) shape and the strength of the tidal fields. In addition, this linear relationship is the simplest one allowed by symmetry as the tensor of second moments of the stellar brightness distribution is a symmetric tensor of rank two, just like the tidal shear tensor. Typically, there is a single parameter involved which characterises the proportionality between ellipticity and tidal shear. Alignments of this type are correlated on scales on which the tidal shear is correlated, which is identical to the correlation length of the density field. This straightforward picture of alignments for elliptical galaxies would be challenged if the stellar component contains a (velocity) structure on its own or if this could not be directly related to the host halo properties, for instance due to a strong anisotropy of the stellar velocity dispersion. Likewise, incomplete virialisation or remnants from previous merging processes would add further complication.
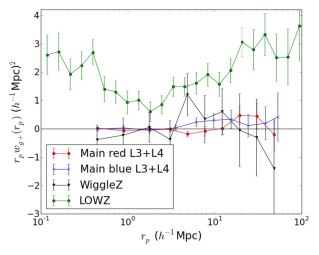
Observational constraints on intrinsic alignments of red galaxies come from studies starting in 2006 or later. These studies focused on samples with both redshifts and shear estimates for each galaxy, and took advantage of the density-shape correlation measured via Equation (16), which for typical intrinsic alignment models can be measured at higher signal-to-noise than shape-shape correlations (and are a more important contaminant to cosmic shear via the GI term, as well; see Section 7). The SDSS has emerged as the leading survey for these studies, with highly significant measurements of density-shape alignments out as far as 100 Mpc / h for red galaxy samples, and upper limits for blue galaxy types. The analyses have been carried out by several groups (Mandelbaum et al., 2006b, Hirata et al., 2007, Paz et al., 2008, Okumura et al., 2009, Joachimi et al., 2011, Lee 2011, Li et al., 2013, Singh et al., 2014), including in Joachimi et al., (2011) the development of a formalism to use high-quality photometric redshifts, and model out the contamination from galaxy-galaxy lensing due to incorrectly identified galaxy pairs (see also Blazek et al., 2012). The highest redshift measurements with SDSS for red galaxies extend to z ∼ 0.6, by Joachimi et al., (2011) and Li et al., (2013). These works employed two different statistical measures of the alignments, the former using shapes and the latter using position angles alone, and they both had a clear detection to tens of megaparsec scales.
An illustration of the measurements that led to the aforementioned conclusions about large-scale intrinsic alignments of early-type galaxies is shown in the left panel of Figure 12. For early-type galaxies, the amplitude of the intrinsic alignment signal has been found to scale roughly linearly with the galaxy luminosity (Joachimi et al., 2011, Singh et al., 2014). The right panel of Figure 12 shows that both hydrodynamic simulations (Tenneti et al., 2015) and analytic models, based on Equation (16), are able to describe the scaling of red galaxy intrinsic alignments with transverse separation. The curve from hydrodynamic simulations is a prediction, while the curve from an analytic non-linear extension of the linear alignment model (for details see Kiessling et al., 2015) is a fit to a functional form with a free amplitude.
 |
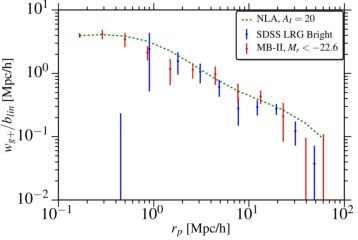 |
Figure 12. Left: Examples of some large-scale intrinsic alignments measurements in the literature, employing a galaxy position-shape correlation function, wg+, as a function of comoving transverse separation between galaxies, rp. The samples called “Main” refer to the SDSS main (flux-limited) spectroscopic sample, divided into two subsamples, both at intermediate (Milky Way-type) luminosities. The red sample results use the sample from Hirata et al., (2007), but were re-measured by Joachimi et al., (2011) using a different colour cut that is more consistent with ones used by later works. The WiggleZ results come from Mandelbaum et al., (2011), and the LOWZ (a low-redshift sample from the SDSS BOSS survey) results come from Singh et al., (2014). Right: A comparison of the observed density-shape correlation for LRGs in SDSS, a prediction from the MassiveBlack-II (MB-II) hydrodynamic simulation, and the non-linear alignment model. As shown, both hydrodynamic simulations and this simple analytic model are well able to reproduce the scaling of the observed density-shape correlations with separation. The data and predictions have been normalised by the linear galaxy bias, here referred to as blin, relating the galaxy and matter overdensities, δg = blinδ. The analytic model labelled 'NLA' corresponds to a slightly modified version of Equation (16); see also Bridle & King (2007). Right-hand figure based on data from Tenneti et al., (2015), with credit to Sukhdeep Singh. |
|
The alignment of late-type galaxies follows an equally persuasive physical picture, but there are two competing mechanisms as possible explanations. Late-type spiral galaxies have formed a galactic disc which, depending on the angle of inclination, is perceived to have a certain ellipticity. The inclination of the disc must be determined by its angular momentum, but how the angular momentum is ultimately linked to the surrounding large-scale structure is not as clear. It is worth emphasising that the ellipticity in these models, being an orientation effect, depends only on the angular momentum direction.
A widely employed picture of angular momentum generation is tidal torquing (Section 2.3), where the gravitational field of the large-scale structure exerts a torquing moment on the protohalo prior to collapse. When, at a later stage, a galactic disc is formed through the cooling of the baryonic component followed by star formation, the galactic disc can be expected to follow the host halo angular momentum imprinted by tidal torquing (Crittenden et al., 2001, 2002). Employing this picture for predicting intrinsic alignments requires a model for the dynamics of dark matter in tidal shearing and the possibly strong assumption that there are no misalignments between the disc symmetry axis and the host halo angular momentum. An environment dependence would be introduced by the typical tidal field strength and the typical orientation of the tidal shear tensor. Based on tidal torquing one can expect relatively short-ranged correlations of not much more than 1 Mpc (Schäfer & Merkel 2012). Although tidal torquing has been tested as a source of angular momentum of dark matter haloes (Porciani et al., 2002a, 2002b), there are alternatives such as the conversion of orbital angular momentum to spin, as suggested by Codis et al., (2012); Dubois et al., (2014), which would yield similar correlation functions, but with a strong environmental dependence.
Clearly, tidal torquing would be challenged if merging of subhaloes is important, as each merging process adds new angular momentum to the halo. In this model, the angular momentum direction and ultimately the disc orientation would fluctuate strongly between merging events in contrast to the steady orientation in the tidal torquing picture. There might be scenarios, however, where the merging takes place along preferred directions, which would stabilise the angular momentum direction. These effects can be important in sheets and filaments. Whereas in the first case there would be little correlation between haloes, the second case would suggest relatively long-ranged correlations, typically of the size of filaments. Tidal torquing must have a straightforward parameterisation describing the orientation of angular momentum as a function of tidal shear. As merging of subhaloes can be expected to take place along directions defined by the orientation of the tidal shear tensor, there is in fact a similar parameterisation applicable to these cases.
For rotationally-supported galaxies there are clearly two direction vectors of interest, one defined by the angular momentum and the other defined by the projected galaxy shape. Observational studies have considered alignments of both of these vectors. Lee & Pen (2002), Lee & Erdogdu (2007), and Lee (2011) approached this question observationally using the direction of the disc angular momentum for nearby galaxies. Lee & Pen (2002) correlated the spin direction of disc galaxies (determined based on axis ratios and position angles, assuming disc galaxies are infinitely thin with spin axis perpendicular to the disc) with the local tidal shear field reconstructed from the IRAS PSCz survey. They detected a correlation at more than 3σ confidence consistent with the linear tidal-torque model. Lee & Erdogdu (2007) later carried out a similar analysis, but using the 2MASS Redshift Survey to reconstruct the tidal field and ∼ 12k galaxies from the Tully Galaxy Catalog. They again found a highly significant (6σ) detection of correlation between the spin direction and the intermediate principal axis of the tidal field, which was found to be stronger in high-density regions than in low-density regions. Finally, Lee (2011) used data from SDSS to measure the spatial correlation function of the 3D spin directions of pairs of nearby (z ≤ 0.02) disc galaxies, finding a ∼ 3σ detection around separations of 1 Mpc / h and no detection for scales above 3 Mpc / h.
On the other hand, attempts to measure large-scale intrinsic alignments of the projected shapes of late-type galaxies in Hirata et al., (2007) led only to upper limits on the effect for the SDSS Main galaxy sample at z ∼ 0.1. The later emergence of additional spectroscopic surveys that targeted somewhat deeper or differently-selected galaxy samples in the SDSS region also proved useful, as it allowed for additional measurements beyond those enabled by SDSS spectroscopy alone. Examples of such surveys include the WiggleZ survey (Drinkwater et al., 2010), which was used by Mandelbaum et al., (2011) to constrain the intrinsic alignments of a very blue starburst galaxy population at intermediate redshifts, z ∼ 0.6. Again, only upper limits were placed in this case (see Figure 12). It is worth commenting on the possible explanations for the detections of spin correlations for ≲ 1 Mpc / h scales for nearby disc galaxies by Lee, (2011), versus non-detections of shape correlations by Hirata et al., (2007) and Mandelbaum et al., (2011). First, it is important to bear in mind that the large-scale studies of shape correlations have little statistical power on ≲ 1 Mpc / h scales, making it hard to compare them with the results for spin alignments on those scales. Second, projection along the line-of-sight separations out to tens of Mpc to make 2D correlation functions can wash out 3D correlations that are present at scales of ≲ 1 Mpc / h, making them entirely undetectable. Finally, it has been shown (e.g., Heymans et al., 2006a) that putting in models for disc angular momentum with the local density field can result in quite small projected shape correlations. Given these three caveats, it is not clear that there is any discrepancy at all between the measurements using spin and shape alignments.
6.4. Alternative alignment mechanisms
In contrast to the specific alignment models for early- and late-type galaxies discussed above, there are a number of alternative hypotheses on how dark matter haloes, irrespective of the type of the galaxy they contain, can be aligned with the large-scale structure. It is important to emphasise that these are conceptually new, and use a different aligning large-scale field other than the tidal shear as is the case for the linear and quadratic alignment models.
One such model posits that the stellar component of a galaxy would simply follow the halo shape, as would be expected from virial equilibrium, very much like in the case of elliptical galaxies. The individual galaxies would appear correlated through correlations in the dark matter halo shapes and orientations, which are already present in the initial conditions of structure formation and can in principle be determined as an extension to the random process that seeds haloes into the large-scale structure as peaks in the density field (Bardeen et al., 1986, Bond et al., 1996, Schneider et al., 2012, Rossi 2012, Angrick 2014). In this picture, halo shapes are related to the curvature of the density field, which would imply short ranged correlations.
Secondly, alignments of dark matter haloes with the local vorticity field have been observed in numerical simulations (Libeskind et al., 2012, 2013). The actual mechanism is, in contrast to tidal torquing, difficult to grasp via perturbation theory or other analytic means because vorticity generation only occurs in non-linear structure formation. If the stellar component follows the orientation of the dark matter halo, one would observe a shape correlation which would be induced by correlations in the vorticity field, which is expected to show correlations only on small scales.
Thirdly, accretion of matter can determine shape and orientation of the stellar component. Numerical simulations of individual (spiral) galaxies have shown the presence of cold gas accretion streams (Dekel et al., 2009, Keres et al., 2009, Sales et al., 2012), which have a significant impact on the orientation of the disc and are able to tilt the orientation away from the initial one (Kimm et al., 2011, Danovich et al., 2012, Danovich et al., 2014), up to the point where the angular momentum direction shows a random walk behaviour at successive merging events (Dubois et al., 2014). It is difficult to make a statement about shape correlations which would arise in such a model, but it seems reasonable to assume that such correlations would strongly depend on the topology of the region of large-scale structure the corresponding galaxies reside in Prieto et al., (2014).