Annu. Rev. Astron. Astrophys. 2013. 51:63-104 Copyright © 2013 by Annual Reviews. All rights reserved

2. THE THREE-DIMENSIONAL DUST RADIATIVE TRANSFER PROBLEM

2.1. The Radiative Transfer Equation

The stationary radiation field is described by the specific intensity I(x, n, λ), where x is the location in space, n is a unit vector indicating the direction of the radiation, and λ is its wavelength. The specific intensity represents the amount of energy carried by radiation in a unit wavelength interval, which is transported per unit solid angle and per unit time across an element of unit area perpendicular to n. (The specific intensity can be defined as the intensity per unit of wavelength or per unit of frequency. The typical convention is to indicate it with a subscript, i.e., as I_λ or I_ν. We adopt the per unit of wavelength convention and drop the subscript so as not to overload the notations.) The continuum RTE describes how the specific intensity varies as a result of interactions with a medium filled with sources and sinks. In its general form, it can be written as (see e.g., Chandrasekhar 1960, Rybicki & Lightman 1979)

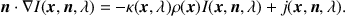(1)

The left-hand side of this equation represents the change in intensity over an infinitesimal distance along the path determined by the position x and the propagation direction n. The first term on the right-hand side represents the extinction, i.e., the loss of radiant energy, when radiation passes through matter. Here, κ(x, λ) is the mass extinction coefficient, and ρ(x) is the mass density. The second term on the right-hand side represents the source term, i.e., the new luminosity released into the medium at x in direction n. The complexity of the RTE depends on the nature of the source and sink terms, i.e., the different physical processes that are responsible for extinction and emission.

An alternative form of the RTE (Equation 1) uses explicitly the distance s along the path defined by a position x and propagation direction n as a variable. We then obtain

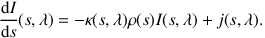(2)

If we assume for now that the source term j does not depend on the intensity I, we can readily solve the differential equation

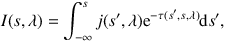(3)

with the optical depth between two positions defined as

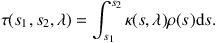(4)

Equation 3 has a simple physical interpretation: It shows that the intensity at any position s along a path results from the emission at all anterior points s' along the path, reduced by a factor of e^{?τ(s, s', λ)} to account for the extinction from the intervening matter. We stress that Equation 3 is only a formal solution of the RTE but not a very useful one. Indeed, the emissivity generally does not only depend on position, direction, and wavelength, but also on the specific intensity itself. The formal solution (Equation 3) is then no more than an integral equation of the RTE itself; this is particularly the case for dust RT. The remainder of Section 2 gradually expands the dust RTE by including the various relevant physical processes.

2.2. Primary Emission and Absorption

Primary emission and absorption in a dusty medium are two important and obvious processes to take into account. Primary emission accounts for the radiative energy added to the radiation field– this is often stellar emission, but it can also include, for example, radiation from an AGN, emission line radiation from ionized gas, or Bremsstrahlung. In general form, it can be characterized by a function j_*(x, n, λ). Absorption is the process in which electromagnetic radiation is taken up by dust grains and transformed into the internal energy. It is characterized by the absorption coefficient κ_abs; for a given chemical composition, size, and shape of a dust grain, the absorption coefficient can in principle be determined at any wavelength (Mie 1908, Purcell & Pennypacker 1973, Draine 1988, Mishchenko, Travis & Lacis 2002, Min, Hovenier & de Koter 2005).

When we take only primary emission and absorption by dust into account, the RTE (Equation 1) becomes

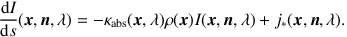(5)

This equation is a simple first-order differential equation, which can be solved by simply integrating along the line of sight, as is done for the formal solution (Equation 3). For general 3D geometries, this integration is done numerically.

2.3. Including Scattering

The complexity of the RTE increases substantially when we take scattering into account. Scattering, as with absorption, removes radiation from a beam and hence accounts for a second sink term in the RTE, the efficiency of which is quantified by the scattering coefficient κ_sca. Rather than converting the radiation to internal energy, it emits the same radiation in a different direction. Scattering therefore does not only imply a second sink term, but also a second source term. The scattering phase function Φ(n, n', x, λ) describes the probability that a photon originally propagating in direction n' and scattered at position x, will have n as its new propagation direction after the scattering event. Given this definition, the phase function satisfies the normalization

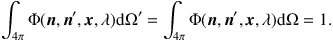(6)

Adding to the RTE the sink and source terms due to scattering, we obtain

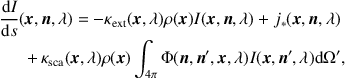(7)

where the extinction coefficient κ_ext = κ_abs + κ_sca. Unlike the simple differential equation (Equation 5), Equation 7 is an integro-differential equation in which the radiation fields at all different positions and in all different directions are coupled.

In many RT calculations, scattering is important and adds significant complexity, given that dust scattering is anisotropic. This is especially true for UV to NIR wavelengths: Observations indicate that the dust scattering albedo at these wavelengths is at least 50% and that scattering off dust grains is strongly anisotropic (Mattila 1970, Calzetti et al. 1995, Burgh, McCandliss & Feldman 2002, Gordon 2004). [http://www.stsci.edu/~kgordon/Dust/Scat_Param/scat_data.html contains the up-to-date versions of the original plots of albedo and scattering phase function asymmetry versus wavelength from Gordon 2004.] Using an isotropic phase function or other approximations such as an isotropic two-stream approximation or a (effective) forward scattering (see e.g., Code 1973, Natta & Panagia 1984, Calzetti, Kinney & Storchi-Bergmann 1994) might not always be physically justifiable. Several authors demonstrated that improper treatment of anisotropic scattering leads to significant errors (e.g. Bruzual, Magris & Calvet 1988, Witt, Thronson & Capuano 1992, Baes & Dejonghe 2001). Even for radiation at mid-infrared (MIR) wavelengths or longer, where the scattering off common ISM grains is low, an application calculating the heating of the grains will need to properly handle the scattering (Nielbock et al. 2012).

The Henyey-Greenstein (HG) phase function (Henyey & Greenstein 1941) is the most widely used parametrization of the dust phase function and provides a good single-parameter approximation. Dust grain models predict small deviations from an HG phase function, and other parametrizations or numerical phase functions can be used for increased accuracy (Kattawar 1975, Hong 1985, Draine 2003b).

2.4. Radiative Transfer in Dust Mixtures

In any real dust medium, there is a range of different types of dust grains present, with various chemical compositions, sizes, shapes, and number densities. Each grain type i is characterized by its own absorption coefficient κ_abs,i(λ), scattering coefficient κ_sca,i(λ), and scattering phase function Φ_i(n, n', λ). If we denote the relative contribution of each grain type i at the position x to the total dust number density as w_i(x), the RTE becomes

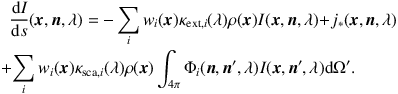(8)

Clearly, Equation 8 is formally identical to Equation 7, if we define the absorption coefficient, scattering coefficient, extinction coefficient, and scattering phase function of a dust mixture as, respectively,

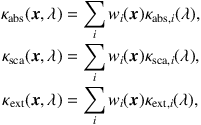(9a) (9b) (9c)

and

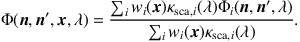(9d)

In terms of primary emission, absorption, and scattering, RT in dust mixtures is completely identical to RT in a dust medium with a single average dust grain, and no approximations are needed (Martin 1978, Wolf 2003a).

2.5. Including Dust Emission

In addition to primary emission, absorption, and scattering, a fourth physical process in dust RT, the thermal emission by the dust itself, must be taken into account. Dust grains that absorb radiation re-emit the acquired radiative energy at wavelengths longward of ~ 1 µm. To account for this astrophysical process, we need to incorporate the third source term j_d(x, λ) in our RTE:

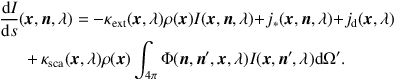(10)

The dust emissivity term could be perceived as merely an extra source term similar to the primary stellar emissivity term. Its exact form is strongly dependent on which physical emission processes are important, and often it depends, in a complicated and nonlinear way, on the intensity of the radiation field itself.

A common assumption is that the dust grains are in thermal equilibrium with the local interstellar radiation field. In this case, the emissivity of the population of grains of type i can be written as a modified blackbody emission characterized by the equilibrium temperature T_i(x). Summing over all populations, we obtain

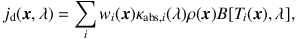(11)

where B(T, λ) is the Planck function. The equilibrium temperature of each type of grain is determined by the balance equation, i.e., the condition that the total amount of energy absorbed equals the total amount of emitted energy:

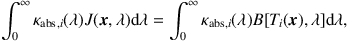(12)

where J(x, λ) represents the mean intensity of the radiation field,

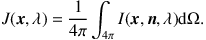(13)

The equilibrium temperature of the dust grains depends explicitly on their size and chemical composition. At the same location, dust grains of different sizes and/or chemical compositions will obtain different equilibrium temperatures. So far, we have easily combined the absorption and scattering due to different kinds/sizes of dust grains in the RTE without any approximations. The same cannot be done for the thermal re-emission term. One could compute the average temperature for the different grains on the basis of Equation 2.4 and obtain a mean temperature. This results in reducing the complexity of the dust mixture at a given position to a single mean grain that will reach a single equilibrium temperature. Although this could be useful, sufficient, or even necessary for certain applications, this is a physically incorrect simplification of the RT problem (e.g. Wolf 2003a).

Although the assumption of thermal equilibrium is useful in some applications, it breaks down in others. Particularly important is the case where the dust medium contains very small dust grains [including polycyclic aromatic hydrocarbons (PAHs)]. Large dust grains reach thermal equilibrium and emit as modified blackbodies with an equilibrium temperature. However, small dust grains have small heat capacities, and the absorption of even a single UV/optical photon can substantially heat the grain. These small grains will not reach the equilibrium temperature but will instead undergo temperature fluctuations that lead to grain emission at temperatures well in excess of the equilibrium temperature. The emission from small grains is necessary to explain the observed MIR emission of many objects (see, e.g., Sellgren 1984, Boulanger & Perault 1988, Helou et al. 2000, Smith et al. 2007, Draine et al. 2007). When including such transiently heated dust grains, the dust emissivity changes from Equation 14 to

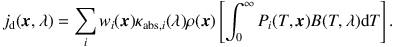(14)

Here, P_i(T, x) is the temperature distribution for dust grains of type i at the location x. This temperature distribution depends on the chemical composition and size of the dust grains, as well as on the intensity and hardness of the radiation field in which it is embedded. Several methods have been developed to calculate the temperature distribution of small dust grains, using either matrix operations or time averages (see, e.g., Dwek 1986 Desert, Boulanger & Shore 1986, Guhathakurta & Draine 1989, Siebenmorgen, Kruegel & Mathis 1992, Draine & Li 2001, Compiègne et al. 2011). The result is that the dust source term is an intricate, nonlinear function of the specific intensity, which adds significant complexity to the RT problem.

Finally, thermal emission is not the only emission process of dust grains: Additional nonthermal processes are extended red emission (Witt & Boroson 1990, Smith & Witt 2002) and blue luminescence (Vijh, Witt & Gordon 2004). These nonthermal processes can account for a substantial fraction of the surface brightness of interstellar clouds at optical wavelengths (see, e.g., Gordon, Witt & Friedmann 1998, Witt et al. 2008). Both processes can be included as an additional term in the dust source term j_d(x, λ) in Equation 10.

2.6. Radiative Transfer of Polarized Radiation

The specific intensity I(x, n, λ) is not a complete description of the radiation field, as it describes only unpolarized light. Scattering of photons from dust grains naturally produces polarized radiation (Gordon et al. 2001, figure 2). In addition, aligned dust grains also produce polarized radiation (Whitney & Wolff 2002). Although alignment of grains has been demonstrated observationally for many decades, the physical mechanism for grain alignment is still a matter of debate (Lazarian 2007).

The most common description of polarized radiation uses the Stokes vector S = (I, Q, U, V ), where I is the total specific intensity, Q and U the linearly polarized intensity in two axes rotated 45° from one another, and V the circularly polarized intensity. The four components do not form a preferred basis of this space, but were chosen because they can be easily measured or calculated.

The RT formalism we describe above can be extended to include polarized radiation. Instead of a single RTE, we then obtain a vector RTE, or equivalently, a set of four coupled scalar equations:

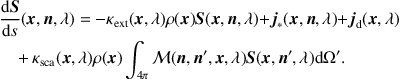(15)

The first complication is the scattering source term, where a 4×4 scattering (or Mueller) matrix (n, n'&, x,λ), which describes the changes in the Stokes vector when radiation is scattered from propagation direction n′ to a new propagation direction n, replaces the phase function Φ(n, n', x,λ). For a full description, see e.g., Bohren & Huffman (1983); Fischer, Henning & Yorke (1994); or Code & Whitney (1995). When we consider RT of polarized light through a dust mixture, each type i of grain is characterized by its own Mueller matrix _i(n, n', λ). The RTE can then still be written as Equation 15:

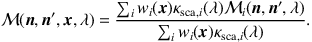(16)

A second complication is the thermal emission term: The full Stokes vector is used for thermal emission from aligned grains.