

Galaxy clusters are the largest gravitationally bound objects in the current universe. They reach total masses of ∼ 1013 − 1015 M⊙, only about ∼ 3-5% of which is in the member galaxies. The other two major components are the “intracluster medium” (ICM), a hot, ionized plasma that comprises ∼ 15-17% of a cluster’s mass, and the majority of the mass (∼ 80%) exists in the form of “dark matter” (DM), the precise nature of which is at present unknown, but is likely comprised of weakly-interacting non-baryonic particles.
The ICM is one of the largest-scale examples of a space plasma, and was discovered in early X-ray observations of clusters (e.g., Cavaliere et al. 1971, Meekins et al. 1971, Kellogg et al. 1972, Forman et al. 1972, Serlemitsos et al. 1977). It consists of fully ionized hydrogen and helium with traces of highly ionized heavy elements at roughly solar to one-third solar abundances. With electron densities of ne ∼ 10−4 − 10 − 1 cm − 3 and temperatures of T ∼ 106 − 108 K, the ICM radiates in X-rays predominantly through bremsstrahlung, 2-photon emission, photo and dielectronic recombinations, and line emission due to collisional excitation processes. Except for the brightest emission lines in the cores of clusters, the gas is optically thin to such X-rays. Inverse Compton scattering of the cosmic microwave background (CMB) off of the thermal electrons in the ICM leads to observable distortions in the CMB spectrum known as the Sunyaev-Zeldovich effect (Sunyaev & Zeldovich 1972). Observations of radio sources in clusters and Faraday rotation measurements reveal that the ICM is weakly magnetized (see Carilli & Taylor 2002, Feretti et al. 2012, for reviews), with magnetic field strengths of B ∼ 0.1 − 10 µG, corresponding to a magnetic pressure which is roughly a few percent of the thermal pressure.
Table 1 shows the relevant length scales of the ICM for typical values of the density, temperature, and magnetic field strength. First, we see that the ICM is weakly collisional, since the typical dynamical scales of interest range from ∼100-1000 kpc and the electron and ion mean free paths are on the order of less than a tenth of a kpc (as in the case of the core of the Virgo cluster) up to tens of kpc (as in cluster outskirts). Under these assumptions, the ICM is typically modeled as a collisional fluid using the equations of hydrodynamics (HD) or magnetohydrodynamics (MHD), though structure on scales below several kpc are observable and thus of interest, where, formally, the assumption of collisionality is violated. Second, the relevant scales for plasma physics (e.g., the inertial lengths and Larmor radii of the electrons and ions) are many orders of magnitude smaller than these scales, and are not directly observable. It should also be noted that though in one sense the effect of the magnetic field is “strong” due to the fact that the electron and ion Larmor radii are orders of magnitude smaller than their mean free paths, in another sense the magnetization is “weak” since over most of the cluster volume the magnetic pressure is much weaker than the thermal pressure. As we discuss below, accounting for these effects in physical models of the ICM has important and potentially observable consequences.
| Length Scale | Value |
| Debye Length | 100 fpc |
| Electron Skin Depth | 2000 fpc |
| Electron Larmor Radius | 0.05 npc |
| Ion Skin Depth | 0.08 npc |
| Ion Larmor Radius | 2 npc |
| Mean Free Path | 1 kpc |
| Cluster Core Radius | 100 kpc |
| Cluster Virial Radius | 1000 kpc |
| a Keeping the astrophysical length unit kpc as the most practical reference, we express smaller lengths in nanoparsec (npc) and femtoparsec (fpc). We assume ICM conditions of ne ∼ np = 0.01 cm − 3, kT = 5 keV, and B = 1 µG, except the last two scales, which are global. | |
The launch of the Chandra X-ray Observatory in 1999 provided a unique window into the physics of the ICM, due to its ∼0.5-arcsecond spatial resolution. However, even for deep observations of the diffuse ICM emission, realistically the resolution is reduced to a few arcseconds due to the need for sufficient photon statistics. Nevertheless, for nearby clusters at distances of 16 to 300 Mpc from us, an angular resolution of 3 arcsec still corresponds to a projected spatial resolution on the sky of about 0.25 kpc to 4 kpc, a scale comparable to the particle mean free path. Among the first cluster discoveries by Chandra were sharp edges in surface brightness, first seen in the clusters A2142 (Markevitch et al. 2000) and A3667 (Vikhlinin et al. 2001b). In the latter case, the edge had been previously seen by ROSAT, but not with the same detail (Markevitch et al. 1999). Such edges may be expected in colliding clusters, which should drive shocks into the ICM. However, spectroscopic temperature measurements revealed these edges were not shocks, since the denser side of the discontinuity is the cooler one. Because of this difference, these edges were dubbed “cold fronts”.
An extended review of the properties and theory of cold fronts in clusters was first given by Markevitch & Vikhlinin (2007, hereafter MV07). Since that review, many more cold fronts have been discovered in galaxy clusters and similar objects, e.g., galaxy groups and elliptical galaxies. All of these systems are similar in the sense that in the context of this review all of them can be thought of as DM potentials (of masses ∼ 1013 − 1015 M⊙) filled with a hot plasma atmospheres (of temperatures T ∼ 106 − 108 K). Despite this large range in mass, for the remainder of the review we will refer to cold fronts in “clusters” as a shorthand.
Cosmological structure formation and hence the growth of galaxy clusters is still ongoing; thus, clusters are dynamic objects. The motion of gas within or between clusters and the presence of entropy gradients, both of which are conditions that are prevalent in clusters, provide the conditions for the formation of cold fronts. There are two classes of cold fronts, “remnant core” cold fronts and “sloshing” cold fronts, which were first distinguished by Tittley & Henriksen (2005). In the most general terms, remnant core cold fronts form when a galaxy, group, or cluster moves through a hotter ambient plasma and the resulting head wind strips off the outer layer of its atmosphere. This situation arises when a galaxy or group falls into a larger cluster, and even when two clusters are passing through each other. This process has also been described as “ram-pressure stripping” in the context of galaxies moving through the ICM of their host clusters (Gunn & Gott 1972, see also Roediger et al. 2015a and references therein). The formation of the cold front is also aided by the fact that the area-proportional drag force on the gas will decelerate the less dense gas of the core more, bringing the densest gas forward (see Figure 23 of MV07 for an illustration). These processes lead to an upstream contact discontinuity between the cooler, denser atmosphere of the infalling object and the hotter, less dense ambient gas. This leading edge is the remnant core cold front (Figure 1). It stretches from the stagnation point to the sides of the infalling atmosphere. Prominent examples are 1E0657-56 (Markevitch et al. 2002, the “Bullet Cluster”), the infalling elliptical galaxy NGC 1404 in the Fornax cluster (Dosaj et al. 2002, Scharf et al. 2005, Machacek et al. 2005, shown in Figure 1), and A3667 (Vikhlinin et al. 2001a, Vikhlinin et al. 2001b, Datta et al. 2014). In the literature, this type of cold front has also been referred to as a “merger” cold front.
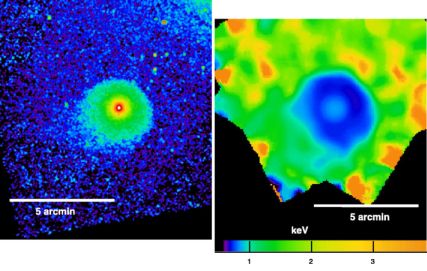 |
Figure 1.X-ray surface brightness (left) and spectroscopic temperature (right) maps for the elliptical galaxy NGC 1404, which is falling into the Fornax cluster. The galaxy moves towards the NW to the Fornax center. NGC 1404 is a classic example of a remnant core cold front, which stretches around the galaxy’s atmosphere from NE through NW to SW. Reproduced from Machacek et al. (2005). |
The second class of cold front, sloshing cold fronts, arises when some process offsets the bulk of the central ICM in a cluster from its hydrostatic equilibrium in the cluster potential. The ICM then slowly oscillates–or sloshes–around its hydrostatic equilibrium configuration (Markevitch et al. (2000), Tittley & Henriksen (2005), AM06). The variation of sloshing frequency with cluster radius leads to the formation of arc-shaped contact discontinuities staggered on opposite sides of the cluster core (Nulsen et al., in prep.). They are particularly visible if the cluster is of the “cool-core” variety, where the cluster has been relatively undisturbed for some time and the temperature in the center has slowly decreased via radiative cooling, causing the central density to go up to maintain hydrostatic equilibrium. In such clusters, the entropy profile is a steep function of radius, increasing the likelihood of producing contact discontinuities. Again, since the denser side of the contact discontinuity is the cooler one, the feature is a cold front. The required global perturbation of the ICM is achieved easily in a minor merger, i.e., the passage of a subcluster through the main cluster causes the ICM offset and subsequent sloshing (AM06), though Churazov et al. (2003) demonstrated that similar effects could be caused by the passage of a sufficiently strong shock. An off-center passage of a subcluster introduces some additional angular momentum into the ICM, resulting in sloshing cold fronts wrapped around the cluster core in a one-armed spiral-like pattern (Figure 2). The exact combination of linear sloshing, angular momentum, and viewing angle determines whether sloshing cold fronts are arranged in a clear spiral or rather in staggered arcs on opposite sides of the cluster core. Sloshing lasts for several Gyrs, such that the sloshing cluster can appear quite relaxed except for the sloshing signatures. Prominent examples of relaxed clusters with sloshing cold fronts are A2029 (Clarke et al. 2004, Paterno-Mahler et al. 2013, see Figure 2), Virgo (Simionescu et al. 2010, Werner et al. 2016), A2319 (Govoni et al. 2004, O’Hara et al. 2004), A2142 (Markevitch et al. 2000, Rossetti et al. 2013), and A1795 (Markevitch et al. 2001, Ehlert et al. 2015). By some estimates, sloshing cold fronts may exist in the cores of ∼1/2 - 2/3 of relaxed galaxy clusters (Markevitch et al. 2003, Ghizzardi et al. 2010).
 |
Figure 2. Sloshing in A2029. Left: X-ray surface brightness image of the central part of the cluster, showing sloshing cold fronts arranged in a spiral pattern. Right: Surface brightness residual image, highlighting the associated spiral-shaped surface brightness enhancement, and demonstrating the extent of the sloshing motions out to 400 kpc. Reproduced from Paterno-Mahler et al. (2013). |
1.2. Cold Fronts and ICM Plasma Physics
From their initial discovery, it was noted that cold fronts have special properties. First, all of the formation scenarios for cold fronts predict that there should be a velocity shear across the sharp interface. Simple perturbation analysis assuming pure inviscid hydrodynamics shows that such shear flow interfaces should develop Kelvin-Helmholtz instabilities (KHI) on a relatively short timescale (Chandrasekhar 1961), which is a few Myr for cold fronts in the ICM. Thus, a major question in relating cold fronts to ICM properties is whether or not cold fronts are stable or unstable to KHIs.
KHIs at a given shear flow interface can be suppressed in a variety of ways, by, e.g., a sufficiently strong magnetic field aligned with the shear flow interface (Chandrasekhar 1961, Vikhlinin & Markevitch 2002), or by a sufficient ICM viscosity (Roediger et al. 2013b). In the case of magnetic fields, KHIs are suppressed if the magnetic energy in the component of the field oriented parallel to the interface is roughly in excess of the kinetic energy in the shear flow (Landau & Lifshitz 1960, Vikhlinin & Markevitch 2002). Even if the field is too weak to completely suppress KHI, it may decrease its growth rate. Viscosity suppresses the growth of KHI below a certain length scale by damping out perturbations and smoothing out the velocity gradient at the interface layer by momentum diffusion (Kaiser et al. 2005, Junk et al. 2010, Roediger et al. 2013b), depending on the Reynolds number of the plasma. It should also be noted in this context that a small initial width of the cold front interface may be sufficient to suppress KHIs for a restricted range of angles along the surface (Churazov & Inogamov 2004), though this is not expected to be true for all observed cold fronts.
At remnant core cold fronts the shear flow has a specific structure along the cold front. The shear velocity is zero at the stagnation point, i.e., the most upstream point of the remnant core, and increases along the upstream edge towards the sides of the remnant core. Shear flows also arise along large stretches of sloshing cold fronts. For this reason, we should expect to see evidence of KHIs at the sides of remnant cores and along many sloshing cold fronts, or a washing out of the interface by the KHI. Nevertheless, many (though not all) cold fronts appear relatively undisturbed. This may indicate that the KHI are being suppressed, or that they are not as easy to recognize.
The second interesting property of cold fronts is the fact of the sharp interface itself. In many cases, the width of the interface is unresolved even by Chandra, and is often smaller than the electron and ion mean free paths. Diffusion of particles and heat should be very efficient across such an interface. In fact, the temperature and density of the gas on either side of the front imply that the thermal conduction timescale across the interface should be very fast, in which case the temperature and density gradients would be smeared out. Nevertheless, sharp cold front interfaces are present in many clusters, indicating that both heat flux and particle diffusion across the interface are both strongly suppressed.
These special properties of cold fronts provide an opportunity to use the combination of numerical simulations with X-ray observations to investigate the physical properties of the cluster plasma. This involves going beyond a simple HD description of the plasma to explicitly including the effects of magnetic fields and transport processes such as viscosity and thermal conduction. Simulations can provide predictions for observable signatures of specific ICM properties, e.g., the appearance or absence of KHIs in X-ray observations, or specific shapes for profiles of density and temperature across the fronts. By modeling ICM magnetic fields and transport processes explicitly, simulations may determine what plasma physics of the ICM is responsible for maintaining the smooth and sharp appearance of the cold fronts after their formation, and provide a more accurate description of the physics of the ICM. As more simulation works are incorporating these processes to understand their effect on ICM turbulence, their association with AGN feedback, and their effects on the thermal state of the cluster as a whole, it is vital to use detailed comparisions between simulations and observations to understand the nature of these processes in the ICM.
In this vein, a number of simulation works have been carried out over the past several years which incorporate various physics beyond pure HD in an attempt to explain the apparent long-term stability properties of cold fronts. These works have provided a number of key insights into ICM physics, but some questions still remain. The purpose of this paper is to review the results of these investigations. These simulations have approached the study of the ICM from the framework of a magnetized fluid, and so the focus of this review is on the constraints that can be placed on parameterized transport coefficients in this framework rather than detailed treatment of the underlying kinetics (see, however, Section 4.1.1 for some comments on the latter).
In Section 2, we review a number of key observations of nearby cold fronts. In Section 3, we review the simulations of cold fronts in clusters which have incorporated physics beyond HD. In Section 4 we describe the remaining open questions, and the role of future observations and simulations. Lastly, in Section 5 we provide a summary.