


A complete theory of the redshift must lead to results which meet the following requirements.
1. The redshift is analogous to a Doppler effect, i.e. Δλ / λ for a given nebula is a constant.
2. The apparent Doppler velocity is proportional to the distance r and amounts to 558 km per second per million parsecs.
3. There is no noticeable absorption and scattering of light in space, which may be associated with the redshift.
4. The definition of the optical images of nebulae is as good as is expected from the resolving power of the instruments. The distance of the objects apparently plays the role expected from geometric considerations.
5. The spectral types of nebulae are essentially independent of distance.
6. The great dispersion of the single values of the radial velocities of the nebulae of dense clusters must be explained in the context of the redshift.
7. The speed of light, on its long way from the nebula to us, is practically the same as the speed of light known to us from terrestrial measurements. This was found from aberration measurements on nebulae by Strömberg and van Biesbroeck.
8. A theory of the redshift, which at the same time does not provide an explanation of van Maanen's results, is at least unsatisfactory.
The facts stated above reflect the observational material up to a distance of about 150 million light years. For their explanation there are presently two general suggestions. The first includes all theories of cosmological character, which are based on the theory of relativity. The second one assumes an interaction of light with matter in the Universe.
In recent years a large number of attempts were made to explain the redshift on the basis of the theory of relativity. Some essential thoughts in this respect are the following.
The general theory of relativity has led to two views regarding the structure of space. The first one is represented by Einstein's quasi-spherical world, while de Sitter has derived the possibility of a hyperbolic space for the case of vanishingly small mass density.
While the geometry of Einstein's space does not lead directly to a redshift, it is necessarily linked with de Sitter's world. However, R. C. Tolman has shown that for the latter case Δλ / λ not only depends on the distance of the nebula, but also on its proper speed. It follows then that apart from the redshift one also has to expect blueshifts which would on average be smaller, but nevertheless of the same order of magnitude as the redshifts, which contradicts the observations. Therefore it was not possible to relate the redshift directly to the curvature of space.
A further important suggestion comes from Friedmann, Tolman, Lemaitre and Eddington, whose work suggests that a static space, according to the theory of relativity, is dynamically unstable, and therefore starts to contract or expand. This result was then interpreted by him [the author does not specify by WHOM] that the redshift would correspond to an actual expansion of the Universe. This proposal has since been discussed by many researchers. The easiest formulation was recently put forward by Einstein and de Sitter (A. Einstein and W. de Sitter, Proc. of the Nat. Acad. Sci., Vol. 18, p. 213, 1932). These two researchers have temporarily given up the existence of an overall curvature of space. The curvature of space was essentially a consequence of the introduction of a so-called cosmological constant Λ in Einstein's field equations, which is equivalent to postulate a repulsive force which compensates Newton's attraction for very large distances. This postulate was historically necessary to understand the existence of a non-vanishing mean density which would otherwise lead to infinite gravitational potentials in the limiting case of an infinite static space.
This latter difficulty however disappears automatically, if all matter in space moves away from, or approaches each other. Omitting the cosmological constant Λ and the mean curvature, the expansion of matter can then be related directly to the average density. An expansion of 500 km/s per million parsecs, according to Einstein and de Sitter, corresponds to a mean density ρ ≃ 10-28 g/cm3. Based on observations of self-luminous matter, Hubble estimates ρ ∼ 10-31 g/cm3. It is of course possible that luminous plus dark (cold) matter, taken together, result in a significantly higher density, and the value of ρ ∼ 10-28 g/cm3 does not therefore appear unreasonable. Einstein's theory further yields the following more precise relationship for the redshift
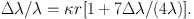 |
(3) |
This means that for large distances the redshift should increase stronger than linearly with the distance. On the basis of the previous observational material it is unfortunately not possible as yet to prove this important conclusion. The most recent observed values of Δλ / λ ∼ 1/7 for the largest distances are however large enough to expect considerable deviations (25%) from the linear relationship.
Theory also leads to certain conclusions regarding the distribution of brightness levels, number of nebulae, diameter, etc., as function of distance, which however have not yet been proven.
Up to now none of the cosmological theories has dealt with the problem of the large velocity dispersion in dense clusters, such as the Coma system.
B) Direct influence of existing matter in space on the frequency of light.
Several years ago I already attempted to consider various physical effects such as the Compton effect on stationary or moving electrons in outer space, the Raman effect, etc., to explain the redshift (F. Zwicky, Proc. Nat. Acad. Sci., Vol. 15, p. 773, 1929). It turned out that none of these can play an important role. When considering effects, which have their origin in an immediate spatial interaction between light and matter, it proves impossible to explain the transparency of intergalactic space.
However, I had then suggested another possible effect, which however will be barely observable on Earth, but for the existence of which some theoretical reasons can be put forward. According to relativity theory, each photon, or light quantum, of frequency ν can be assigned an inertial as well as gravitational of h ν / c2. Thus, there is an interaction (attraction) between light and matter. If the photon is emitted and absorbed at two different points, P1 and P2, respectively, with identical gravitational potentials, then, on the way from P1 to P2, the photon will lose a certain amount of linear momentum and will release it to matter. That photon becomes redder. This effect could be described as gravitational friction, and is caused essentially by the finite velocity of propagation of gravitational effects. Its strength depends on the mean density of matter, as well as on its distribution. In this case the redshift Δλ / λ not only depends on distance, but also on the the distribution of matter. Studies to prove these conclusions are in progress.
In conclusion it has to be said that none of the currently proposed theories is satisfactory. All have been developed on extremely hypothetical foundations, and none of these has allowed to uncover any new physical relationships.