4. SECONDARY INDICATORS

I refer here to distance estimators which are not directly derived from the stellar parallaxes as described in the previous sections. Most of the methods are very simple in essence, since one tries to compare the apparent luminosity of a source, how much radiant power is received on the Earth, to the true luminosity of the same source. Most of the problems with these techniques come from the selection of the standard candles, their reliable identification, the calibration of the method, the systematic effect affecting them, the extinction of light during its journey to the Earth and the assumptions regarding the true luminosity of the sources. The determination of distances farther than the range accessible to trigonometric parallaxes follows more a less a single model with the following steps:

• Identify a class of astronomical objects, bright enough to be seen at large distances
• Prove that they have a well defined luminosity to qualify as standard candles
• Measure the flux on the ground or from space around the Earth
• Find their distances to calibrate their luminosity
• Identify and select similar objects to find the distances of far-away galaxies
• Calibrate a new rung of the ladder with these new distances

Let L be the absolute luminosity of an astronomical source, that is to say the total rate of luminous energy production, and l the flux received on Earth per unit of surface. If we assume a propagation without loss of energy one has,

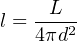(12)

where d is the distance between the star and the Earth. If l is measured and L is known or estimated from the star physical properties, then one can estimate the distance. In practice luminosities are expressed in a magnitude scale, and the distances in pc are related to the difference between the apparent (m) and absolute (M) magnitude as,

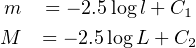(13) (14)

for the apparent and absolute magnitudes and with Eqs. 8 and 12,

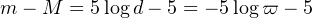(15)

with the convention that the absolute magnitude is the apparent magnitude the star would have if placed at 10 pc. Here ϖ is in arcsec, or equivalently the distance d = 1 / ϖ is in pc. Classically the magnitude difference m − M is called the distance modulus of the source. While rarely used for stars in our Galaxy it makes sense for clusters of stars at several kpc or Mpc such as a globular cluster, a dwarf galaxy surrounding the Milky way or a distant galaxy like Andromeda, as long as the source is resolved into stars. To illustrate this point the LMC (Large Magellanic Cloud), well visible in the southern sky, is located at about 50 kpc from the Milky Way. Therefore its distance modulus is 18.5 mag and a star similar to the Sun (M = 4.8) would have an apparent magnitude of 23.3, very faint for many of the telescopes in use today and not visible with Gaia. On the other hand, a classical Cepheid pulsating with a period of 4 days has M ≈ −3 and would be seen as a star of m = 15.5 in the LMC, rather easy to detect with a medium size telescope and an accurate target for Gaia.

The extinction along the path is probably the most serious issue near the galactic plane, which essentially amounts to saying that the radiant flux decreases faster than the inverse square law. If one has an absorption coefficient of Γ(l, b) in mag pc⁻¹ in the direction defined in galactic longitude l and galactic latitude b, Eq. 15 becomes for a source at distance d,

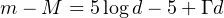(16)

For stars the extinction comes with a reddening, since dust scatters more efficiently the shorter wavelengths and the spectrum appears redder than what is expected for a star with known spectral type and luminosity class. There is a rather well defined relationship between the reddening (called colour excess) allowing one to make the corrections from stars observed at the same place and in the same direction.

4.2. Distances of clusters

This is the first level of photometric/spectroscopic-derived distance indicator relying on the absolute luminosity of stars and the technique providing the very first estimate of a distance for most of the stars in or out of the Galaxy. It is based on the location of stars on the Luminosity-colour diagram, usually referred to as the HR diagram named after E. Hertzsprung and H.N. Russel who discovered the feature independently around 1910. A diagram based on Hipparcos distances is shown in Fig. 4. Stars tend to fall only into certain regions of the diagram. The most prominent feature is the long concentration along a diagonal crossing the diagram from the top left to the lower right. This is the location of the main sequence where most of the stars lie during their hydrogen burning phase. In the lower-left there is a narrow line with white dwarfs, and, above the main sequence, several nearly horizontal lines with the subgiants, giants and supergiants, a state in the star life when core hydrogen is exhausted. The Sun is found on the main sequence at B − V = 0.66 and luminosity of 1 L_⊙ by definition. The spectrum of a star and its location in the diagram are highly correlated, to the extent that a solar analogue can be recognised from the absorption lines of its spectra from the depth or absence of characteristic lines such as Hydrogen, Calcium, Oxygen etc.

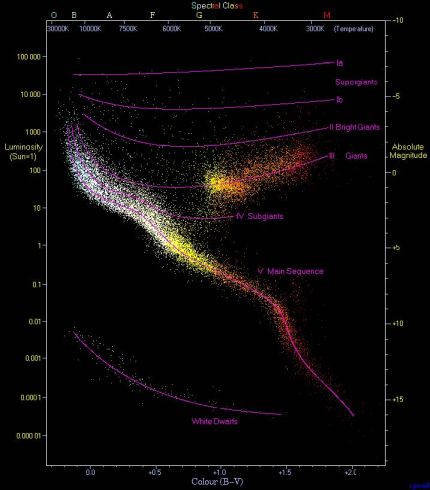Figure 4. An observational Hertzsprung-Russell diagram with 22,000 stars plotted from the Hipparcos Catalogue and 1,000 stars from the Gliese Catalogue of nearby stars.

However the same principle becomes much more efficient when applied to a cluster of stars [30], [31]. Observing a cluster like the Hyades or the Pleiades one may identify stars that belong to the cluster from their distances, kinematical parameters (they should have the same space velocity), chemical composition and then exclude field stars not related to the cluster. These stars are thought to have been formed from the same initial cloud at the same epoch. They have the same age and share a similar content of heavy elements. Being similar and at the same distance, their distribution in the HR diagram displays narrow sequences, with little scatter, at least for all the single stars. The difference between the absolute HR diagram and that of a cluster using apparent magnitude is just a vertical translation equal to the cluster distance modulus since the m−M is constant for all the members. By searching for the best fit between the main sequence of the cluster to a calibrated main sequence of the diagram one gets immediately the distance of the cluster. If extinction is significant, there is also a horizontal translation for the reddening. The calibration must be done beforehand on the closest clusters, like the Hyades from the trigonometric parallaxes or the kinematics of the whole cluster combining the tangent and radial motions. There are many complications in the details (ages, metallicity, He abundance, that differ from the reference cluster and displace the sequence), but the principles are as described and allow one to get distance estimates for most of the not too old open clusters found in the galactic plane where main sequence stars are visible. A solar-like star with V ≈ 4.7 is brighter than m_v = 20 up to d = 10 kpc without extinction. So the method extends the distances achievable without trigonometric parallaxes to few kpc in the Milky-Way.

4.3. Distances from the Cepheids

Using Cepheids as standard candle is the single most important distance indicator for extragalactic distances up to some 10s Mpc. Cepheids are supergiants stars of type F to K with regular brightness variation over periods ranging from 1 days to 50 days. The source of variability is well understood as an hydrodynamic instability causing the pulsation of the star which changes in size and surface temperature during the cycle. As supergiants Cepheids are intrinsically very bright and can be seen a very large distance, therefore detectable in external nearby galaxies. With a brightness of M ≈ −5, a star seen with apparent magnitude m = 22 is at a distance of (Eq. 15) 2.50 Mpc, three times as far as the Andromeda galaxy. During the first decade of the 1900s H. Leavitt studied variable stars in the LMC and SMC (Large and Small Magellanic clouds, two companion galaxies at 50 kpc from the Milky Way), and found about 50 Cepheids in the LMC. She rightly noticed that the period of variability was all the more longer as the star was bright. Moreover she showed that the mathematical law relating the apparent magnitude and the logarithm of the period was linear [32]. This was at once a major breakthrough in this field with far-reaching consequences for the understanding of the structure of the Universe. The early death of H. Leavitt deprived her of a likely Nobel Prize.

Given that these stars were all at the same distance, one could infer that the same relation held for the absolute magnitude, and provided the link between the period and the luminosity (the Period-Luminosity or PL relation) could be calibrated, one would know the distance of the host galaxy. Since then many calibrations have been published from census of galactic cepheids whose distances could be estimated by independent means. They are relatively rare sources and their number is limited to few thousands, although many new have been discovered by Gaia. The population is rather uniform and the basic assumption is that Cepheids in external galaxies behave like those found in the Milky Way. The Gaia DR2 variability set comprises 9675 stars classifieds as Cepheids, against only 599, mainly in the region of the LMC, in the DR1 [33]. This represents the first full-sky census of Cepheids and provides a flavour of Gaia potential to recover most of the Milky Way Cepheids [34], not hidden by dust clouds. A typical P-L law has the form, with the period P in days,

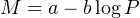(17)

or with a colour correction,

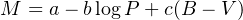(18)

where the most important parameter is the zero point coefficient a. The coefficients b and c are independent of the distance and result from the analysis of the light curves. Other colour indices that B−V are also used.

Until the advent of Gaia, the Cosmic distance scale rested primarily on the Cepheid calibration using the Hipparcos parallaxes with,

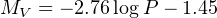(19)

with an estimated error in the range of 5−20%. Mention also the HST derived calibration [35]

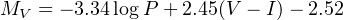(20)

Using Gaia DR1 and distances from the TGAS solution (Gaia combined with Hipparcos and Tycho), Clementini and collaborators [33] gave a new calibration for classical Cepheids in the V-band as,

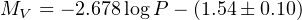(21)

See the paper for the details of the selection and the bias that may result. Taking the numbers as given one sees that a Cepheid with a period of 50 days, has a M_V magnitude of −6.1 and will be visible with the HST and without extinction at 2 Mpc. Similar calibrations have been also obtained for Population II Cepheids and the fainter, but much more frequent, RR Lyrae pulsating stars. The latter are much more common stars and are useful distance indicators for Globular clusters in the Milky Way halo up to 50 kpc. Calibration of the Galactic Cepheids from the Gaia DR2 is not yet completed, but a partial result for the Cepheids in the Magellanic clouds is shown in Fig. 5 from [34]. The colours code different types of Cepheids with slightly different Period-Luminosity relations. The plots are impressive by themselves for the number of sources, the resolution between the different populations and the small scatter around a visual linear fit. As the LMC / SMC distance modulus can be obtained by independent techniques, the curve can be transformed into absolute calibrations (with correction for the reddening) and compared to the Galactic Cepheids.

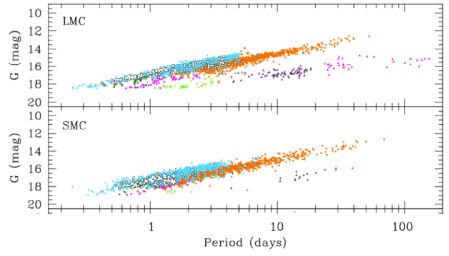Figure 5. Period-Luminosity relation in apparent G magnitude uncorrected from reddening in the LMC and SMC from the Gaia DR2 sample (adapted from [34]).

4.4. Towards cosmological distances

As detected so far, the spiral galaxy NGC 3370 contains the farthest Cepheids yet found at a distance of 29 Mpc. To reach distances where the Hubble flow becomes predominant other rungs are required for galaxies beyond 500 Mpc. So far the SNe Ia are the most relevant sources to be used as standard candles for the very large distances. SNe Ia result from the catastrophic instability of a binary white dwarf accreting material from its companion star and exploding when it reaches the Chandrasekahr limit. This well defined particular condition accounts for the relative uniformity of the observable properties, such as the light curve of the SN Ia and their maximum brightness. They are recognised from other SNs by the shape of their light curve after the maximum, their spectra and they constitute good standard candles with the peak luminosity M_V ≈ −19.5, corresponding in energy output to about 10⁹ L_⊙ [36]. They are seen in all types of galaxies with typically one event per galaxy every five centuries. Using Eq. 15, one sees that with the HST they can be seen at few Gpc distances, that is to say at the start of the cosmological distances. But this peak, standardised for different light curves, needs to be calibrated and again Cepheids are used for this purpose within galaxies at rather small distances of few Mpc as explained by Sandage and Tammann [37] in a classical paper.

A very important application of the Gaia DR2 Cepheids dealing with this topic has been reported in [38] with the combination of the HST photometry of 50 Cepheids located in galaxies at d < 50 Mpc where Supernovae Ia have been found and used to extend the distance scale to Gpc and constrain the Hubble constant. Basically this fills the necessary step to assess the absolute luminosity of SNe Ia within relatively nearby galaxies from a distance estimate of these galaxies based on another standard candle. Gaia Cepheids in the MW are the most coveted source to achieve this goal given their brightness (G < 12) and then their expected high parallax accuracy, about five times better than the HST astrometry. From the HST data and a previous Cepheid calibration using H₀ = 73.24 km s⁻¹ Mpc⁻¹ the authors have calculated the absolute magnitude of the Cepheids in the HST photometric system with the P−L relation,

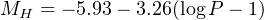(22)

The analysis done in [38] confirms the existence of a bias in Gaia DR2 parallaxes, but larger than the Gaia quoted value of −29 µas based on fainter quasars [28]. In the magnitude range of bright Cepheids they found −46 ± 6 µas instead. This has an implication for the Hubble constant, since the HST value is not in agreement with that determined from Planck cosmic microwave background (CMB) data which yields H₀ = 66.93 ± 0.62 km s⁻¹ Mpc⁻¹. However no such tension appears in [39] if we extend the DR2 bias found for the quasars to the bright Cepheids and the Planck value of H₀. The issue is not solved yet but is just mentioned to show that even with the best tools in the hands of astronomer, as Gaia and HST are, the metrology is never simple and extreme care must be exercised everywhere. With Gaia parallaxes and their sheer number, a new page just opens up and new papers are expected in the coming years discussing and questioning the cosmic distance scale established with different techniques.