10. THE LM/DM UNIVERSAL PROPERTIES

One could resume the state of the art of the issue of “DM in galaxies”, by stressing the unexpected scheme shown by the distributions of the dark and luminous matter in galaxies: halo masses, stellar component/baryonic masses, central densities, luminosities, DM density length scales, half-light radii, and galaxy morphologies are all engaged in a series of relationships, difficult to be understood in a physical sense. However, since the concurrent view argues that “galaxy formation is a complex phenomenon which could account for the apparently inexplicable observational scenario”, we stress that the above is far beyond a list of galaxy relationships, but a coherent pattern that can help us in the search of the unknown dark particle.

In disk systems (dwarf disks, low surface brightness galaxies and spirals) when the values of their structural quantities are expressed in physical units, the stellar component forms a family ruled by three parameters: the disk length-scale R_D and the magnitude (e.g., M_I) and the stellar disk concentration C_⋆. In the same systems, also the dark component is represented by a family ruled by three parameters: the core radius r₀, the central density ρ₀ and C_DM the DM concentration. The two families are closely and mysteriously related: the entanglement is so deep that it is difficult to understand which rules which.

Remarkably, the situation much simplifies when we express the circular velocity V(r) ¹² in the double-normalized form: V(r / R_opt) / V(R_opt) The profiles of the RCs emerge as a function of just one parameter, at choice among the above six, plus V_opt, M_vir and the angular momentum for unit mass j (see Lapi et al. 2018). Remarkably, this occurs independently on whether a galaxy is dark matter or luminous matter dominated for R < R_opt. The emerging evidence is that structural quantities deeply rooted in the luminous sector, like the disk length scales, tightly correlate with structural quantities deeply rooted in the dark sector, like the DM halo core radii.

Let us conclude this section noticing that this scenario is, instead, still under investigation in spheroidal galaxies.

10.1 The cored distributions of dark matter halos around galaxies

The current situation is the following: a) in disk systems of all morphologies and luminosities there is strong evidence that the DM halo density profile is very shallow out to the edge of the stellar distribution R_opt b) in dwarf spheroidals and in ellipticals, also due to the intrinsic difficulty in these systems to disentangle the actual kinematics from the biased one, the situation is less clear, although, also in these objects, there are several claims of cored DM halo density profiles. In conclusion, the claim that DM around galaxies have a density distribution well represented by the cored B-URC profile is bald, but I believe correct.

The most intriguing aspect of the DM in galaxies is not that they all possess a universal density profile, but that, this latter comes with a couple of very unexpected properties. The analysis of rotation curves, dispersion velocities, and weak-lensing data of large samples of dSphs, dwarf irregulars, spirals, and elliptical galaxies, found that the product of the DM core radius r₀ with the DM central density ρ₀ is nearly constant in galaxies, i.e., independent of their luminosity (Donato et al. 2009; see also Donato et al. 2004). This result, pioneered by Kormendy and Freeman (2004), is obtained in Donato et al. (2009) from the mass models derived from 1) about 1000 coadded RCs of spirals, 2) hundredths individual RCs of normal spirals of late and early types 3) galaxy-galaxy weak lensing signals 4) the inner kinematics of Local Group dwarf spheroidals 5) the RCs of 36 dd and 72 LSBs (see Di Paolo and Salucci 2018). The relationship reads (see Fig. 27).

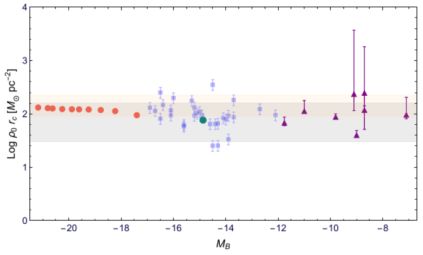Figure 27. (Central DM halo density) × (halo core radius) as a function of a galaxy magnitude. Legenda: rc ≡ r0. Data are from the URC of spirals (red circles), the scaling relation in Donato et al. (2009) (orange area), the Milky Way dSphs (purple triangles) Salucci et al. (2012), the dds (blue squares) Karukes and Salucci (2017). Also shown the relationship by Burkert (2015): ρ0 rc = 75−45+85 M⊙ pc−2 (grey area) (see also Spano et al. 2008). Image reproduced with permission from Karukes and Salucci (2017), copyright by the authors.

At a higher level there is the correlation between the compactness of the stellar disks and that of the DM halos in dark matter dominated dds and LSBs (see Fig. 28 and the related caption). It is legitimate to interpret all this as an evidence of the dark and luminous worlds conjuring in galaxies.

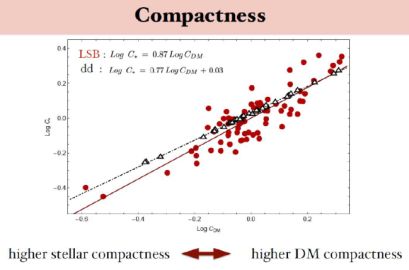Figure 28. The relationships between the compactness of the stellar disks and that of DM halos in dd and LSB galaxies (Karukes and Salucci 2017, Di Paolo and Salucci 2018). Let us set: M and S for a generic galaxy mass and size. We perform, in a sample of galaxies, the regression log S = a + b log M. For each galaxy i of the sample the compactness log Ci is defined by log Ci = −log(Si) + a + b log Mi. Here, for the luminous matter: M ≡ M⋆, S ≡ RD and Ci ≡ C⋆ ; for the DM: M ≡ Mvir, S ≡ r0 and Ci ≡ CDM.

The relationship between the halo mass and the stellar mass located at its center is an important and well investigated one. It is well known that the mass fraction DM / LM as a function of the halo mass follows a characteristic U-shaped curve (Wolf et al. 2010, Moster et al. 2010) for which M_vir / M_⋆ is minimized at the halo mass M_vir,break ≈ 3 × 10¹¹ M_⊙ and rises at both lower and higher masses. According to the URC, the value of M_vir,break corresponds to M_star,break ∼ 1.2 × 10¹⁰ M_⊙ and to L_break ∼ 5 × 10⁹ L_⊙ in the r*-band luminosity (see also Lapi et al. 2018). Outliers of this relationship do exist (Beasley et al. 2016), however, here we do not further enter this topic certainly related to the “galaxy formation process”.

Therefore, the empirical scenario includes six quantities that define a galaxy: three in the dark sector (halo mass and core radius and DM halo compactness) and three in the luminous sector (stellar/baryonic mass, half-light radius and stellar disk compactness). They all relate each other but, while some of these relationships lay in the heart of the DM mystery, others, instead, lay in the ball-park of the galaxy formation and evolution process.

10.2. The dark-luminous matter coupling 2.0

In spirals, dwarf disks and LSBs there are extraordinary multiple connections between the dark and the luminous components. This occurs over many orders of magnitudes in halo masses and over the whole ranges of galaxies morphology and luminosity. The “standard” explanation relates to a dynamical evolution of the galaxies, in particular, of their DM halo densities, caused by powerful baryonic feedbacks. Although this scenario is far than being rejected, it seems, however, unable to cope with the intriguing wealth of correlations between quantities deep-rooted in opposite dark/luminous worlds that we have presented in this review. More in detail, while we cannot completely rule out the possibility that astrophysical phenomena can be responsible for the above intriguing scenario, on the other hand, what emerges in galaxies allow us to propose a shift of paradigm, according to which, the nature of dark matter is not given to us by convincing theoretical arguments, but must be searched in the various properties of the DM halos and stellar disks.

In Salucci and Turini (2017), it is argued that these new ideas can be justified also by some direct hint: in spirals the DM pseudo pressure ρ_DM(r) V²(r) reaches a maximum value always close to the core radius r₀ and this maximum takes the same value in all objects, no matter the galaxy mass. Moreover, at r = r₀ in all disk systems, the quantity ρ(r) ρ_⋆(r) takes the same value. We notice that this density product is proportional to the interaction probability between the , the luminous and the dark matter. This is hardly a coincidence, in that, the quantity like K_SA = ρ_DM²(r) , which is proportional to the self interaction of the DM component, is largely varying in galaxies and among galaxies. One can speculate that the structure of the inner parts of the galaxies is driven by a direct interaction between dark and luminous components on timescales of the order of the age of the Universe. The DM central cusp, outcome of the proto-halo virialization, as time goes by, gets progressively eaten up/absorbed by the dominant luminous component. The interaction, then, flattens the density of DM and drops the pressure towards the center of the galaxy and it is likely to leave in inheritance the above galaxy relationships.

¹² V(r) = (r dΦ / dr)^1/2 with Φ the total gravitational potential. Back.